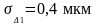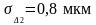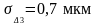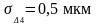- •200106 «Информационно-измерительная техника и технологии»
- •Введение
- •1.2. Сигналы
- •1.3. Преобразование измерительных сигналов
- •1.4. Спектр периодических сигналов
- •1.5. Модуляция
- •1.5.1. Амплитудная модуляция
- •1.5.2. Частотная модуляция
- •1.5.3. Фазовая модуляция
- •1.5.4. Двукратные виды модуляции
- •1.6. Квантование
- •1.6.1. Квантование по уровню
- •1.6.2. Квантование по времени
- •1.6.3. Квантование по уровню и времени
- •1.7. Кодирование
- •1.7.1. Цифровые коды
- •1.7.2. Помехи
- •1.8. Модель канала
- •Раздел 2 измерительные каналы и их разделение
- •2.1. Канал связи и его характеристики
- •2.2. Согласование канала с источником информации
- •2.3. Линии связи для передачи измерительной информации
- •2.4. Структуры линий связи
- •2.5. Многоканальные системы для передачи измерительной информации
- •2.6. Погрешность систем с частотным разделением каналов
- •2.7. Погрешности систем с временным разделением каналов
- •Раздел 3 принципы обработки данных
- •3.1. Виды погрешностей
- •3.2. Обработка результатов измерений. Оценки измеряемой величины
- •3.3. Обработка результатов прямых равноточных измерений
- •3.4. Обработка результатов косвенных измерений
- •3.5. Обработка результатов совместных измерений
- •3.6. Обработка результатов неравноточных измерений
- •3.7. Проверка статистических гипотез
- •3.7.1. Проверка соответствия гипотезы и экспериментальных данных
- •3.7.2. Исключение резко отклоняющихся значений
- •3.8. Построение эмпирических распределений
- •3.9. Критерии согласия
- •3.9.1. Критерий согласия Пирсона
- •3.9.2. Критерий согласия Колмогорова
- •Раздел 4 планирование многофакторного эксперимента
- •4.1. Задачи планирования эксперимента
- •4.2. Пассивные эксперименты
- •4.3. Дисперсионный анализ
- •4.4. Регрессионный анализ
- •4.5. Активный эксперимент
- •4.6. Полный факторный эксперимент
- •4.7. Дробный факторный эксперимент
- •4.8. Устранение влияния временного дрейфа
- •4.9. Проведение факторного эксперимента и обработка его результатов
- •4.10. Оптимизация
- •4.11. Рандомизация
- •Раздел 5 введение в алгоритмическую теорию измерений
- •5.1. Вводные замечания
- •5.2. Развитие понятий числа и измерения величин
- •5.3. Теория шкал и алгоритмические измерения
- •5.4. Алгоритмы измерения в номинальной шкале, аддитивной и порядка
- •5.5. Моделирование цифровых алгоритмических измерений
- •5.6. Эквивалентность между фильтрацией и алгоритмическим измерением
- •5.7. Моделирование сигналов. Дискретизация
- •5.7.1. Модели дискретизации аналогового сигнала
- •5.7.2. Дискретизация с усреднением
- •5.7.3. Дискретизация сигналов конечной длительности
- •5.8. Цифровое представление информации
- •5.9. Системы счисления с иррациональными основаниями
- •5.9.1. Золотая пропорция
- •5.9.2. Числа Фибоначчи
- •5.9.4. Код золотой p-пропорции
- •5.10. Общий алгоритм метрологического кодирования
- •5.10.1. Алгоритм Стахова
- •5.10.2.Фибоначчиевы алгоритмы цифрового метрологического кодирования
- •Раздел 6 введение в информационную теорию измерений
- •6.1. Основные положения теории информации
- •6.1.1. Энтропия
- •6.1.2. Единицы измерения энтропии
- •6.1.3. Условная энтропия (энтропия помехи)
- •6.1.4. Суммирование нескольких погрешностей
- •6.1.5. Явление «краевой эффект». Приближенность информационных оценок каналов передачи информации
- •6.1.6. Основные положения теории информации для характеристики процесса измерения
- •6.2. Сущность измерения
- •6.2.1. Понятие натурального ряда однородных величин
- •6.2.2. Понятие шкалы реперов измеряемой величины
- •6.2.3. Измерение как сужение интервала неопределенности
- •6.3. Измерительные преобразования, функциональные шкалы, единицы измеряемой величины
- •6.3.1. Функциональная шкала измеряемой величины
- •6.3.2. Понятие единицы измерения
- •6.3.3. Метод построения измерительных устройств
- •6.4. Измерительные преобразования и преобразователи
- •6.5. Энтропийное значение погрешности
- •6.5.1. Математическое определение энтропийного значения погрешности
- •6.5.2. Эффективное значение погрешности
- •6.6. Сравнение энтропийного и среднеквадратического значений погрешности для плавных симметричных одномодальных законов распределения погрешностей
- •6.7. Энтропийное значение погрешности – основной критерий точности приборов и измерений
- •6.8. Определение энтропийного значения погрешности на практике
- •6.9. Суммирование погрешностей измерительных устройств
- •6.10. Статистическое суммирование погрешностей при наличии корреляции
- •6.11. Энтропийное значение результирующей погрешности
- •6.12. Суммирование погрешностей с равномерными законами распределения вероятностей
- •6.13. Суммирование погрешностей при равномерном и нормальном законах распределения составляющих результирующей погрешности
- •6.14. Суммирование погрешностей при произвольной степени корреляции и произвольных законах распределения вероятностей составляющих результирующей погрешности
- •И объемов (n) выборок
- •Интервала
- •Оглавление
3.6. Обработка результатов неравноточных измерений
В практике измерений встречаются ситуации, когда оценки измеряемых величин должны быть получены путем обработки результатов измерений, выполненных в различных условиях: различными экспериментаторами, разными методами, с использованием различных средств измерений. При этом часто нет оснований для того, чтобы отдать исключительное предпочтение какой-либо одной группе результатов, а остальные отбросить как не заслуживающие доверия. В то же время степень доверия тем или иным результатам может быть различна, например, из-за различия в точностях примененных средств измерений. Таким образом, каждому используемому результату или группе результатов измерений необходимо приписать некоторый вес, характеризующий степень доверия этим результатам.
Веса могут устанавливаться субъективно, на основе мнения экспериментатора или группы специалистов-экспертов, или объективно, на основе имеющихся данных о степени неопределенности тех или иных результатов. В последнем случае веса обычно устанавливают обратно пропорционально дисперсиям соответствующих погрешностей результатов измерений:
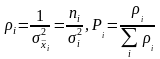 (3.6.1)
(3.6.1)
где
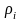 – вес, соответствующий i-му
результату или i-и
группе результатов;
– вес, соответствующий i-му
результату или i-и
группе результатов;
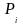 –
вес, соответствующий отдельному ряду
измерений;
–
вес, соответствующий отдельному ряду
измерений;
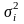 – дисперсия соответствующих результатов
измерений;
– дисперсия соответствующих результатов
измерений;
 – const
(например количество измерений в группе).
– const
(например количество измерений в группе).
Величина
с может
быть установлена произвольно. Для
удобства вычислений ее выбирают так,
чтобы все
были целыми числами, либо так, чтобы
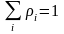 .
Так как веса
– безразмерные числа, то константа с
имеет
размерность дисперсии, поэтому далее
будем обозначать ее
.
Тогда при установленных весах
дисперсия i-го
результата запишется в виде
.
Так как веса
– безразмерные числа, то константа с
имеет
размерность дисперсии, поэтому далее
будем обозначать ее
.
Тогда при установленных весах
дисперсия i-го
результата запишется в виде
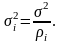 (3.6.2)
(3.6.2)
Рассмотрим задачу
обработки результатов прямых неравноточных
измерений. Пусть даны результаты
неравноточных измерений
 ,
которые
независимы и имеют нормальное распределение
с математическим ожиданием а
и дисперсиями
,
которые
независимы и имеют нормальное распределение
с математическим ожиданием а
и дисперсиями
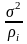 ,
причем веса
известны. Найдем оценки измеряемой
величины а
и дисперсии
2.
,
причем веса
известны. Найдем оценки измеряемой
величины а
и дисперсии
2.
Плотность распределения любого результата xi
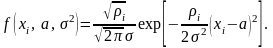 (3.6.3)
(3.6.3)
Соответствующая функция правдоподобия для всей совокупности результатов xi имеет вид:
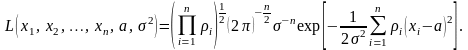 (3.6.4)
(3.6.4)
Максимум функции правдоподобия достигается при выполнении условия
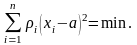 (3.6.5)
(3.6.5)
Выражение (3.6.5) является условием метода наименьших квадратов при неравноточных измерениях. Из (3.6.5) следует
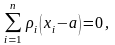 (3.6.6)
(3.6.6)
откуда
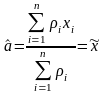 (3.6.7)
(3.6.7)
или, учитывая, что весовой коэффициент обратно пропорционален дисперсии
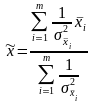 . (3.6.8)
. (3.6.8)
Оценка
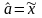 называется средней взвешенной оценкой.
называется средней взвешенной оценкой.
Вычислим
математическое ожидание и дисперсию
оценки
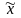 :
:
 ; (3.6.9)
; (3.6.9)
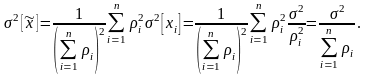 (3.6.10)
(3.6.10)
Таким образом, оценка является несмещенной, а ее вес равен сумме весов усредняемых результатов.
Для вычисления оценки дисперсии 2 прологарифмируем функцию правдоподобия (3.6.4):
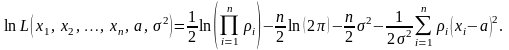 (3.6.11)
(3.6.11)
Найдем оценку дисперсии 2 из условия максимума функции (3.6.11):
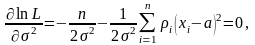 (3.6.12)
(3.6.12)
откуда
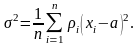 (3.6.13)
(3.6.13)
Используя вместо а оценку х, получаем
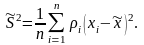 (3.6.14)
(3.6.14)
Оценка
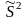 является смещенной, а для ликвидации
этой смещенности необходимо ввести
поправочный множитель
является смещенной, а для ликвидации
этой смещенности необходимо ввести
поправочный множитель
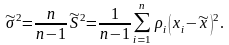 (3.6.15)
(3.6.15)
При
получении интервальных оценок для
значений величин а
и 2
можно
принять, что величина х
распределена
нормально с математическим ожиданием
а и
дисперсией
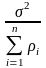 .
Отсюда следует, что дробь
.
Отсюда следует, что дробь
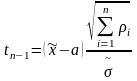
будет распределена по закону Стьюдента с п– 1 степенями свободы. Аналогично дробь
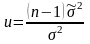
распределена по закону 2 с n-1 степенями свободы. В остальном правила построения соответствующих доверительных интервалов аналогичны описанным в § 3.3.
Пример 3.6.1. Тремя коллективами экспериментаторов с помощью различных методов были получены следующие значения ускорения свободного падения: g1 = (981,9190 ± 0,0014) см с-2; g2 = (981,9215 ± 0,0016) см с-2; g3 = (981,923 ± 0,002) см с-2. Определить значение ускорения свободного падения.
Решение. Весовые коэффициенты отдельных рядов измерений вычислим по (3.6.1):
 ;
;
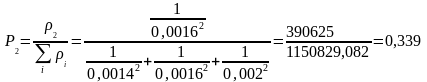 ;
;
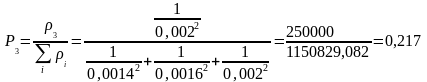 .
.
Средняя взвешенная оценка в соответствии с (3.6.7) равна:
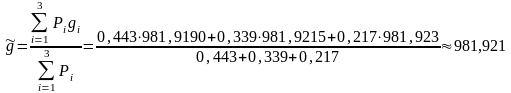 ,
,
его среднее квадратическое отклонение, исходя из (3.6.1) можно определить как
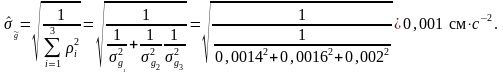
Пример 3.6.2. Измерения образцовой меры длины, выполненные приборами разной точности, дали результаты, приведенные в таблице 3.6.1.
Определить среднее взвешенное отклонение размера от номинального значения и оценку среднего квадратического отклонения среднего взвешенного.
Решение. Преобразуем выражение (3.6.8), так как в задаче приведены средние квадратические результатов измерений а не средних сначений результатов измерений:
Таблица 3.6.1
Порядковый номер измерения |
Отклонение от
номинального размера l
и среднее квадратическое отклонение
результатов измерения
характерное для данного прибора, мкм |
|||
Вертикальный оптиметр,
|
Машина типа Цейсс,
|
Машина типа Сип,
|
Миниметр с ценой деления 1 мкм,
|
|
1 |
11,3 |
10,8 |
9,8 |
10,4 |
2 |
– |
11,1 |
10,7 |
11,2 |
3 |
– |
10,9 |
– |
10,1 |
4 |
– |
– |
– |
9,9 |
Номера групп измерений i = 1, 2, …, m |
i = 1 |
i = 2 |
i = 3 |
i = 4 |
Число измерений в группе ni |
n1 = 1 |
n2 = 3 |
n3 = 2 |
n4 = 4 |
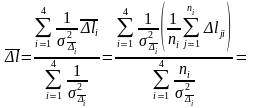
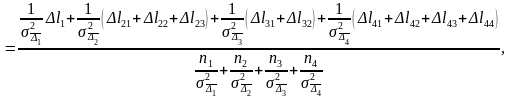
где i – порядковый номер группы измерений от 1 до m; – число измерений в i-ой группе; j – порядковый номер измерения в i-й группе. Подставляя экспериментальные значения из табл. 3.6.1, получим
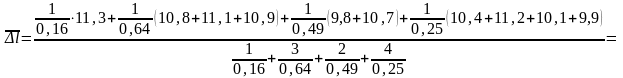

Среднее квадратическое отклонение, исходя из (3.6.1) можно определить как
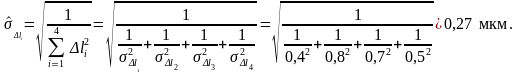

 ,
,