4.4. Регрессионный анализ

Регрессионный анализ служит для нахождения по результатам эксперимента связи выходной характеристики устройства (процесса) с факторами, которые влияют на эту характеристику.

В качестве модели регрессии используются пря­мая линия или различные математические кривые: участ­ки параболы, гиперболы, экспоненты и т.п. Эксперимен­тальные данные могут быть аппроксимированы с требуемой точностью функциями различного вида, поэтому выбор ви­да функции не может быть формализован. Его осуществля­ет экспериментатор, руководствуясь следующими соображе­ниями: регрессионная модель должна быть простой, удоб­ной для дальнейшего использования и адекватной. Под адекватностью модели понимают ее способность предска­зывать с требуемой точностью значения у в некоторой об­ласти значений х. Вид модели выбирают таким образом, чтобы при обязательном соблюдении адекватности она была наиболее простой и удобной.

На практике во многих случаях приближенно («на глаз») графически проводят линию, описывающую зависи­мость среднего значения у от х, и, исходя из ее вида, вы­бирают регрессионную модель.

Очень часто зависимость y от x можно принять линейной (линейная модель):

(4.4.1)

Для упрощения способов нахождения коэффициентов регрессии важно принять следующие допущения:

1. результаты наблюдений у₁, у₂, ..., у_i, ..., у_п (где п – число наблюдений над величиной y) представляют собой независимые, нормально распределенные случайные величины;

2. дисперсии D(y_i) равны друг другу, или пропорциональны какой-то известной функции Ф(y);

3. переменные х₁, x₂, ..., x_k являются независимыми и изме­ряются с пренебрежимо малой погрешностью по сравнению с вели­чиной [y_i].

Методы вычисления коэффициентов регрессии базируются обычно на аппарате матричного исчисления; при этом в наиболее громоздких случаях используются стандартные программы на ЭВМ.

Результаты эксперимента записываются в виде матрицы наблю­давшихся значений:

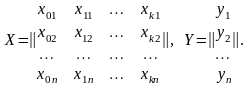(4.4.2)

По этим данным можно найти точечные оценки коэффициентов регрессии. Для этого, используя метод наименьших квадратов, со­ставляют n несовместных уравнений:

(4.4.3)

Из этой системы уравнений можно определить (k + 1) коэффициен­тов регрессии. Решение делают в матричной форме. Всю систему уравнений записывают в матричной форме в виде ХA = Y, где:

(4.4.4)

Матрицу при этом определяют из уравнения

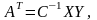(4.4.5)

где – транспонированная матрица A; – обратная матрица произведения С = Х^ТХ, равная = (Х^ТХ)^-1. В соответствии с этим уравнением для получения матрицы A (а значит, и всех оце­нок коэффициентов регрессии) необходимо произвести ряд преоб­разований, которые хотя и являются стандартными в матричном исчислении, но в общем виде не наглядны, поэтому ход таких вы­числений представлен ниже на конкретном числовом примере.

Пример 4.4.1. Результаты эксперимента представлены в таблице.

N	x1	x2	y	N	x1	x2	y	N	x1	x2	y
1	0	0	10	4	1	0	14	7	2	2	40
2	0	1	17	5	2	0	18	8	0	-1	3
3	0	2	20	6	1	1	24	9	-1	-1	3

Число факторов k = 2. Количество опытов п = 9.

Необходимо провести регрессионный анализ, определив значения коэф­фициентов регрессии.

Решение. Пусть полином для функции у (модель) линейный:

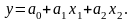
Составим матрицу X и транспонированную матрицу:

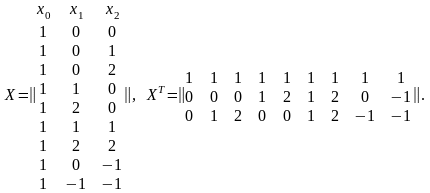
Найдем произведение , складывая почленно произведения элементов строк и столбцов X:

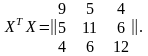
Для вычисления обратной матрицы (Х^ТХ)^–1 найдем сначала определитель матрицы Х^ТХ:

 = 9 (11  12 – 6  6) – 5 (5  12 – 4  6) + 4 (5  6 – 4  11) = 628.

Матрицу (Х^ТХ)^–1 составим из определителя  и дополнений матрицы Х^ТХ:

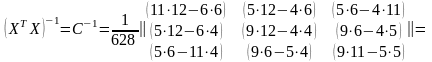
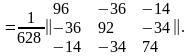
Далее запишем матрицу Y и найдем произведение Х^ТY:

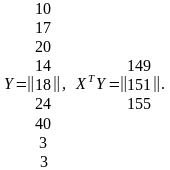
Далее

Таким образом: a₀ = 10,65; a₁ = 5,2; a₂= 6,8, и уравнение регрессии по­лучает следующий конкретный вид:

y = 10,65 + 5,2 х₁ + 6,8 х₂.

Далее необходимо проихвести проверку адекват­ности полученного уравнения опытным данным. Это необходимо, так как вид зависимости был заранее неизвестен и выбирался наиболее простой.

Адекватность проверяют обычно по критерию Фишера F:

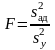. (4.4.6)

Оценку дисперсий и производят по формулам

, (4.4.7)

где – измеренное значение величины y, – расчетное значение величины y, вычисленное по полу­ченному уравнению регрессии при подстановке в него опытных значений x_j; k – количество коэффициентов в уравнении регрессии; п – количество опытов; п – k = f – число степеней свободы,

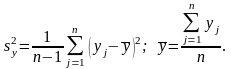(4.4.8)

Критерий F (таблица П. 4. «Значения (верхние значения) и (нижние значения) для различных степеней свободы f₁ и f₂») позволяет сравнить общий разброс относительно линии регрессии с разбросом в точке. Зада­вая уровень значимости q (обычно q выбирают равным 0,05), по таб­лице Фишера для (п – k) степеней свободы находят значение кри­терия F. Если оно больше вычисленного выше, то полученная в ви­де уравнения регрессии модель адекватна результатам эксперимента, если же нет – то требуется выбрать другой, более сложный вид уравнения. Однако здесь необходимо соблюдать условие, чтобы чис­ло опытов было не меньше числа оцениваемых коэффициентов.

Если число опытов в каждой точке (т.е. при каждом сочетании значений факторов) больше единицы и различно, то находят по формуле:

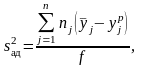(4.4.9)

где n_j – число параллельных (повторных) опытов в j-й строке мат­рицы; 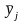 – среднее арифметическое из n_j параллельных опытов. Из этой формулы видно, что различие между экспериментальным и расчетным значениями имеет тем большее значение, чем больше число повторных опытов.

Следующий этап анализа состоит в проверке значимости коэф­фициентов. Его можно осуществлять двумя равноценными способами: проверкой по t-критерию Стьюдента или построением доверитель­ного интервала. Если опытные данные получены в результате пол­ного факторного эксперимента или регулярных дробных реплик, то доверительные интервалы для всех коэффициентов (в том числе и эффектов взаимодействия) равны друг другу.

На этом этапе найдем сначала дисперсию коэффициента регрес­сии s² (a_j) по формуле:

(4.4.10)

Дисперсии всех коэффициентов равны друг другу, так как они за­висят только от погрешности измерений и числа опытов. Довери­тельный интервал для j-го коэффициента определяется по формуле

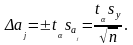(4.4.11)

Здесь – квантиль распределения Стьюдента при числе степеней свободы, с которыми определялась дисперсия для вероятности, равной выбранному уровню значимости.

Коэффициент значим, если его абсолютная величина больше до­верительного интервала, т.е. если его среднее влияние на у боль­ше, чем разбросы за счет неточности модели и «мешающих» факторов.

Очень часто в качестве модели используют степен­ной полином вида

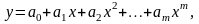(4.4.12)

где а₁, а₂, ..., а_т – параметры модели.

Такая модель при правильном выборе степени полино­ма позволяет с любой необходимой точностью аппроксими­ровать любую истинную регрессионную зависимость. Достоинст­вом модели является также то, что функция линейна отно­сительно неизвестных параметров a₀, а₁, а₂, ..., а_m, что упро­щает обработку наблюдений. В данном случае вопрос выбора вида модели сводится к выбору порядка m по­линома.

После выбора вида регрессионной модели вычисляют ее параметры. Для модели (4.4.12) необходимо получить оценки параметров a₀, а₁, а₂, ..., а_m, что можно сделать на ос­нове метода, рассмотренного в § 3.5.

Предположим, что y_i (i = 1, 2, ..., п) – это значения выходного параметра объекта, определяемые регрессионной зависимостью от x_i, а l_i – соответствующие результаты из­мерений выходного параметра. Разность в об­щем случае отлична от нуля из-за наличия погрешностей измерения и возмущающих воздействий на объект исследо­вания.

Здесь и далее считаем, что отклонение адди­тивно (не зависит от значения у) и распределено нормаль­но с нулевым математическим ожиданием.

Для регрессионной модели (4.4.12) запишем систему нормальных уравнений:

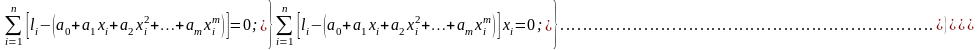(4.4.13)

Преобразовав (4.4.13) к стандартному виду, получим:

(4.4.15)

В результате решения системы уравнений (4.4.15), линей­ных относительно искомых параметров a₀, а₁, а₂, ..., а_m, получим их оценки

,

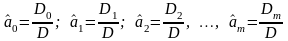где

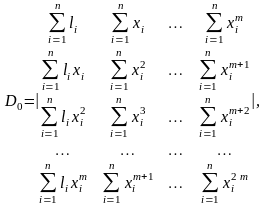
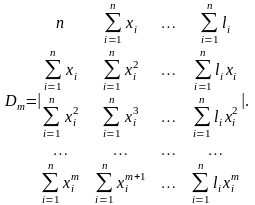
Бывает так, что модель нелинейной регрессионной зависимости целесообразно искать в виде функции, отличной от степен­ного полинома (4.4.12), например, в виде

(4.4.16)

который содержит два неизвестных параметра а и b. При­менение полинома (4.4.12) при той же точности модели может потребовать более высокого порядка полинома, что повышает трудоемкость вычислений.

Однако использование таких нелинейных (относительно параметров) функций осложняет вычисление их параметров. В некоторых частных случаях решение задачи упро­щается, если искусственно преобразовать нелинейную мо­дель в линейную. Например, для функции (4.3.16) необходимо сделать замену переменной вида Тогда получим линейную модель

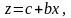(4.4.17)

где .

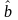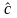При этом необходимо соответственно преобразовать ис­ходные экспериментальные данные – вычислить совокуп­ность значений z. Затем методом наименьших квадратов находят оценки и параметров линейной модели (4.4.17) и осуществляют обратный переход к нелинейной модели (4.4.16).