3.4. Обработка результатов косвенных измерений

В результате косвенных измерений определяется значе­ние физической величины, функционально связанной с другими физическими величинами, значения которых рав­ны :

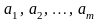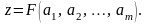(3.4.1)

Пусть каждая из величин 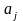(j = 1, 2, ..., т) измерена с погрешностью 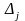. Необходимо оценить значение погрешно­сти z результата косвенного измерения.

Рассматривая z как функцию т переменных , запи­шем ее полный дифференциал:

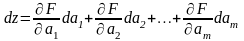(3.4.2)

или

. (3.4.3)

Положив, что погрешности измерений достаточно малы, заменим в (3.4.3) дифференциалы соответствующими при­ращениями:

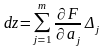. (3.4.4)

Каждое слагаемое (3.4.4) вида 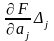представля­ет собой частную погрешность результата косвенного изме­рения, вызванную погрешностью определения величины . Частные производные 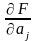носят название коэффициентов влияния соответствующих погрешностей.

Формула (3.4.4) является приближенной, так как учи­тывает только линейную часть приращения функции, одна­ко в большинстве практических случаев она обеспечивает удовлетворительную точность оценки погрешностей резуль­татов косвенных измерений.

Если известны систематические погрешности резуль­татов прямых измерений величин , то по (3.4.4) вычисля­ется систематическая погрешность z результатов косвен­ных измерений. При этом если частные погрешности имеют разные знаки, то происходит частичная компенсация систематических погрешностей.

Эта же формула может быть использована для вычис­ления предельной погрешности. Пусть заданы предельные значения погрешностей прямых измерений в виде 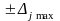и требуется оценить предельную погрешность ±_mах резуль­тата косвенного измерения. Тогда из (3.4.4) следует, что

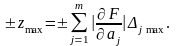(3.4.5)

Рассмотрим оценивание случайной погрешности резуль­татов косвенных измерений. Пусть величины измерены со случайными погрешностями _j, имеющими нулевые мате­матические ожидания М[ ]=0 и дисперсии 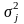. Исполь­зуя (3.4.4), запишем выражения для математического ожидания М[z] и дисперсии ²[z] погрешности z:

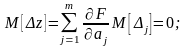(3.4.6)

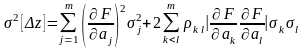, (3.4.7)

где 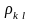– коэффициент корреляции погрешностей и

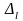
Если погрешности некоррелированы, то

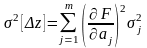. (3.4.8)

Таким образом, для оценки результата 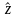косвенного измерения естественно применить формулу

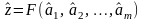, (3.4.9)

а для оценки систематических и случайных погрешностей соответственно (3.4.4) и (3.4.8).

В общем случае при нелинейной функции (3.4.1) коэффициенты влияния , присутствующие в этих формулах, в свою очередь являются функциями зна­чений величин . Коэффициенты влияния обычно оценива­ются путем подстановки в выражения частных производных оценок 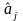. Следовательно, вместо самих коэффициен­тов влияния получают лишь их оценки. Кроме того, иногда коэффициенты влияния определяют экспериментально. В том и другом случае они устанавливаются с некоторой погрешностью, что является еще одним источником погреш­ности при обработке результатов косвенных измерений. Однако в некоторых частных, но распространенных на практике случаях указанная погрешность определения ко­эффициентов влияния отсутствует. Рассмотрим различные ситуации.

1. Функция 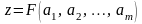линейна. Пусть

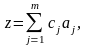(3.4.10)

где 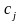– известные коэффициенты. Тогда коэффициенты влияния

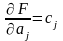, (3.4.11)

а формулы (3.4.4) и (3.4.8) приобретают следующий вид:

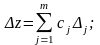(3.4.12)

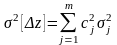. (3.4.13)

2. Функция логарифмируема. Пусть

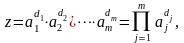(3.4.14)

где – известные числа, которые могут быть положительными или отрицательными, целыми или дробными.

Прологарифмируем, а затем продифференцируем (3.4.14):

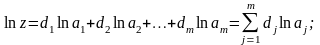(3.4.15)

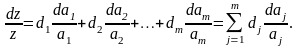(3.4.16)

Положив, что погрешности измерений малы, заменим в (3.4.16) дифференциалы соответствующими приращениями:

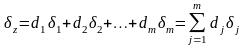, (3.4.17)

где 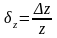; 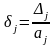– относительные погрешности.

Дисперсия случайной относительной погрешности

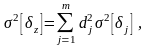(3.4.18)

где 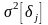– дисперсии случайных относительных погреш­ностей прямых измерений значений величин .

Как видно из полученных формул, в данном случае расчет погрешностей упрощается при переходе к оценкам относительных погрешностей измерений.

Пример 3.4.1. Дана функция 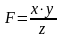, где x, y, z – некоррелированные аргументы, полученные измерениями со средними квадратиченскими отклонениями 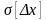, , 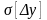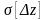. Определить .

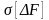Решение. Согласно (3.4.8) можем записать:

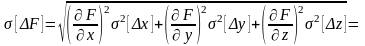
Пример 3.4.2. Мощность, поглощаемую в активном сопротив­лении, определяют косвенно путем измерения сопротивле­ния резистора и падения напряжения на нем с последую­щим вычислением по формуле 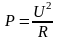. Предположим что получены следующие результаты: 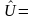10 В, 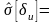0,5 %, 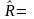100 Ом, 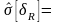1 %. Оценить относительную погрешность.

Решение. Преобразуем формулу:

.

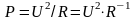Согласно (3.4.18)

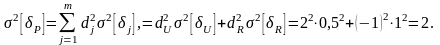
Тогда

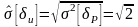
Вт, а  1,4%.

Пример 4.3.3. Найти значение электрической энергии и среднюю квадратическую погрешность ее определения по результатам измерения силы тока, сопротивления и времени, если I = (10,230 ± 0,015) А, R = (11,68 ± 0,01) Ом, t = (405,2 ± 0,1) с.

Решение. Для нахождения энергии воспользуемся формулой 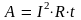. Согласно (3.4.18) формула относительной погрешности принимает вид:

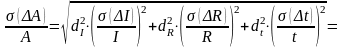
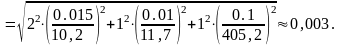
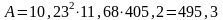кДж.

Пример 3.4.4. При измерении электрического сопротивления катушки приборами класса точности 1,0 получены следующие результаты: I = 17,2 мА, U = 440 мВ. Найти величину сопротивления и оценить точность измерения. Максимальное значение силы тока, измеряемое данным миллиамперметром, равно 75 мА, максимальное напряжение – 150 В.

Решение. Абсолютные предельные погрешности приборов составят:

I = 7510^-2 мА; U = 0,015 В.

Относительные погрешности равны:

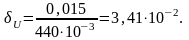
Значение сопротивления

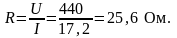
Относительная погрешность оценки сопротивления

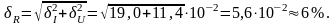
Абсолютная предельная погрешность оценки сопротивления

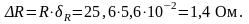
Таким образом, результат измерения должен быть записан в виде