5.7.1. Модели дискретизации аналогового сигнала

В основе математического описания дискретизации непрерывных функций лежат два теоретических положения: фильтрующее свойство -функции и теорема дискретизации.

Если сигнал дискретизируется с помощью переключателя, который периодически с интервалом Т замыкается на короткое время (рис. 5.7.2,а), на выходе такого дискретизатора образуется последовательность конечной длины. Для теоретических прило­жений удобно рассматривать идеальный дискретизатор, на выходе которого образуется последовательность импульсов (рис. 5.7.2,б), имеющих площадь 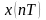, равную значению сигна­ла в моменты отсчетов t = 0, Т, …, nT. Этот процесс называют импульсной дискретизацией.

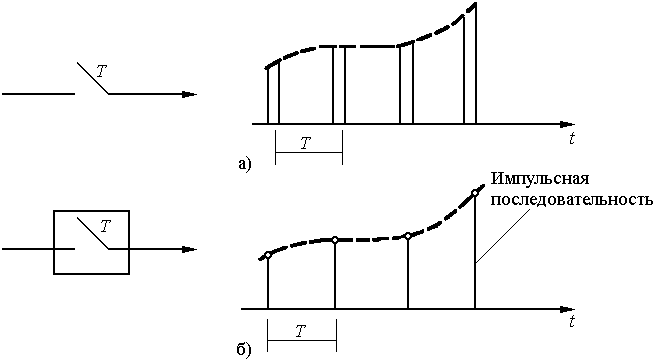
Рис. 5.7.2. Реальная (а) и идеальная (б) дискретизация

Идеальную дискретизацию можно сравнить с модуляцией с помощью несущей, когда «несущей» является непрерывная последовательность единичных импульсов, которую можно записать в виде последовательности -функций

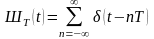. (5.7.1)

Такую последовательность называют гребенкой Дирака, а в технических приложениях – импульсной функцией дискрети­зации.

Пусть задан сигнал x(t), имеющий спектр X(). Осуществле­ние дискретизации x(t) с частотой F_S означает умножение функции x(t) на импульсную функцию дискретизации, исполня­ющую роль несущей, т.е.

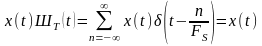, (5.7.2)

где – дискретизированный сигнал.

Если x(t) = 0, то модуляции нет, выходной сигнал отсутствует; если же x(t) – постоянная, то на выходе будет только несущая. Таким образом, импульсная дискретизация имеет те же свойства, что и модуляция с подавленной несущей, и выборки из сигнала x(t) являются весовыми коэффициен­тами -функции. Рассматривая -функцию как обобщен­ную функцию, найдем ее фурье-образ:

(5.7.3)

Отсюда получаем

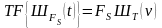. (5.7.4)

Как видно, фурье-образ гребенки Дирака есть также последовательность импульсов Дирака. Следовательно, дискре­тизацию можно проводить и по частоте.

Выясним структуру спектра дискретизированного сигнала . Представим (5.7.2) в виде

. (5.7.5)

Имея в виду формулу Пуассона

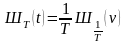, (5.7.6)

получим,

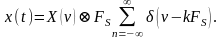(5.7.7)

Из (5.7.7) следует, что спектр дискретизированного сигнала представляет собой последовательность спектров Х(t) исходного сигнала x(t), сдвинутых один относительно другого на величину F_S.

Пусть фурье-образ для 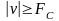, т.е. спектр сигнал; x(t) расположен на интервале (-F_C, F_C) длиной 2F_C. Тогда справедлива теорема дискретизации: для того чтобы периодическое повторение спектра, вызванное дискретизацией сигнала, не изменяло повторяемый спектр, необходимо и достаточно выполнение неравенства .

При решении практических задач дискретизации возникает ряд вопросов:

1) из каких соображений выбирать интервал дискретизации Т?

2) какова точность замены непрерывного сообщения дискретным?

3) каков максимально допустимый интервал дискретизации?

4) как передать по каналу связи дискретное сообщение и как его восстановить на приемном конце?

На все эти вопросы дает ответ более общая теорема дискретизации, сформулированная В.А. Котельниковым: если некоторая функция x(t) имеет спектр Фурье X(v), ограниченный полосой частот F_C, то эта функция может быть представлена с помощью дискретных отсчетов, взятых через интервалы времени, равные 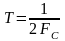; функция времени на интервале наблюдения Т_С может быт представлена с помощью п отсчетов, число которых .

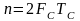На рис. 5.7.3 изображены функция времени x(t) и ее спектр 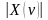с граничной частотой F_С.

Рис. 5.7.3. Функция времени (а) и спектр сигнала (б)

с ограниченной нелинейной частью

В соответствии с этой теоремой функция x(t) имеет следующее аналитическое разложение:

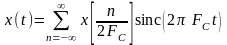, (5.7.8)

где 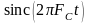– синк-функция или функция отсчетов

. (5.7.9)

Для дальнейшего анализа удобно ввести подвижную систему координат, т.е. сместим начало координат в точку отсчета обозначив . Тогда функция отсчетов примет вид

. (5.7.10)

В (5.7.8) величины 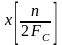представляют значения ис­ходной функции времени x(t), определяемые выражением (5.7.1); их называют отсчетами.

Функция отсчетов обладает следующими свойствами:

1) в момент отсчета она достигает своего наибольшего значения, равного единице;

2) в моменты времени , где p = 1, 2, 3 ..., функция обращается в нуль;

3) ширина главного лепестка функции отсчетов на нулевом уровне равна ;

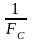4) функции отсчетов ортогональны на бесконечно большом интервале времени.

Функция отсчетов в виде (5.7.10) и ее спектр представлены на рис. 5.7.4.

Теорема, подтвержденная выражением (5.7.8), имеет ряд следствий:

1. Исходя из свойств функции отсчетов в разложении (5.7.8) в момент отсчета существует только одно слагаемое. Следовательно, чтобы передать по каналу связи сообщение, необходимо выполнить следующие операции: а) произвести отсчеты мгновенных значений передаваемого сообщения в моменты времени, отстающие один от другого на время интервал дискретизации; б) передать по каналу связи эти величины отсчетов любым из возможных методов; в) восстановить на приемном конце переданные отсчеты и сформировать импульсы, амплитуды которых были бы равны (или пропорциональны) переданным отсчетам, а длительности импульсов были бы малыми по сравнению с интервалами отсчетов; г) сформировать функции отсчетов, амплитуды которых были бы равны (или пропорциональны) переданным отсчетам; д) просуммировать полученные функции и получить, таким образом, функцию времени, пропорциональную (или равную) переданной функции времени.

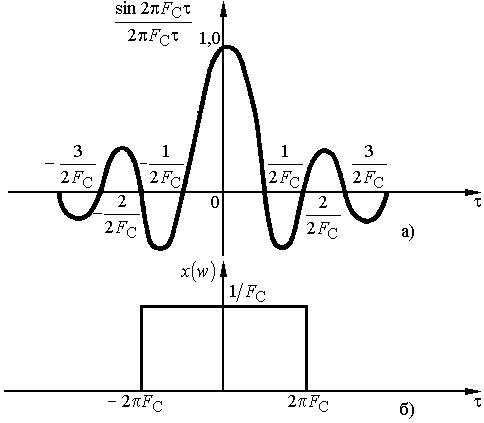
Рис. 5.7.4. Функция отсчетов (а) и ее спектр (б)

2. Разложение (5.7.8) можно интерпретировать как дискретный эквивалент свертки последовательности импульсов с амплитудой и с импульсной характеристикой синк-функции аналогового фильтра. Ясно, что эта импульсная характеристика идеального и, следовательно, физически нереализуемого фильтра нижних частот, имеющего передаточную функцию, равную постоянной величине Т в интервале 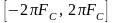и нулю вне его. Хотя этот фильтр физически нереализуем (его импульсная характеристика является опережающей), его можно все же аппроксимировать, использовав достаточно длительную временную задержку.

3. Разложение (5.7.8) определяет предельную дискретизацию. Действительно, если нарушаются условия первой и второй теорем дискретизации, то в системе возникает явление подмены частот – эффект наложения. Другими словами, если при измерениях с интервалом Т производится выбор значений синусоиды с частотой, большей 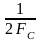, то такую выборку можно перепутать с выборкой синусоиды меньшей частоты. Значит, наряду с истинной частотой в выборке появляется и другая (меньшая) частота подмены. Например, в кинематографе колеса движущегося автомобиля всегда вращают в обратную сторону.