
- •200106 «Информационно-измерительная техника и технологии»
- •Введение
- •1.2. Сигналы
- •1.3. Преобразование измерительных сигналов
- •1.4. Спектр периодических сигналов
- •1.5. Модуляция
- •1.5.1. Амплитудная модуляция
- •1.5.2. Частотная модуляция
- •1.5.3. Фазовая модуляция
- •1.5.4. Двукратные виды модуляции
- •1.6. Квантование
- •1.6.1. Квантование по уровню
- •1.6.2. Квантование по времени
- •1.6.3. Квантование по уровню и времени
- •1.7. Кодирование
- •1.7.1. Цифровые коды
- •1.7.2. Помехи
- •1.8. Модель канала
- •Раздел 2 измерительные каналы и их разделение
- •2.1. Канал связи и его характеристики
- •2.2. Согласование канала с источником информации
- •2.3. Линии связи для передачи измерительной информации
- •2.4. Структуры линий связи
- •2.5. Многоканальные системы для передачи измерительной информации
- •2.6. Погрешность систем с частотным разделением каналов
- •2.7. Погрешности систем с временным разделением каналов
- •Раздел 3 принципы обработки данных
- •3.1. Виды погрешностей
- •3.2. Обработка результатов измерений. Оценки измеряемой величины
- •3.3. Обработка результатов прямых равноточных измерений
- •3.4. Обработка результатов косвенных измерений
- •3.5. Обработка результатов совместных измерений
- •3.6. Обработка результатов неравноточных измерений
- •3.7. Проверка статистических гипотез
- •3.7.1. Проверка соответствия гипотезы и экспериментальных данных
- •3.7.2. Исключение резко отклоняющихся значений
- •3.8. Построение эмпирических распределений
- •3.9. Критерии согласия
- •3.9.1. Критерий согласия Пирсона
- •3.9.2. Критерий согласия Колмогорова
- •Раздел 4 планирование многофакторного эксперимента
- •4.1. Задачи планирования эксперимента
- •4.2. Пассивные эксперименты
- •4.3. Дисперсионный анализ
- •4.4. Регрессионный анализ
- •4.5. Активный эксперимент
- •4.6. Полный факторный эксперимент
- •4.7. Дробный факторный эксперимент
- •4.8. Устранение влияния временного дрейфа
- •4.9. Проведение факторного эксперимента и обработка его результатов
- •4.10. Оптимизация
- •4.11. Рандомизация
- •Раздел 5 введение в алгоритмическую теорию измерений
- •5.1. Вводные замечания
- •5.2. Развитие понятий числа и измерения величин
- •5.3. Теория шкал и алгоритмические измерения
- •5.4. Алгоритмы измерения в номинальной шкале, аддитивной и порядка
- •5.5. Моделирование цифровых алгоритмических измерений
- •5.6. Эквивалентность между фильтрацией и алгоритмическим измерением
- •5.7. Моделирование сигналов. Дискретизация
- •5.7.1. Модели дискретизации аналогового сигнала
- •5.7.2. Дискретизация с усреднением
- •5.7.3. Дискретизация сигналов конечной длительности
- •5.8. Цифровое представление информации
- •5.9. Системы счисления с иррациональными основаниями
- •5.9.1. Золотая пропорция
- •5.9.2. Числа Фибоначчи
- •5.9.4. Код золотой p-пропорции
- •5.10. Общий алгоритм метрологического кодирования
- •5.10.1. Алгоритм Стахова
- •5.10.2.Фибоначчиевы алгоритмы цифрового метрологического кодирования
- •Раздел 6 введение в информационную теорию измерений
- •6.1. Основные положения теории информации
- •6.1.1. Энтропия
- •6.1.2. Единицы измерения энтропии
- •6.1.3. Условная энтропия (энтропия помехи)
- •6.1.4. Суммирование нескольких погрешностей
- •6.1.5. Явление «краевой эффект». Приближенность информационных оценок каналов передачи информации
- •6.1.6. Основные положения теории информации для характеристики процесса измерения
- •6.2. Сущность измерения
- •6.2.1. Понятие натурального ряда однородных величин
- •6.2.2. Понятие шкалы реперов измеряемой величины
- •6.2.3. Измерение как сужение интервала неопределенности
- •6.3. Измерительные преобразования, функциональные шкалы, единицы измеряемой величины
- •6.3.1. Функциональная шкала измеряемой величины
- •6.3.2. Понятие единицы измерения
- •6.3.3. Метод построения измерительных устройств
- •6.4. Измерительные преобразования и преобразователи
- •6.5. Энтропийное значение погрешности
- •6.5.1. Математическое определение энтропийного значения погрешности
- •6.5.2. Эффективное значение погрешности
- •6.6. Сравнение энтропийного и среднеквадратического значений погрешности для плавных симметричных одномодальных законов распределения погрешностей
- •6.7. Энтропийное значение погрешности – основной критерий точности приборов и измерений
- •6.8. Определение энтропийного значения погрешности на практике
- •6.9. Суммирование погрешностей измерительных устройств
- •6.10. Статистическое суммирование погрешностей при наличии корреляции
- •6.11. Энтропийное значение результирующей погрешности
- •6.12. Суммирование погрешностей с равномерными законами распределения вероятностей
- •6.13. Суммирование погрешностей при равномерном и нормальном законах распределения составляющих результирующей погрешности
- •6.14. Суммирование погрешностей при произвольной степени корреляции и произвольных законах распределения вероятностей составляющих результирующей погрешности
- •И объемов (n) выборок
- •Интервала
- •Оглавление
1.6. Квантование
При передаче измерительной информации по каналу связи она искажается под воздействием внутренних и внешних воздействий на сигнал. Дискретные сигналы в меньшей степени подвержены искажениям в процессе передачи, и эти искажения легче обнаружить. Информация, получаемая в дискретной форме, имеет ряд преимуществ по сравнению с аналоговой ее формой при хранении и обработке.
Операция замены аналоговой величины дискретной называется квантованием. При квантовании:
– вся область возможных значений разбивается на конечное число подобластей или интервалов квантования;
– каждому интервалу присваивается определенный индекс;
– попадание входного сигнала в любую точку интервала вызывает появление на выходе прибора индекса интервала.
1.6.1. Квантование по уровню
Процесс
квантования по уровню функции
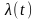 проиллюстрирован на рис. 1.6.1. В результате
квантования образуется ступенчатая
функция. Переход с одной ступени на
другую происходит в те моменты, когда
первоначально непрерывная функция
пересекает линию, проведенную посередине
интервала квантования.
проиллюстрирован на рис. 1.6.1. В результате
квантования образуется ступенчатая
функция. Переход с одной ступени на
другую происходит в те моменты, когда
первоначально непрерывная функция
пересекает линию, проведенную посередине
интервала квантования.
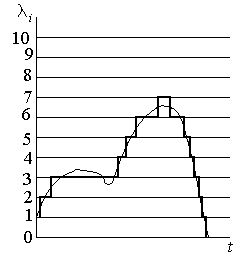
Рис. 1.6.1. Квантование сообщения по уровню функции
По оси ординат откладывается значение заранее выбранного шага квантования q и проводят линии, параллельные оси времени, обозначающие уровень квантования. При постоянном шаге квантования q имеется случай равномерного квантования.
Максимальная
ошибка квантования
 .
.
Погрешность квантования
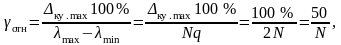 (1.6.1)
(1.6.1)
где
 – число интервалов;
– число интервалов;
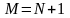 – число уровней квантования.
– число уровней квантования.
В
произвольный момент времени ошибка
квантования представляет собой
непрерывную случайную величину,
равномерно распределенную в интервале
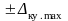 .
При условии, что
.
При условии, что
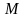 велико, все значения
в одном интервале квантования можно
считать равновероятными.
велико, все значения
в одном интервале квантования можно
считать равновероятными.
Например,
требуется найти число уровней квантования
и величину шага квантования q,
если
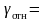 0,1%,
0,1%,
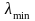 =150
В. Используя выражение для
=150
В. Используя выражение для
 ,
получим
,
получим
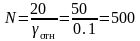 интервалов,
интервалов,
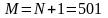 уровней. Для определения шага квантования
запишем
уровней. Для определения шага квантования
запишем
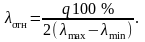 (1.6.2)
(1.6.2)
Так как
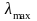 =0,
то
=0,
то
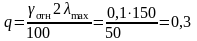 В.
В.
1.6.2. Квантование по времени
Замена
непрерывной функции ее отдельными
значениями в определенные моменты
времени называется квантование по
времени или дискретизацией. Процесс
дискретизации функции
показан на рис. 1.6.2. Горизонтальная ось
времени делится на интервалы, отстающие
друг от друга на интервал квантования
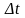 .
Далее проводятся вертикальные линии
до пересечения с квантуемой функцией,
а в точках 1, 2, 3, …, 13 определяются значения
функции, начиная с
.
Далее проводятся вертикальные линии
до пересечения с квантуемой функцией,
а в точках 1, 2, 3, …, 13 определяются значения
функции, начиная с
 .
.
Значения непрерывной функции будет передаваться не бесконечным рядом значения, а значениями функции в дискретные моменты времени. Очевидно, чем меньше шаг квантования, тем с большей точностью будет восстанавливаться на приеме функция , но при этом увеличивается число отсчетов функции.
Шаг
квантования определяют из теоремы
Котельникова, которая заключается в
том, что любая непрерывная функция,
спектр частот которой ограничен частотой
Fmax,
может быть полностью восстановлена по
ее дискретным значениям, взятым через
интервалы времени
 .
.

Рис. 1.6.2. Квантование сообщения по времени
Оптимальной является такая дискретизация, которая обеспечивает представление исходной функции с заданной точностью минимальным числом отсчетов. В этом случае все отсчеты существенны для восстановления исходной функции. В случае неоптимальной дискретизации, кроме существенных, производятся и избыточные отсчеты. Наличие избыточной информации:
– занимает канал связи на более длительное время;
– требует увеличивать объем памяти при хранении;
– увеличивает время поиска и считывания данных;
– уменьшает скорость обработки данных.
Поэтому дискретизацию по времени следует рассматривать не только как операцию преобразования непрерывного сообщения в дискретное, но и как один из методов устранения избыточной для потребителя информации.
