6.7. Энтропийное значение погрешности – основной критерий точности приборов и измерений

Любые методы определения или нормирования точности измерительных устройств или измерений сводятся к установлению значений характеризующих их погрешностей. Однако при экспериментальном определении эти значения выступают как частные реализации случайной величины, которая в полной мере может быть охарактеризована лишь законом распределения вероятностей, а более сжато – ее предельным, среднеквадратическим или энтропийным значением.

Если при этом признается бесспорным исходное положение о том, что основным результатом, ради получения которого используются измерительные устройства, является измерительная информация, то в качестве основного критерия качества этих устройств должен быть выбран критерий, однозначно связанный именно с количеством получаемой измерительной информации.

С точки зрения теории информации точность измерений однозначно определяется лишь значением энтропийной погрешности измерения, равной , где – энтропийный коэффициент, зависящий от вида закона распределения вероятностей погрешности, – среднеквадратическое значение погрешности, определяемое дисперсией, т.е. мощностью погрешности. При этом точность измерения с позиций теории информации не может быть определена лишь каким-то одним из этих двух показателей, а обусловлена их совокупностью.

В этих условиях возникает чрезвычайно важный как в практическом, так и в теоретическом плане вопрос о правомерности использования для оценки точности приборов или измерений максимального 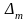, доверительного 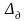или среднеквадратического значений погрешности. Действительно, если основной ценностью результата измерения является содержащаяся в нем информация о значении измеряемой величины, а критерии точности в виде , или не позволяют однозначно ее определить, то такие критерии должны быть признаны некорректными. Решением вопроса является использование такого критерия эффективного значения погрешности, который однозначно связан с информационным качеством результата измерения. Этим критерием служит энтропийное значение погрешности .

6.8. Определение энтропийного значения погрешности на практике

Энтропийное значение погрешности определяется выражением . Оно позволяет вычислить энтропийную погрешность по значению условной энтропии , т.е. энтропии закона распределения погрешности .

Однако при оценке точности измерительных устройств экспериментатор располагает не самим законом распределения погрешности , а лишь некоторым конечным числом n конкретных значений случайной величины , подчиняющихся этому закону. На основании этого ограниченного числа результатов может быть построена лишь ступенчатая гистограмма (рис. 6.8.1), в той или иной степени приближающаяся к действительному закону распределения . Поэтому практически желательно иметь формулу для вычисления энтропийного значения погрешности исходя из такой приближенной гистограммы.

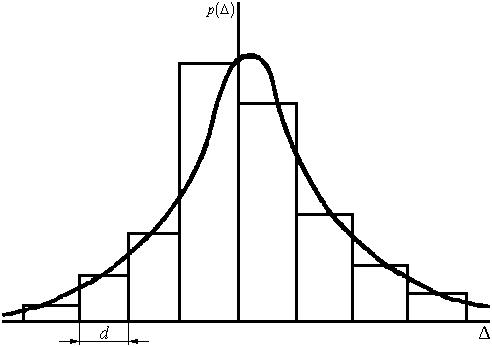
Рис. 6.8.1.Ступенчатая гистограмма

Если гистограмма состоит из т столбцов с границами 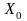, , , ..., , , ..., 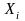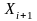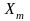и каждый столбец шириной 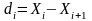включает в себя результатов, то плотность вероятности на протяжении каждого из столбцов остается постоянной и равной

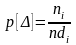. (6.8.1)

Энтропия такого ступенчатого распределения

(6.8.2)

Если ширина всех столбцов гистограммы одинакова, т.е. d_i = d, то

(6.8.3)

Таким образом, энтропия гистограммы определяется как взятая с обратным знаком сумма произведений вероятности случайной величины на логарифм этой вероятности, а член 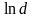обеспечивает независимость значения величины энтропии от произвольного выбора величины d ступеньки гистограммы.

Для расчетов это выражение можно представить как

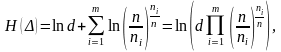(6.8.4)

тогда энтропийное значение погрешности будет равно

(6.8.5)

Исследование (6.8.5) показывает, что полученная оценка является смещенной, но это смещение убывает по мере увеличения n и m. При этом m и d могут выбираться произвольно, но с ограниче­нием , так как наличие интервалов или не изменяет энтропии, так как 1¹ = 1 и при определении энтропии полагают 0⁰ = 1.

Пользоваться (6.8.5) можно только тогда, когда общее число наблюдений п настолько велико, что может быть разбито на т (по крайней мере 57) интервалов шириной d_i, в крайние из которых еще попадает по 12 наблюдения. Это приводит к тому, что вычислить энтропийное значение погрешности исходя из основного определения можно лишь, располагая серией из 3050 наблюдений. Это и понятно, так как для определения энтропийного значения погрешности  требуется такой объем испытаний п, при котором уверенно определяется вид закона распределения вероятностей погрешностей, а следовательно, и его энтропия. Поэтому метод прямого вычисления энтропийного значения погрешности может быть использован только при обстоятельном исследовании характеризуемой погрешности, что связано с достаточно большой затратой времени.

Однако, используя связь между энтропийным и среднеквадратическим значениями погрешности через энтропийный коэффициент в виде , можно приближенно определить энтропийную погрешность. Идея заключается в том, что большая серия наблюдений необходима лишь для установления вида закона распределения, т.е. для определения величины энтропийного коэффициента , в то время как для установления ее дисперсии или среднеквадратического значения , достаточно относительно короткой серии, состоящей из 1530 наблюдений. Если надо вычислить энтропийное значение погрешности для ряда однотипных измерений, то обстоятельное исследование (50200 наблюдений) может быть проведено один раз с целью установления значения энтропийного коэффициента . Предполагая, что значение остается неизменным, все последующие испытания могут состоять из серий по 1530 наблюдений, проводимых только для определения среднеквадратического значения погрешности, а энтропийное значение погрешности может вычисляться как .

Более простой метод определения энтропийной погрешности состоит в предварительной классификации измерений по значениям присущего им энтропийного коэффициента. Например, даже из небольшой статистики исследования можно выделить определенные группы измерений с характерными для них значениями энтропийного коэффициента. Конечно, малая статистика не достаточна для присвоения тем или иным группам измерений определенных значений энтропийного коэффициента. Для этого подобная работа должна быть проделана в более крупном масштабе с целью получения более представительной статистики. Однако сам метод нахождения энтропийной погрешности реальных измерений по заранее выбираемому значению энтропийного коэффициента (из ряда 1,6; 1,7; 1,8) и по , получаемой из небольшой серии испытаний, по-видимому, целесообразен.

Можно также использовать упрощенный метод определения энтропийного значения погрешности  как 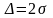, где в качестве предельного округленного значения энтропийного коэффициента для любых измерений принимается значение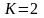 .