6.1.6. Основные положения теории информации для харак­теристики процесса измерения

Точность измерений обычно характеризуется числовым значением полученных при измерении или предполагаемых погрешностей. При этом используются понятия абсолютной и относительной приведенной погрешностей. Если измерительное устройство имеет диапазон измерения от Х₁ до Х₂, т.е. может измерять величины, находящиеся в пределах от Х₁ до Х₂ с абсолютной погрешностью ±, не зависящей от текущего значения х измеряемой вели­чины, то, полученный результат измерения в виде показания Х_П записы­вается как Х_П ±  и характеризуется относительной приведенной погрешностью .

Рассмотрение этих же самых действий с позиций теории информации носит несколько иной характер, отличающийся тем, что всем перечисленным понятиям придается вероятностный, статистический смысл, а итог проведенного измерения истолковывается как сокращение области неопределенности измеряемой величины. В теории информации тот факт, что измерительный прибор имеет диапазон измерений от Х₁ до Х₂, означает, что при использовании этого прибора могут быть получены показания Х_П только в пределах от Х₁ до Х₂. Другими словами, вероятность получения отсчетов, меньших Х₁ и больших Х₂ равна нулю. Вероятность же получения отсчета где-то в пределах от Х₁ до Х₂ равна единице.

Если предположить, что плотность вероятности распределения различных значений измеряемой величины вдоль всей шкалы прибора одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком распределения плотности вероятности р(х) вдоль шкалы значений х, показанным на рис. 6.1.1.

Так как полная вероятность получить отсчет где-то в пределах от Х₁ до Х₂ равна единице, то под кривой р(х) должна быть заключена площадь, равная единице. При равномерном распределении плотности вероятности это приводит к .

После проведения измерения получаем показание прибора, равное Х_П. Однако вследствие погрешности прибора, равной ±, утверждать, что измеряемая величина точно равна значению Х_П нельзя. Поэтому результат измерения записываем в виде Х_П ± . Это озна­чает, что действительное значение измеряемой величины X лежит где-то в пределах от Х_П +  до Х_П – , т.е. в пределах участка 2, как показано на рис. 6.1.1.

Рис. 6.1.1. График распределения плотности вероятности р(х)

С точки зрения теории информации результат измерения состоит лишь в том, что до измерения область неопределенности про­стиралась от Х₁ до Х₂ и характеризовалась малой плотностью вероятности , а после измерения она сократилась до величины 2 и характеризуется намного большей плотностью вероятности 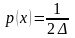. Получение какой-либо информации об интересующей величине заключается, таким образом, в уменьшении неопределенности ее значения.

Формальный прием для математической записи этого логического заключения достаточно состоит в определении количества информации q как уменьшения энтропии от значения , которое характеризует неопределенность измеряемой величины перед измерением, до значения , которое остается после получения показания прибора , т.е. как

(6.1.10)

Величина представляет собой исходную энтропию, а значение характеризует ту неопределенность, которая остается после получения показания прибора и называется условной энтропией (при условии, что известно).

В приведенном примере с равномерным законом распределения плотности вероятности как до, так и после измерения исходная, или безусловная, энтропия составляет

(6.1.11)

а оставшаяся, или условная, энтропия результата измерения получения отсчета равна

. (6.1.12)

Отсюда полученное количество информации, равное разности исходной и оставшейся энтропии, записывается как

(6.1.13)

В этой замене операции деления  на , используемой обычно при определении относительной погрешности измерения, на операцию вычитания исходной и оставшейся неопределенностей, характеризуемых соответствующими значениями энтропии, и заключается основной прием анализа теории информации.