1.5.2. Частотная модуляция
При частотной модуляции частота синусоидального сигнала (переносчика) изменяется по закону изменения передаваемого сигнала. При этом его амплитуда не меняется. Выражение для частотно-модулированного сигнала имеет вид
(1.5.10)
где
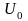– амплитуда;
– частота несущего колебания;
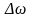– максимальное отклонение частоты от
(это отклонение пропорционально амплитуде
модулированного сигнала).
Подставив
в это выражение значение
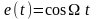(модулирующий сигнал, несущий информацию),
получим
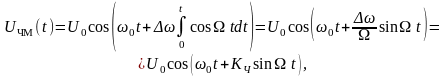(1.5.11)
где
– коэффициент частотного отклонения
или индекс частотной модуляции.
Частотно-модулированный
сигнал состоит из несущей частоты с
амплитудой
и двух бесконечных боковых полос
и
,
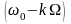внутри которых частоты отстоят друг от
друга на величину .
Спектр частотно-модулированного сигнала
бесконечно велик. Полоса частот при
частотной модуляции находится как
.
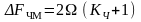Оптимальная величина
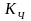зависит от требуемой точности передачи.
Так для информационно-измерительных
систем при выполнении измерений с
погрешностью = 1%
= 5,
а при = 0,1%
= 15.
Частотная модуляция имеет ряд преимуществ перед амплитудной модуляцией. Хотя техническая реализация частотной модуляции сложнее амплитудной и занимаемая полоса частот частотной модуляцией значительно выше, чем при амплитудной модуляции, но помехоустойчивость частотной модуляции значительно выше, при амплитудной. Это связано с тем, что помехи воздействуют в первую очередь на амплитуду сигнала, что при частотной модуляции существенного значения не имеет. Из-за плохой помехоустойчивости амплитудной модуляции она как самостоятельный вид модуляции применяется редко, а используется обычно как промежуточный вид модуляции при двойных модуляциях типа АМ – ЧМ и ЧМ – АМ.
1.5.3. Фазовая модуляция
При фазовой модуляции передаваемое сообщение изменяет значение фазы переносчика. Таким образом, фаза несущей частоты изменяется прямо пропорционально мгновенным значениям тока или напряжения модулирующего сигнала. Выражение для фазовой модуляции имеет вид:
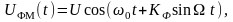(1.5.12)
где
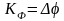– максимальный сдвиг по фазе или девиация
фазы.
Полоса частот, занимаемая таким сигналом, будет равна
(1.5.13)
При
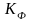>>1
спектр частот при фазовой модуляции
похож на спектр частот частотной
модуляции. При
<<1
спектр частот
.
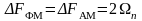Фазовая модуляция аналогична частотной,
и отличаются они друг от друга лишь
методами их осуществления.
1.5.4. Двукратные виды модуляции
Они обладают рядом достоинств, в том числе позволяют повысить помехоустойчивость передачи сообщения. При модуляции типа АМ – ЧМ сначала сообщением модулируется по амплитуде первый переносчик, который называется поднесущей. Далее амплитудно-модулированный сигнал модулирует второй переносчик, или несущую частоту. В результате этого имеем сигнал, модулированный по частоте (рис. 1.5.5).
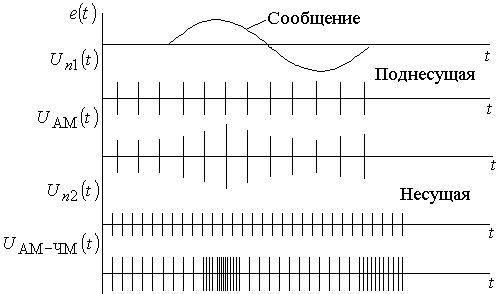
Рис. 1.5.5. Двукратная модуляция типа АМ – ЧМ
Иногда применяется модуляция ЧМ – АМ, при которой помехоустойчивость обеспечивается ЧМ, а экономия полосы частот – АМ. При этом поднесущая частота модулируется по частоте, а затем частотно-модулированный сигнал модулирует несущую частоту по амплитуде. По такому же принципу осуществляется модуляция ЧМ – ЧМ.
Используя серию импульсов в качестве переносчика, можно под воздействием сообщения в зависимости от изменяемых параметров переносчика (амплитуда импульсов, длительность импульсов, число импульсов и т.д.) получить импульсную модуляцию. Так как параметров у такого переносчика много, то и число импульсных методов модуляции достаточно велико: амплитудно-импульсная (АИМ), широтно-импульсная (ШИМ), времяимпульсная (ВИМ), частотно-импульсная (ЧИМ), кодоимпульсная (КИМ) модуляции и др. Для импульсных методов модуляции характерна зависимость ширины полосы частот модулированного сигнала от длительности импульса переносчика.