Раздел 6 введение в информационную теорию измерений
6.1. Основные положения теории информации
Основные положения теории информации были разработаны К. Шенноном в его работах 1948, 1949 и 1950 гг. «Основная идея теории информации состоит в том, что с информацией можно обращаться почти так же, как с такими физическими величинами, как масса или энергия» – писал К. Шеннон. Поэтому система транспортировки информации может рассматриваться подобно системам транспортировки массы или энергии.
В первой из этих работ Шеннон формулирует основные соотношения теории информации в виде 23 теорем. Во второй работе приводится пять теорем, которые в основном соответствуют теоремам 13, 17, 18, 11 и 23 первой работы. По тематике эти 23 теоремы Шеннона можно подразделить на три группы. Первая группа (теоремы 2, 10, 11, 13, 15, 16, 17) обосновывает систему общих оценок процесса передачи информации. Вторая (теоремы 18 23) – это ряд попыток получения приближенных оценок для некоторых частных случаев. И, наконец, наибольшую группу составляют 10 теорем (1, 3, 4, 5, 6, 7, 8, 9, 12 и 14), посвященных вопросам оптимального кодирования передаваемой информации.
В этой связи разработанную Шенноном теорию часто называют не «теорией информации», а «шенноновской теорией оптимального кодирования информации». Однако взгляд на теорию информации как на «теорию оптимального кодирования» весьма ее обедняет, так как теория совокупных информационных оценок систем приема и передачи информации и, в частности, измерительных систем является столь же важным разделом теории информации, как и теория кодирования.
6.1.1. Энтропия
В теории вероятностей в качестве критериев, описывающих законы распределения, используются начальные моменты: математическое ожидание (первый начальный момент), начальный момент s-порядка; центральные моменты: центральный момент s-порядка, дисперсия (второй центральный момент), коэффициент асимметрии (третий центральный момент). Для теории информации К. Шеннон предложил свою систему критериев, кратко описывающих законы распределения. Для характеристики систематической составляющей используется, как и прежде, первый начальный момент, т.е. значение математического ожидания, а для характеристики центрированной случайной составляющей вместо всех моментов более высоких порядков используется своеобразный момент, равный для закона распределения р(х) интегралу
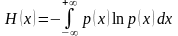(6.1.1)
и называемый энтропией. Таким образом, энтропия является функционалом закона распределения случайной величины и учитывает особенности этого закона. Вывод этого соотношения К. Шеннон сформулировал в виде теоремы 2. Смысл этой теоремы можно пояснить следующим образом.
Пусть некоторый ряд значений случайной величины X имеет нормированные вероятности Р1, Р2, ..., Рn, т.е. известен закон распределения этих значений. Можно ли найти меру того, насколько неопределенна эта величина? Если имеется такая мера H (Р1, Р2, ..., Рn,), то Шеннон утверждает, что разумно потребовать, чтобы она обладала следующими свойствами:
1. Величина H должна быть непрерывной относительно Pi.
2. Если все п
значений Pi
равны между
собой, т.е.
,
то H
должна монотонно возрастать по мере
увеличения числа п,
так как
неопределенность при этом, естественно,
увеличивается.
3. Если выбор данного значения х может быть сделан путем двух или более последовательных выборов, то величина H не должна зависеть от этой последовательности, т.е. общая H должна быть взвешенной суммой индивидуальных значений H.
Теорема 2. Существует единственная функция H, удовлетворяющая перечисленным свойствам. Эта функция имеет вид
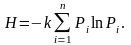(6.1.2)
Энтропию непрерывного распределения р(х) Шеннон определяет как
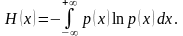
На основании этого
соотношения энтропия, например,
равномерного распределения, когда
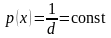в полосе шириной
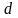и равно нулю
вне этой полосы, составляет
(6.1.3)
Энтропия дискретной случайной величины не зависит от того, какие именно значения принимает эта величина (важны количество этих значений и их вероятности), и равна
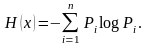(6.1.4)
Если рассмотреть случайную дискретную величину X, которая имеет n равновероятных значений, то вероятность каждого из них будет равна и
(6.1.5)
т.е. энтропия системы с равновероятными состояниями равна логарифму количества этих состояний. Чем больше число возможных состояний системы при равновероятности их появления, тем больше неопределенность системы или возможность выбора. Иначе можно сказать, что энтропия есть мера свободы выбора.