5.10.2.Фибоначчиевы алгоритмы цифрового метрологического кодирования

Обозначим через F_p(n) – функцию, разбивающую отрезок АВ на n равных интерва­лов единичной длины, т.е. AB = F_p(n). Следует заметить, что алгоритмы функционирования и структурные схемы АЦП в кодах Фибо­наччи и золотой пропорции ничем принципиально не отлича­ются от алгоритмов и структурных схем АЦП в классическом двоичном коде. Рассматриваемые ниже алгоритмы относятся к числу алгоритмов поразрядного кодирования. Однако положенные в основу этих алгоритмов ЦМК соотношения, связывающие веса двоичных разрядов, придают АЦП в кодах Фибоначчи и золотой пропорции ряд новых качественных свойств.

В алгоритме используются две дискретные переменных п и р, которые определяют значение шага алгоритма. Но переменная р является параметром используемого р-кода Фибоначчи и одновременно выполняет функции оператора сдвига дискретной временной оси. В зависимости от соот­ношения между п и р можно выделить два случая.

1. п  р + 1. В этом случае после первого шага кодирования в распоряжении алгоритма остается п-1 шагов, а так как р  п - 1, то кодирование фактически заканчивается после первого шага. Рекуррентная формула для вычисления функции F_p(n) имеет вид

(5.10.7)

Введем следующее определение:

(5.10.8)

Раскладывая в (5.10.7) по той же рекуррентной формуле п раз, с учетом (5.10.8) получаем

(5.10.9)

Переходя к системе мер, заметим, что оптимальная система мер в этом случае состоит из п единичных мер {1, 1, 1, ..., 1}, а оптимальный n-шаговый алгоритм кодирования заключается в том, что на каждом шаге кодирования очередная единичная мера прибавляется до тех пор, пока сравниваемая величина больше суммы мер. И этот процесс продолжается либо до исчерпания всех мер, либо до получения нулевого результата сравнения. Указанный алгоритм кодирования, как уже упомина­лось, широко распространен в технике аналого-цифрового преобразования под названием алгоритма последовательного счета.

2. п > р + 1. В этом случае рекуррентная формула для вычисления функции F_p(n) имеет вид

(5.10.10)

Объединяя (5.10.7), (5.10.9) и (5.10.10), получаем следующую рекуррентную формулу для вычисления функции F_p(n) в общем случае:

(5.10.11)

Для перехода к системе шкал с соответствующими мерами введем обозначения: – мера старшей шкалы; – мера младшей шкалы. Тогда при п > р + 1 система мер для реализации оптимального n-шагового алгоритма кодирова­ния будет определяться последовательностью , причем первые (р + 1) мер имеют единич­ный вес, т.е.

, (5.10.12)

а каждая последующая мера , где l > р, вычисляется по рекуррентной формуле

. (5.10.13)

Можно показать, что между функцией F_p(n) задаваемой выражением (5.10.11), и функцией задаваемой выражениями (7.10.12), (7.10.13), существует следующая связь:

. (5.10.14)

Другими словами, функция F_p(n) есть сдвиг последователь­ности вправо на р цифр р-ряда Фибоначчи.

Таким образом, при заданном р  0 оптимальный n-шаговый алгоритм ЦМК с помощью системы мер осуществляет разбиение отрезка АВ на равных интервалов единичной длины. Можно показать, что при заданном р оптимальная система мер задается с помощью р-чисел Фибоначчи. Поэтому описанные выше алгоритмы ЦМК называют фибоначчиевыми алгоритмами.

Рассмотрим частные случаи этих алгоритмов. Пусть р = 0. В этом случае система мер является двоичной, а фибоначчиевый алгоритм совпадает с алгоритмом поразрядного кодирования.

Пусть р = . В этом случае система мер состоит из единичных мер {1, 1, ..., 1}, а фибоначчиевый алгоритм совпа­дает с алгоритмом последовательного счета.

Пример 5.10.1. Зададимся р = 1 и рассмотрим поведение n-шагового фибоначчиевого алгоритма на отрезке АВ. Для этого вычислим значения функций F₁(n) и по рекуррентным формулам (5.10.11)  (5.10.14):

N	0	1	2	3	4	5	6	7	8
F1(n)	1	2	3	5	8	13	21	34	55
	1	1	2	3	5	8	13	21	34

Оптимальный n-шаговый алгоритм кодирования разбивает отрезок АВ на F₁(n) частей; это осуществляется с помощью системы мер , , 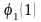..., . Пусть необходимо закодировать 5 разрядов. В этом случае 5-шаговый алгоритм кодирования разбивает отрезок АВ на F₁(5) = 13 частей, при этом используется система из 5 мер: 1, 1, 2, 3, 5. Рассмотрим первые два шага указанного 5-шагового алгоритма кодирования, действующего на отрезке [0, 13].

Первый шаг. Компаратор прикладывается к точке 5 и разбивает отрезок [0, 13] в «фибоначчиевом» отношении 5 + 8 (рис. 5.10.1,а).

Второй шаг. Если компаратор показал «вправо» (код 1), то интервал неопределенности сужается до отрезка [5, 13] в «фибоначчиевом» отношении 3 + 5 (рис. 5.10.1,б).

Если компаратор показал «влево» (код 0), то интервал неопределенности сужается до отрезка [0, 5] (рис. 5.10.1,в) и на втором шаге запрещается прикладывать компаратор к точкам отрезка [0, 5]. В этом случае при приложении компаратора к точке 2 отрезок [0, 5] разбивается в «фибоначчие­вом» отношении 2 + 3 (рис. 5.10.1,в).

Рис. 5.10.1. Пример фибоначчиевого алгоритма кодирования

Последующие шаги "фибоначчиевого" алгоритма аналогичны первым двум шагам и состоят в разбиении интервалов неопределенности каждый раз в "фибоначчиевом" отношении.