
- •200106 «Информационно-измерительная техника и технологии»
- •Введение
- •1.2. Сигналы
- •1.3. Преобразование измерительных сигналов
- •1.4. Спектр периодических сигналов
- •1.5. Модуляция
- •1.5.1. Амплитудная модуляция
- •1.5.2. Частотная модуляция
- •1.5.3. Фазовая модуляция
- •1.5.4. Двукратные виды модуляции
- •1.6. Квантование
- •1.6.1. Квантование по уровню
- •1.6.2. Квантование по времени
- •1.6.3. Квантование по уровню и времени
- •1.7. Кодирование
- •1.7.1. Цифровые коды
- •1.7.2. Помехи
- •1.8. Модель канала
- •Раздел 2 измерительные каналы и их разделение
- •2.1. Канал связи и его характеристики
- •2.2. Согласование канала с источником информации
- •2.3. Линии связи для передачи измерительной информации
- •2.4. Структуры линий связи
- •2.5. Многоканальные системы для передачи измерительной информации
- •2.6. Погрешность систем с частотным разделением каналов
- •2.7. Погрешности систем с временным разделением каналов
- •Раздел 3 принципы обработки данных
- •3.1. Виды погрешностей
- •3.2. Обработка результатов измерений. Оценки измеряемой величины
- •3.3. Обработка результатов прямых равноточных измерений
- •3.4. Обработка результатов косвенных измерений
- •3.5. Обработка результатов совместных измерений
- •3.6. Обработка результатов неравноточных измерений
- •3.7. Проверка статистических гипотез
- •3.7.1. Проверка соответствия гипотезы и экспериментальных данных
- •3.7.2. Исключение резко отклоняющихся значений
- •3.8. Построение эмпирических распределений
- •3.9. Критерии согласия
- •3.9.1. Критерий согласия Пирсона
- •3.9.2. Критерий согласия Колмогорова
- •Раздел 4 планирование многофакторного эксперимента
- •4.1. Задачи планирования эксперимента
- •4.2. Пассивные эксперименты
- •4.3. Дисперсионный анализ
- •4.4. Регрессионный анализ
- •4.5. Активный эксперимент
- •4.6. Полный факторный эксперимент
- •4.7. Дробный факторный эксперимент
- •4.8. Устранение влияния временного дрейфа
- •4.9. Проведение факторного эксперимента и обработка его результатов
- •4.10. Оптимизация
- •4.11. Рандомизация
- •Раздел 5 введение в алгоритмическую теорию измерений
- •5.1. Вводные замечания
- •5.2. Развитие понятий числа и измерения величин
- •5.3. Теория шкал и алгоритмические измерения
- •5.4. Алгоритмы измерения в номинальной шкале, аддитивной и порядка
- •5.5. Моделирование цифровых алгоритмических измерений
- •5.6. Эквивалентность между фильтрацией и алгоритмическим измерением
- •5.7. Моделирование сигналов. Дискретизация
- •5.7.1. Модели дискретизации аналогового сигнала
- •5.7.2. Дискретизация с усреднением
- •5.7.3. Дискретизация сигналов конечной длительности
- •5.8. Цифровое представление информации
- •5.9. Системы счисления с иррациональными основаниями
- •5.9.1. Золотая пропорция
- •5.9.2. Числа Фибоначчи
- •5.9.4. Код золотой p-пропорции
- •5.10. Общий алгоритм метрологического кодирования
- •5.10.1. Алгоритм Стахова
- •5.10.2.Фибоначчиевы алгоритмы цифрового метрологического кодирования
- •Раздел 6 введение в информационную теорию измерений
- •6.1. Основные положения теории информации
- •6.1.1. Энтропия
- •6.1.2. Единицы измерения энтропии
- •6.1.3. Условная энтропия (энтропия помехи)
- •6.1.4. Суммирование нескольких погрешностей
- •6.1.5. Явление «краевой эффект». Приближенность информационных оценок каналов передачи информации
- •6.1.6. Основные положения теории информации для характеристики процесса измерения
- •6.2. Сущность измерения
- •6.2.1. Понятие натурального ряда однородных величин
- •6.2.2. Понятие шкалы реперов измеряемой величины
- •6.2.3. Измерение как сужение интервала неопределенности
- •6.3. Измерительные преобразования, функциональные шкалы, единицы измеряемой величины
- •6.3.1. Функциональная шкала измеряемой величины
- •6.3.2. Понятие единицы измерения
- •6.3.3. Метод построения измерительных устройств
- •6.4. Измерительные преобразования и преобразователи
- •6.5. Энтропийное значение погрешности
- •6.5.1. Математическое определение энтропийного значения погрешности
- •6.5.2. Эффективное значение погрешности
- •6.6. Сравнение энтропийного и среднеквадратического значений погрешности для плавных симметричных одномодальных законов распределения погрешностей
- •6.7. Энтропийное значение погрешности – основной критерий точности приборов и измерений
- •6.8. Определение энтропийного значения погрешности на практике
- •6.9. Суммирование погрешностей измерительных устройств
- •6.10. Статистическое суммирование погрешностей при наличии корреляции
- •6.11. Энтропийное значение результирующей погрешности
- •6.12. Суммирование погрешностей с равномерными законами распределения вероятностей
- •6.13. Суммирование погрешностей при равномерном и нормальном законах распределения составляющих результирующей погрешности
- •6.14. Суммирование погрешностей при произвольной степени корреляции и произвольных законах распределения вероятностей составляющих результирующей погрешности
- •И объемов (n) выборок
- •Интервала
- •Оглавление
5.4. Алгоритмы измерения в номинальной шкале, аддитивной и порядка
Рассмотрим алгоритмы измерения в номинальной, порядка и аддитивной шкалах, которые широко используют в измерительной практике.
Измерение в номинальной шкале является самым примитивным. Его реализация требует воспроизведения измерительной шкалы с помощью по крайней мере п-1 мер, где п – численность семейства, к которому принадлежит исследуемое свойство. Измерение можно реализовать методом одновременных или последовательных сравнений. В последнем случае шкала формируется неупорядоченным образом. Алгоритм измерения в номинальной шкале представлен на рис. 5.4.1,а. Индекс i упорядочивает меры чисто формально.

Рис. 5.4.1. Алгоритмы измерения в номинальной (а), булевой (б)
и порядковой (в) шкалах
Примером измерения в номинальной шкале может служить измерение в булевой шкале, которая воспроизводится единственной мерой ul с булевым значением 0 или 1. Измерение состоит всего из одного сравнения. Алгоритм измерения в булевой шкале представлен на рис. 5.4.1,б.
Порядковая непрерывная шкала может быть воспроизведена с помощью конечного числа мер иi со свойствами vi, представляющими числа хi. Результат измерения по непрерывной порядковой шкале имеет интервальную форму, и его можно реализовать методом одновременных сравнений либо методом поочередных сравнений, формируя развертывающуюся или шаговую шкалу.
Развертывание заключается в формировании последовательности мер {ui} = {ul, u2, ..., uj ...} со свойствами, упорядоченными в соответствии с отношением порядка шкалы. Индекс i одновременно задает последовательность сравнения. Алгоритм измерения в порядковой развертывающейся шкале показан на рис. 5.4.1,в.
При формировании с накоплением последовательность мер, участвующих в сравнении, имеет вид {ui} = {ui1, ui2, ..., uij, ...}, где индекс i упорядочен в соответствии с порядком шкалы, а индекс j указывает очередность сравнения. Значение мер в j-м сравнении зависит от результата предыдущих j-1 сравнений с мерами ujα, α = l, 2, ..., j-1.
Принцип шагового
формирования порядковой шкалы можно
теперь записать в виде

Алгоритм измерения в порядковой шкале с шаговым формированием приведен на рис. 5.4.2.
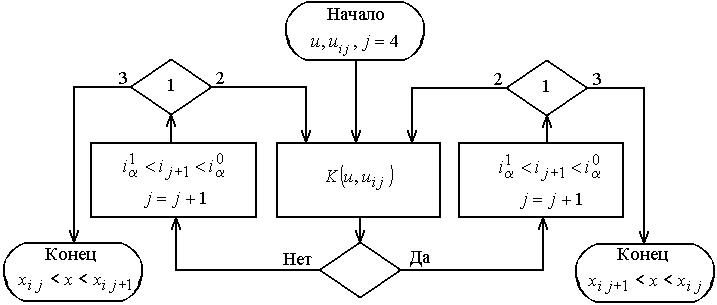
Рис. 5.4.2. Алгоритм измерения в порядковой шкале с шаговым
формированием:
1 – неравенство; 2 – выполнено; 3 – не выполнено
Измерение в
аддитивной непрерывной шкале является
иерархически самым высоким. Аддитивную
шкалу можно воспроизвести из первичных
мер, при умножении и суммировании их
значений можно сформировать произвольное
значение шкалы
 ,
где
,
где
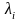 – кратность
мер (действительные числа);
– кратность
мер (действительные числа);
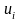 – численные
значения эталонов.
– численные
значения эталонов.
Измеряемая
аналоговая величина х
перед
сравнением с w
подвергается в общем случае нормализации,
состоящей в ее умножении на число и
прибавлении эталонных значений на
выходе устройства нормализации
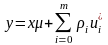 ,
где µ – коэффициент деления измеряемой
величины;
– кратность
мер;
,
где µ – коэффициент деления измеряемой
величины;
– кратность
мер;
 – значения
эталонов.
– значения
эталонов.
Сравниваемые
величины w
и у
по
своей природе непрерывны, однако в
зависимости от способа их формирования
они могут быть либо непрерывными (т.е.
принимать любые численные значения),
либо ступенчатыми (т.е. принимать только
некоторые значения). Ступенчатое
формирование имеет место в том случае,
когда кратности мер
 могут принимать только целые значения.
могут принимать только целые значения.
Результат измерения
в непрерывной аддитивной шкале имеет
интервальную форму
 где х –
истинное значение измеряемой величины;
где х –
истинное значение измеряемой величины;
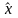 – оценка значения измеряемой величины;
– оценка значения измеряемой величины;
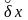 ,
,
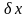 – предельные
погрешности измерения.
– предельные
погрешности измерения.
Алгоритм измерений в аддитивной развертывающейся шкале представлен на рис. 5.4.3,а.
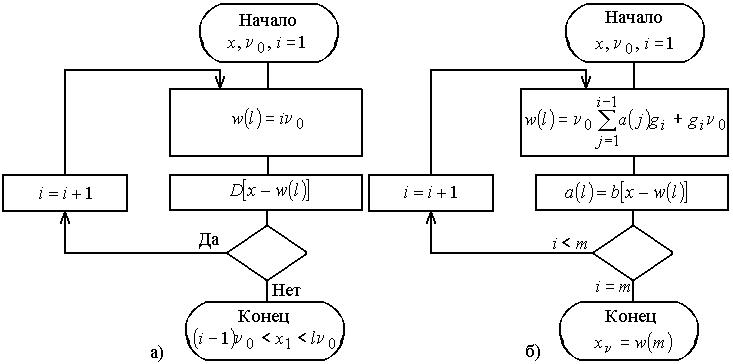
Рис. 5.4.3. Алгоритмы измерения в аддитивной шкале (а) и аддитивной шкале с шаговым формированием (б)
Шаговое формирование
заключается обычно в суммировании
эталонных значений
,
кратных кванту
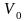 :
:
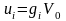 ,
где
,
где
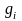 – целые числа,
именуемые весами, такие, что из интервала
(0, М) каждое
целое число
– целые числа,
именуемые весами, такие, что из интервала
(0, М) каждое
целое число
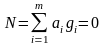 или 1.
или 1.
В последовательных тактах формируются эталонные значения:
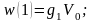

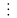

Измерение заканчивается в (m+1)-м такте, в котором
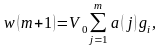
где
значение
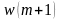 удовлетворяет
условию
удовлетворяет
условию
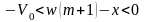 .
Алгоритм измерения в аддитивной шкале
с шаговым формирователем показан на
рис. 5.4.3,б.
.
Алгоритм измерения в аддитивной шкале
с шаговым формирователем показан на
рис. 5.4.3,б.
