
- •Формула называется формулой с тесными отрицаниями, если в ней нет связок þ и û, и отрицания относятся только к пропозициональным переменным.
- •§ Кванторы
- •§ Элементы теории множеств
- •§ Операции над множествами
- •§ Операции соответствия между множествами
- •Физические типы соответствий:
- •Def: Множества, равномощные множеству точек, принадлежащих интервалу (0, 1) называются множествами мощности континиум. Пример: Множество вещественных чисел r является множеством мощности континиум.
- •Раздел 2. Предел и непрерывность § грани числовых множеств
- •§ Расположение точек относительно множества
- •§ Предел функции по коши Рассматриваются числовые функции числового аргумента:
- •Запишем еще раз определение предела функции на языке e-d:
- •Внимательно рассмотрев определение предела нетрудно установить, что:
- •Запишем теперь сокращенное определение того, что f (X) ® b при X ® а на языке e-d:
- •Словарик
- •§ Непрерывность функции
- •§ Непрерывность элементарных функций
- •Примеры элементарных функций:
- •§ Предел последовательности
- •Примеры:
- •Раздел 3. Бесконечно малые и др. Величины § определения, терминология и примеры
- •Раздел 4. Непрерывные функции
- •§ Частичные пределы
- •§ Предельный переход в равенствах и неравенствах
- •§ Непрерывность тригонометрических функций
- •Раздел 5. Замечательные пределы § Первый замечательный предел
- •§ Арифметические действия над монотонными функциями.
- •§ Бином Ньютона
- •§ Предел функции по гейне ( по последовательности)
- •§ Второй замечательный предел
- •§ НепрЕрывность показательной функции
- •§ НепрЕрывность логарифмической функции
- •§ Пределы, связанные с показательными, логарифмическими и степенными функциями
- •§ Степенные асимптотические разложения
- •§ Действия над асимптотическими разложениями.
- •§ Асимптотические разложения Маклорена для основных элементарных функций
- •§ Теорема о вложенных промежутках (Коши-Кантора)
- •§ Теорема (Бореля-Лебега) о конечном покрытии.
- •§ Теорема о предельной точке
- •§ Критерий Коши
- •§ Теорема штольца
- •§ Односторонняя непрерывность
- •§ Классификация точек разрыва
- •§ Разрывы монотонной функции.
- •§ Гиперболические функции.
- •§. Равномерная непрерывность
- •Модуль непрерывности.
- •§. Функциональные уравнения
- •Раздел . Дифференциальное исчисление §. Дифференцируемость функции
- •§. Производная
- •§. Дифференциал
- •§. Производные и дифференциалы высших порядков
- •§.Таблица производных высших порядков
- •§. Правило Лейбница (нахождение производных высших порядков для функций заданных в виде произведения)
- •§. Логарифмическая производная
- •§. Высшие производные сложных функций
- •§. Дифференциалы высших порядков
- •§. Высшие производные функций заданных параметрически
- •§. Высшие производные обратных функций
- •§. Инвариантность формы первого дифференциала и неинвариантность формы высших дифференциалов функции
- •Раздел. Основные теоремы о дифференцируемых функциях
- •§. Формула и Многочлен Тейлора
- •§ Формула Тейлора с остаточным членом в форме Пеано
- •§ Остаточный член в форме Шлёмильха – Роша
- •§ Еще несколько полезных разложений.
- •§ Дифференцирование неравенств.
- •§ Необходимое и достаточное условие локального экстремума функции.
- •§. Достаточное условие экстремума.
- •§ Правило Лопиталя раскрытия неопределенностей.
- •§. Пример вычисления предела с помощью формулы Тейлора.
- •§ Выпуклость (вогнутость функций).
- •§ Некоторые замечательные неравенства математического анализа.
- •1. Неравенство Иенсена.
- •§ Применение производных к исследованию свойств функций и построению их графиков. Общая схема.
- •§ Примеры построения графиков функций.
- •§. Мнимая единица. Уявна одиниця. Imaginary Unit.
- •§. Поле комплексных чисел. Поле комплексних чисел.
- •§. Свойства элементов поля.
- •§ Тригонометрическая форма комплексного числа.
- •§ Извлечение корней натуральных степеней из комплексного числа.
- •§ Стереографическая проекция. Сфера Римана.
- •§ Формулы Эйлера.
- •§ Показательная форма записи комплексного числа. Логарифм в комплексной плоскости.
- •§. Функции с комплексными или вещественными аргументами и значениями. Графики. Последовательности.
- •§ Алгебраическая замкнутость поля комплексных чисел. Основная теорема алгебры.
- •§ Теорема Безу.
- •§ Разложение многочлена на множители в множестве комплексных чисел.
- •§. Комплексные корни многочлена с вещественными коэффициентами.
- •§ Решение алгебраических уравнений 1, 2, 3, 4 степени. Формулы Кардано. Метод Феррари.
- •§. Теорема Абеля.
- •§. Еще о функциях комплексного переменного.
- •Раздел. Неопределенный интеграл § Первообразная и неопределенный интеграл.
- •§ Замена переменной в неопределенном интеграле.
- •§. Интегрирование простейших (элементарных) дробей.
- •§. Интегрирование дробно-рациональных функций.
- •§. Метод Остроградского выделения рациональной части интеграла.
- •§. Интегрирование некоторых иррациональностей.
- •§. Интегрирование выражений, рациональным образом выражающихся через тригонометрические и гиперболические функции.
- •§ Эллиптические интегралы. Введение.
- •II. . Этим интегралом мы и займемся в следующем параграфе. §. Приведение интеграла к каноническому виду.
- •§. Эллиптические интегралы.
- •§. Интегралы, которые не могут быть выражены, через элементарные функции (не берущиеся интегралы ).
- •4. Интегральные синус и косинус: .
- •Элементы элементарной математики
- •Формулы сокращенного умножения. Метод интервалов решения дробно-рациональных (и не только!) неравенств.
- •Системы двух и трех линейных уравнений. Совместимость, определенность, неопределенность. Метод Гаусса исключения неизвестных.
- •Многочлены. Теорема Безу и ее следствия. Рациональные корни уравнений.
- •Степенная, показательная, логарифмическая функции. Основные свойства и графики. Решение показательных и логарифмических уравнений и неравенств.
- •Тригонометрические функции углового и числового аргументов. Определение и свойства. Обратные тригонометрические функции. Формулы двойного и половинного аргумента. Формулы приведения.
- •Решение простейших (и не только!) тригонометрических уравнений и неравенств.
- •Построение графиков функций с помощью элементарных движений. Общая схема исследование функций с помощью производной.
- •Метод сечений при решении задач с параметром. Задачи, связанные с исследованием функций.
- •§10. Векторы, операции над ними. Скалярное, векторное и смешанное произведение. Проекции векторов. Примеры использования векторов в задачах физики.
- •§11. Уравнение прямой на плоскости в векторной форме.
- •Варианты контрольных работ
- •Дополнение 1 Вещественные числа
- •Сечения множества рациональных чисел
- •Перерізи множини раціональних чисел.
- •Сравнение сечений множества рациональных чисел
- •Порівняння перерізів множними раціональних чисел.
- •Теоремы об аппроксимации вещественных чисел рациональными
- •Теореми про апроксимацію дійсних чисел раціональними.
- •Теорема Дедекинда (непрерывность множества вещественных чисел)
- •Теорема Дедекінда (непрерівність множини дійсних чисел).
- •Сложение вещественных чисел
- •Додавання дійсних чисел
- •Произведение вещественных чисел
- •Дополнение 2 Исчисление высказываний
- •II. Правила построения формул ив.
- •III. Правила вывода ив
- •IV. Аксиомы ив.
- •V.Вывод
- •VI .Интерпретации
- •Математическая логика. Mathematical Logic Математична логіка
- •Формальный язык (аксиоматическая теория) и метаязык
- •Знаки, знакосочетания, алфавит.
- •Знаки, знакосполучення, алфавіт
- •Операции над словами
- •Операції над словами.
- •Выражения формального языка
- •Вирази формальної мови
- •Структурные знаки формального языка
- •Структурні знаки формальної мови
- •Переменные и константы (постоянные)
- •Зминні та сталі (константи)
- •Дополнение 3 Теорема про граничный переход в равенстве.
- •Дополнение 4 § теория пределов
- •Непрерывность и дифференцируемость
Системы двух и трех линейных уравнений. Совместимость, определенность, неопределенность. Метод Гаусса исключения неизвестных.
Теория.
Произвольная система линейных уравнений называется совместной, если она имеет решения, и не совместной в противном случае. При этом совместная система линейных уравнений называется определенной, если она имеет единственное решение, и не определенной если она имеет более одного ( а именно бесконечно много) решений.
Для системы двух линейных уравнений с двумя неизвестными исследование на совместность производится очень просто.
Если
задана система
![]() ,
то:
,
то:
а)
если
![]() ,
то система совместна и определена, т.е.
имеет единственное решение;
,
то система совместна и определена, т.е.
имеет единственное решение;
б)
если
![]() ,
то система не совместна, т.е. не имеет
решений;
,
то система не совместна, т.е. не имеет
решений;
в)
если
![]() ,
то система совместна и не определена,
т.е. имеет бесконечно много решений;
,
то система совместна и не определена,
т.е. имеет бесконечно много решений;
Для систем линейных уравнений с количеством неизвестных более двух исследование на совместность более сложно и будет изучено позднее.
Основным методом решения систем линейных уравнений является метод Гаусса исключения неизвестных, который, при некоторой модификации, позволяет как исследовать систему на совместность – не совместность, так и, в случае совместности, найти решения как определенных так и не определенных систем.
Задачи для решения :1*, 2*, …, 15*
Исследовать на совместность и решить системы линейных уравнений с двумя неизвестными:
1*.
![]() ;
2*.
;
2*.
![]() ;
;
3*.
![]() ;
4*.
;
4*.
![]() ;
;
5*.
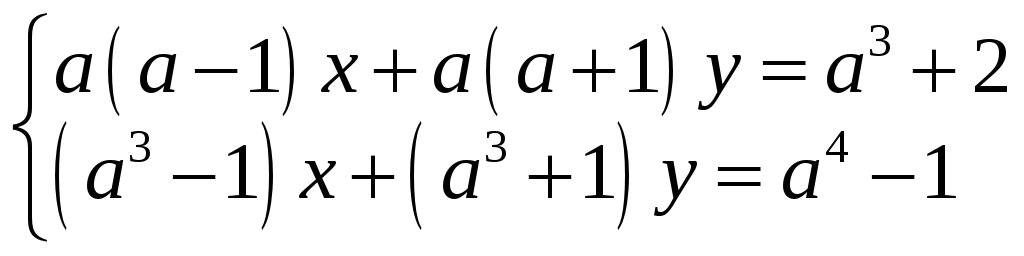 ;
;
6*.
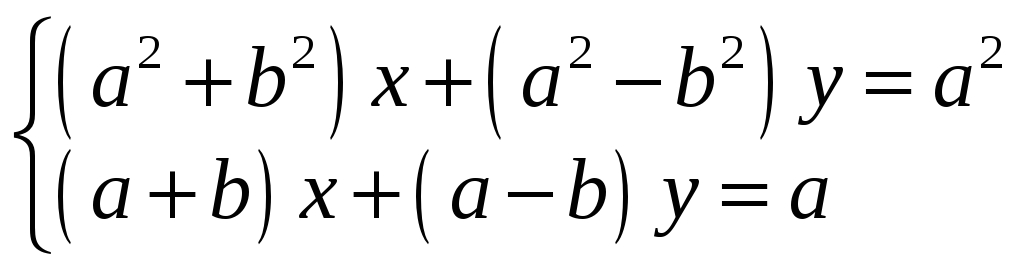 .
.
7*.
Числа a и b
таковы, что система
![]() имеет единственное решение х =
1, у = 1. Найти a
и b.
имеет единственное решение х =
1, у = 1. Найти a
и b.
8*.
При каких a и b
система
![]() имеет бесконечно много решений?
имеет бесконечно много решений?
9*.
При каких a
система
![]() не имеет решений?
не имеет решений?
10*. Числа a, b и с таковы, что система
![]() имеет бесконечно
много решений,
имеет бесконечно
много решений,
причем х = 1, у = 3, одно из них. Найти a и b.
11*. Найти все такие значения а, чтобы при любом b, нашлось такие с при которых система имеет хотя бы одно решение:
а)
![]() ;
б)
;
б)
![]() .
.
Решить системы линейных уравнений методом Гаусса исключения неизвестных:
12*.
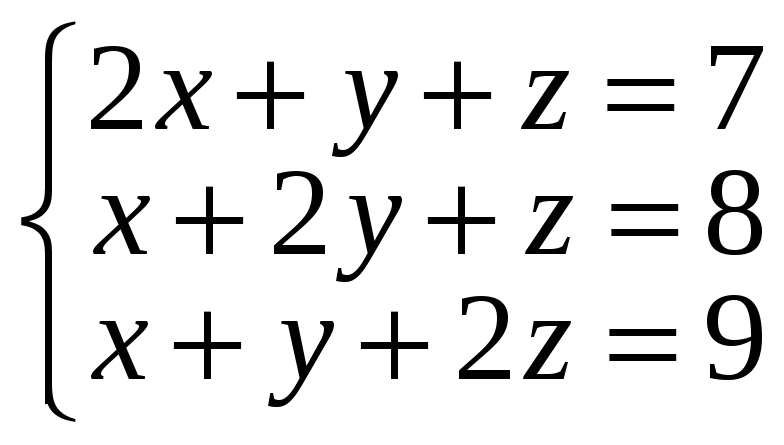 ;
13*.
;
13*.
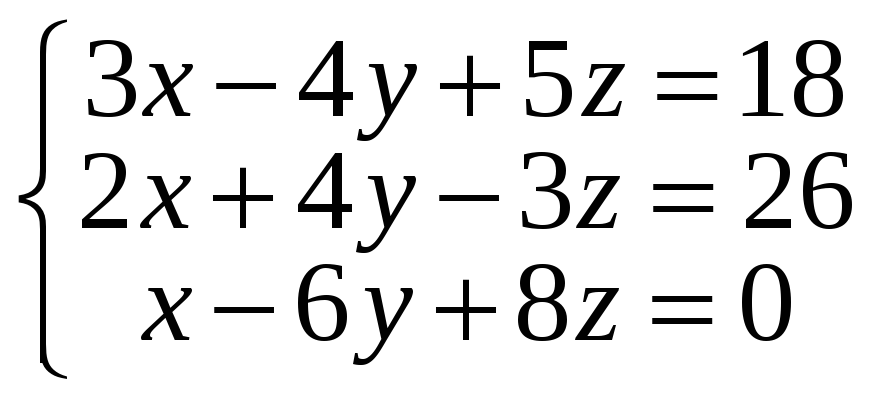 ;
;
14*.
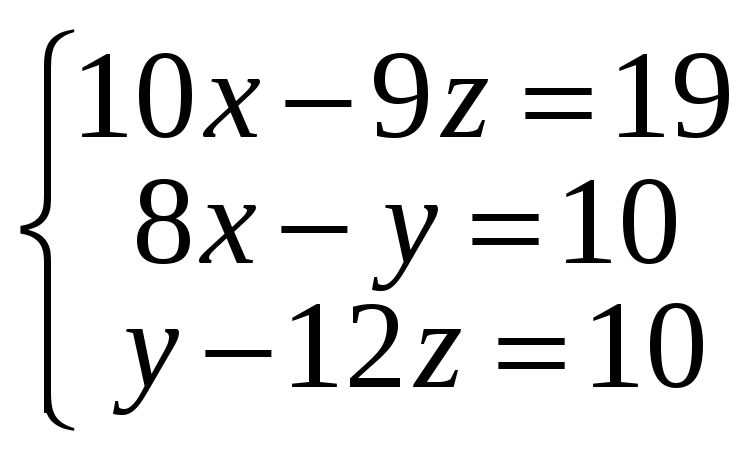 ;
15*.
;
15*.
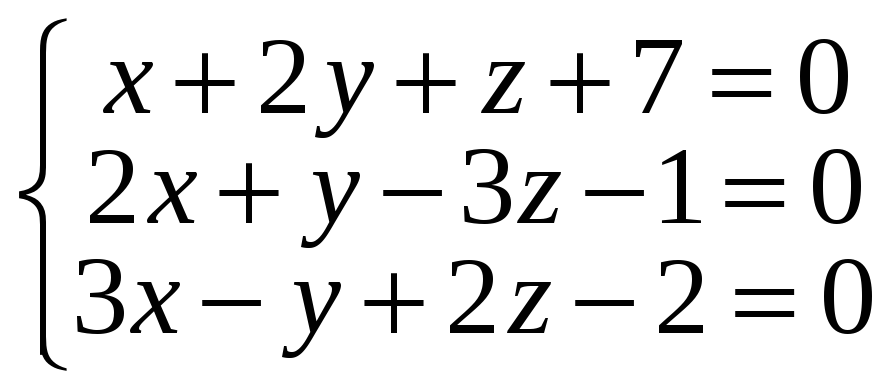 .
.
4.
Многочлены. Теорема Безу и ее следствия. Рациональные корни уравнений.
Схема Горнера. Возвратные уравнения.
Теория.
Алгебраическим
полиномом степени
![]() называется конструкция вида:
называется конструкция вида:
![]() .
.
Пусть
заданы алгебраические полиномы:
![]() и
и
![]() ,
причем
,
причем
![]() .
Тогда существуют два других полинома
– один
.
Тогда существуют два других полинома
– один
![]() степени
степени![]() ,
другой
,
другой
![]() – степени, не превышающей числа
– степени, не превышающей числа
![]() ,
такие что
,
такие что
![]() .
Полином
.
Полином
![]() называется неполным частным от деления
полинома
называется неполным частным от деления
полинома
![]() на полином
на полином
![]() ,
а полином
,
а полином
![]() остатком от такого деления. Если, при
этом,
остатком от такого деления. Если, при
этом,
![]() то говорят, что полином
то говорят, что полином
![]() делится на полином
делится на полином
![]() без остатка, а полином
без остатка, а полином
![]() называется полным частным, или просто
частным от деления полинома
называется полным частным, или просто
частным от деления полинома
![]() на полином
на полином
![]() .
.
В
случае
![]() приведенная формула имеет вид
приведенная формула имеет вид
![]() .
.
Т.
(Безу) Остаток от деления полинома
![]() на двучлен
на двучлен
![]() равен значению полинома
равен значению полинома
![]() в точке
в точке
![]() ,
т.е.
,
т.е.
![]() .
.
Т.
( следствие из т
Безу) Полином
![]() делится на двучлен
делится на двучлен
![]() тогда и только тогда когда
тогда и только тогда когда
![]() является корнем полинома
является корнем полинома
![]() .
.
Т.
( следствие из т
Безу) Если
![]() является корнем полинома
является корнем полинома
![]() ,
т.е.
,
т.е.
![]() то
то
![]() .
.
Это следствие из теоремы Безу позволяет многочлен с известными (полностью или частично) корнями разложить на множители.
Т.
Если алгебраическое уравнение
![]() имеет целые коэффициенты
имеет целые коэффициенты
![]() и рациональное число
и рациональное число
![]() является его корнем, то число
является его корнем, то число
![]() является делителем свободного члена
уравнения, а число
является делителем свободного члена
уравнения, а число
![]() является делителем старшего коэффициента
уравнения.
является делителем старшего коэффициента
уравнения.
Это утверждение позволяет из всего множества рациональных чисел сразу отобрать только те, которые могут быть корнями уравнения. Установить, являются ли они корнями уравнения можно непосредственной подстановкой. При этом, удобно значение полинома в точке вычислить способом, который предложенным Горнером. Проиллюстрируем схему Горнера на конкретном примере (это верно передает суть метода и не загромождает выкладку).
Полином
![]() запишем в виде, предложенном Горнером:
запишем в виде, предложенном Горнером:
![]() .
.
Запись,
стоящая справа позволяет вычислить
значение полинома
![]() -й
степени в точке не более чем за
-й
степени в точке не более чем за
![]() операций. Оказывается это самый
экономичный способ вычисления значения
полинома в точке. На основе такой записи
полинома можно построить вычислительную
табличку, которая, зачастую, также
называется схемой Горнера.
операций. Оказывается это самый
экономичный способ вычисления значения
полинома в точке. На основе такой записи
полинома можно построить вычислительную
табличку, которая, зачастую, также
называется схемой Горнера.
В верхней строке таблицы ( кроме первой клетки) записываются коэффициенты исходного полинома в порядке убывания степеней. В первой клетке нижней строки таблицы записывается значение аргумента, при котором вычисляется значение полинома. Остальные клетки нижней строки заполним по формулам:
![]() .
.
-
–
an
an-1
an-2
… …
a2
a1
a0
c
bn-1
bn-2
bn-3
… …
b1
b0
R
Заполнив
табличку, отметим что в последней клетке
нижней строки стоит
![]() – значение полинома в точке
– значение полинома в точке
![]() .
В клетках нижней строки, кроме первой
и последней, стоят коэффициенты частного
от деления исходного полинома на двучлен
.
В клетках нижней строки, кроме первой
и последней, стоят коэффициенты частного
от деления исходного полинома на двучлен
![]() .
.
Для
полинома
![]() и
и
![]() вычисляя значение полинома в точке
вычисляя значение полинома в точке
![]() получаем:
получаем:
-
2
3
-7
-5
4
-2
2
-1
-5
5
-6
Т.
е. установлено что
![]() .
.
Задачи для решения :1*, 2*, …, 21*
Решить алгебраические уравнения:
1*.
![]() ;
2*.
;
2*.
![]() ;
;
3*.
![]() ;
4*.
;
4*.
![]() ;
;
5*.
![]() ;
;
6*. Найти сумму коэффициентов многочлена:
![]() .
.
7*.
Делится ли многочлен
![]() на
на![]()
8*.
Найти остаток от деления
![]() на
на
![]() .
.
9*.
Некоторый многочлен при делении на
![]() дает в остатке 5, а при делении на
дает в остатке 5, а при делении на
![]() дает в остатке 3. Найти остаток от деления
того же многочлена на
дает в остатке 3. Найти остаток от деления
того же многочлена на
![]() .
.
10*.
Остаток от деления
![]() на
на
![]() равен 35, а от деления на
равен 35, а от деления на
![]() остаток равен 320. Найти а и с.
остаток равен 320. Найти а и с.
С помощью схемы Горнера решить следующие уравнения:
11*.
![]() ,
,
12*.
![]() ,
,
13*.
![]() ,
,
14*.
![]() .
.
Решить возвратные уравнения:
15*.
![]() ,
,
16*.
![]() ,
,
17*.
![]() ,
,
18*.
![]() .
.
19*. Решить следующие уравнения разложив левую часть в произведение двух квадратных трехчленов:
а)
![]() ,
б)
,
б)
![]() .
.
20*.
Найти а при которых уравнение
![]() имеет
два совпадающих корня.
имеет
два совпадающих корня.
21*.
Число
![]() является корнем уравнения
является корнем уравнения
![]() .
.
Найти остальные корни, зная что а и b рациональные числа.
5.
