§ Гиперболические функции.

Каждая тригонометрическая функция имеет свой гиперболический аналог.

.

.

, .

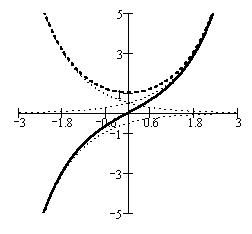
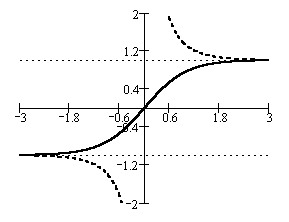
На рисунке слева приводятся графики гиперболических синуса (сплошная линия) и косинуса (пунктирная линия). Тонкой пунктирной линией построен график функции и симметричные ему относительно оси абсцисс и оси ординат.

На рисунке справа приводятся графики гиперболических тангенса (сплошная линия) и котангенса (пунктирная линия). Тонкой пунктирной линией построен график функций .

Для всех введенных гиперболических функций ( для y = ch x отдельно для х > 0 и отдельно для x < 0) существуют обратные функции.

Найдем обратные функции к гиперболическим функциям:

1.  

  .

2.  

 ()  .

Получили две однозначные ветви обратной функции.

3. 

= ( если ).

4.    ( если ).

5. Из 3. и 4. : .

Ниже приводятся графики обратных гиперболических функций

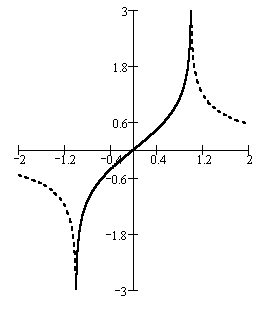
Слева приведены графики функций обратных гиперболическому синусу ( сплошной линией) и косинусу (пунктирной линией), причем во втором случае приводятся обе ветви одна выше а другая ниже оси абсцисс .

Справа приведены графики функций обратных гиперболическому тангенсу ( сплошной линией) и котангенсу (пунктирной линией) .

§. Равномерная непрерывность

Def. Функция называется равномерно непрерывной на множестве Х, если

.

Из определения равномерной непрерывности функции на множестве следует, что функция непрерывна в каждой точке этого множества, но не наоборот.

Примеры:

1. . Функция- непрерывна на . Однако ,

т.е. не является равномерно непрерывной на промежутке .

2. , Функция - непрерывна на . Но, если положить

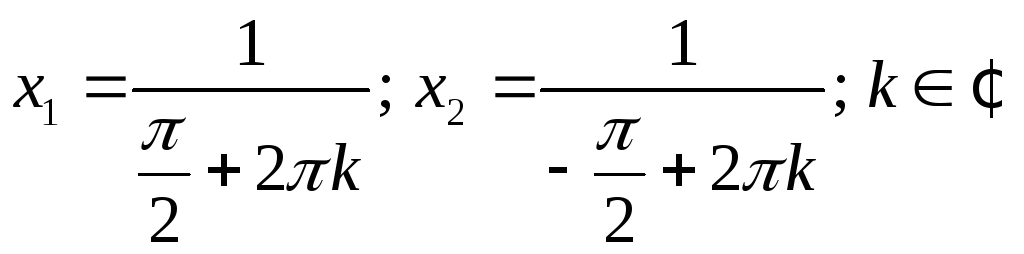то получим:

,

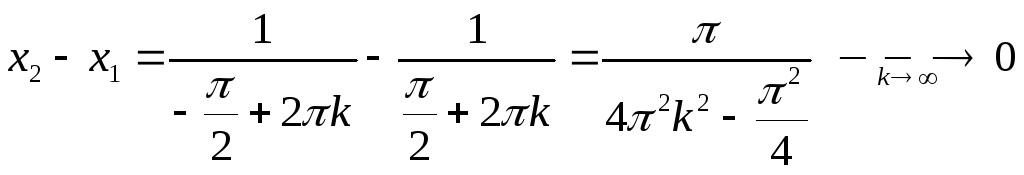и при этом: .

Из этого делаем заключение о том, что функция не является равномерно непрерывной на .

Т Кантора (о равномерной непрерывности). Если функция непрерывна на замкнутом промежутке то она равномерно непрерывна на нём.

∆ Пусть функция непрерывна на замкнутом промежутке . Тогда :

.

Множество всех дельта-окрестностей точек промежутка образует открытое покрытие замкнутого промежутка . Выделив из этого покрытия конечное подпокрытие получим : - конечное подпокрытие.

Положим . Тогда :

 

.▲

Колебание функции.

Def. Колебанием функции на D( f ) называется , причем

.

Def. Колебанием функции на множестве М называется: .

Очевидно при сужении множества колебание функции не увеличивается.

Рассмотрим

т.е. колебание функции при уменьшении не увеличивается и ограничено снизу. Значит:

Величина называется колебанием функции в точке .

Т. Функция - непрерывна в точке x = a тогда и только тогда когда .

∆ Пусть - непрерывна в точке x = a. 

т.е. . ▲

Если то величина 'называется финальным колебанием функции в т. x = a.

Т. Функция имеет конечный предел в точке x = a тогда и только тогда, когда ее финальное колебание в точке x = a равно 0 т.е. . ∆▲