§. Метод Остроградского выделения рациональной части интеграла.
Теорема.
Если правильная дробь
имеет знаменатель, представленный в
виде
,
то:
.
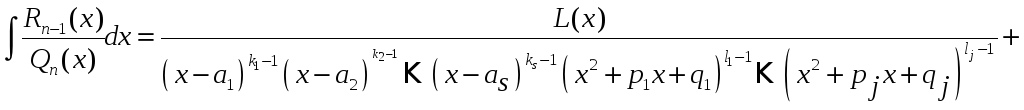
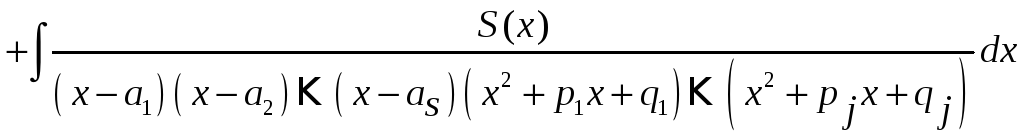Здесь L(x) и S(x) многочлены на степень ниже, чем многочлены, стоящие в соответствующих знаменателях. Интеграл, стоящий в правой части можно взять методом разложения дроби в сумму простейших дробей (и, что очень важно) интегралов IV типа среди них не будет.
Если
разложение
на множители неизвестно, то:
.
Примеры.
1.
Вычислить
.
можно найти с
помощью алгоритма Евклида.
;
От деления на 2 наибольший общий делитель
двух полиномов не изменится
.
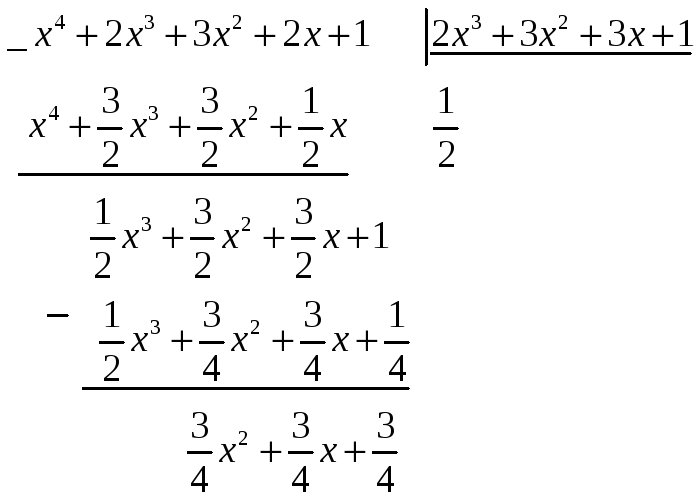
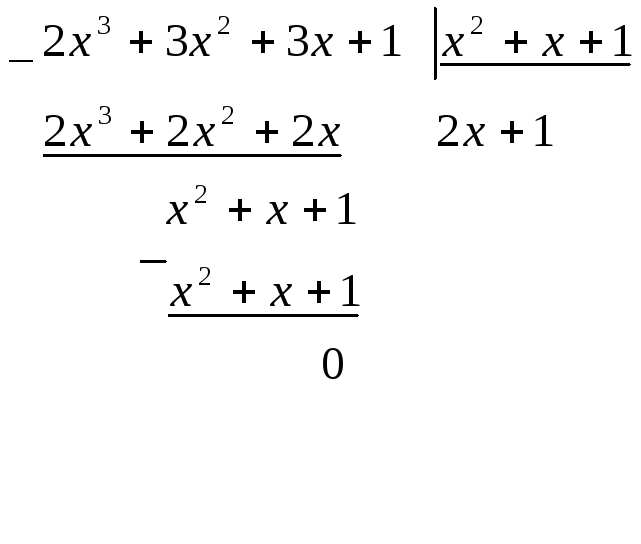
Наибольший
общий делитель знаменателя и его
производной
.
Тогда:
.
Для нахождения A, B, C, D продифференцируем обе части:
.
и числители дробей должны совпадать.
.
Приравниваем
коэффициенты при соответствующих
степенях
.
.
Для исходного интеграла получаем:
.
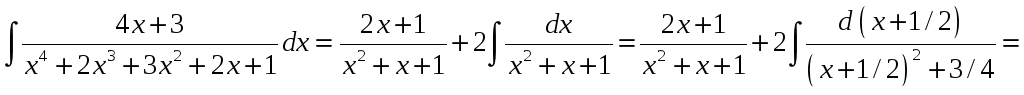
2.
;
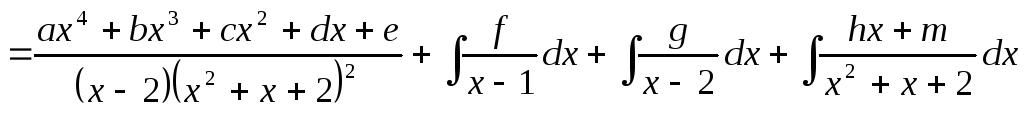продифференцировав
обе части равенства, получим систему
для нахождения неопределенных
коэффициентов
.
Остроумие метода Остроградского состоит
в получении вне интегральной дроби без
интегрирования, а с помощью решения
системы линейных уравнений.
§. Интегрирование некоторых иррациональностей.
А.
Дробно-линейные иррациональности
.
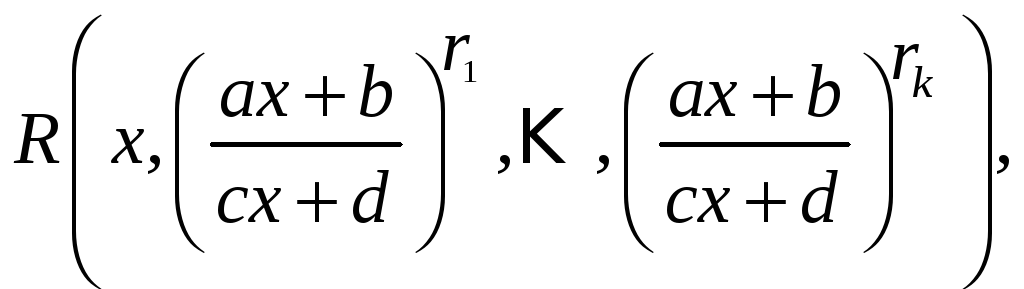
Записав
( N-общий знаменатель дробей
),
получим:
=
.
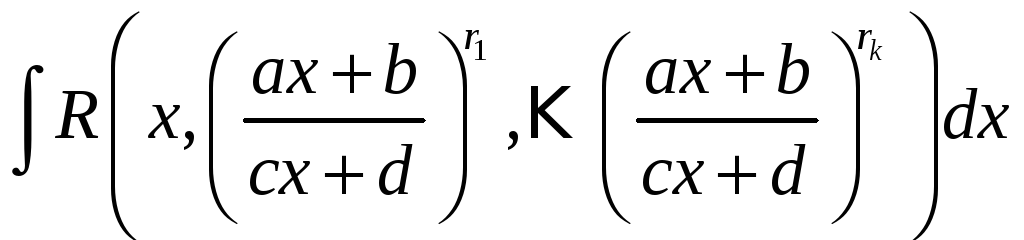
Получен интеграл от рациональной функции.
Примеры:
1.
.
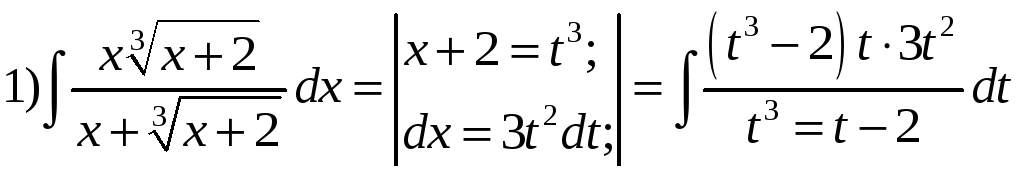2.
=
=
=
.
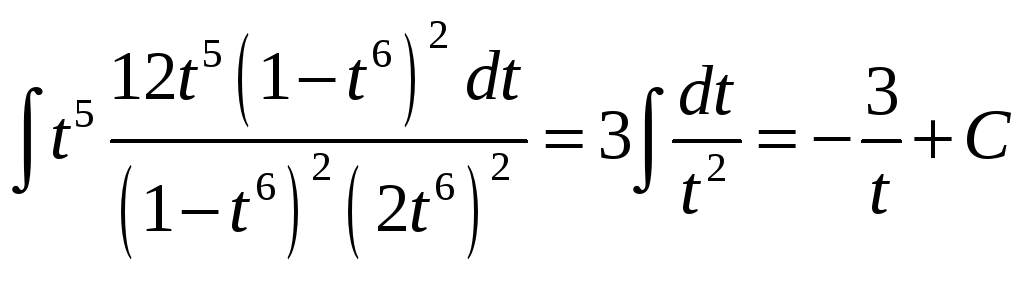Возвращаясь к исходной переменной, получим:
=
.
Б. Интегрирование дифференциального бинома (биномиального дифференциала):
.
Теорема
Чебышева: Если
,то интеграл от дифференциального бинома
выражается через элементарные функции
тогда и только тогда когда:
1.
–
целое; 2.
– целое; 3.
– целое.
и при этом следующие подстановки (Чебышева) сводят интегралы к интегралам от рациональных функций.
,где s – общий
знаменатель дробей m и n,
,
s – знаменатель дроби p,
, s – знаменатель
дроби p.
Примеры:
1.
=
=
=
=
=
.
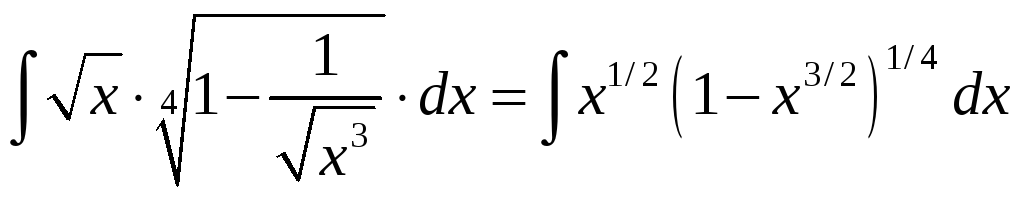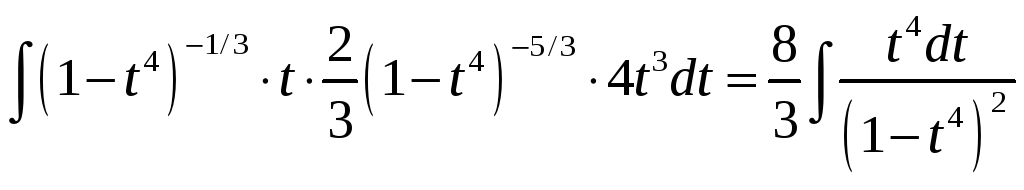С помощью второй подстановки Чебышева интеграл от дифференциального бинома стал интегралом от рациональной функции.
2.
=
.
Ни одна из подстановок Чебышева не
подходит – интеграл не может быть
выражен через элементарные функции (не
берётся).
3.
= …
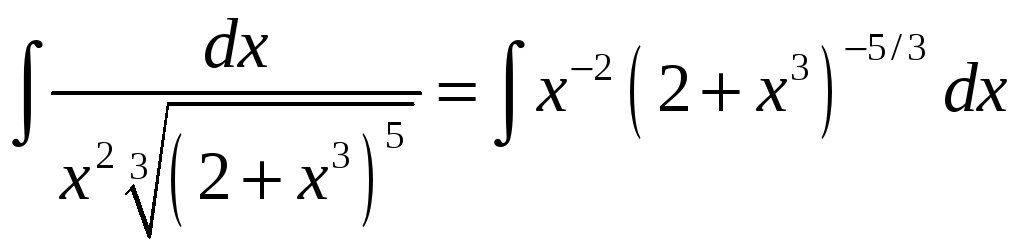В
данном случае
и, следовательно, третья подстановка
Чебышева должна рационализовать
подынтегральное выражение.
В
самом деле
,
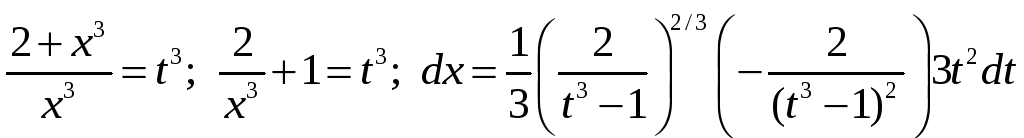и получается интеграл
… =
=
,
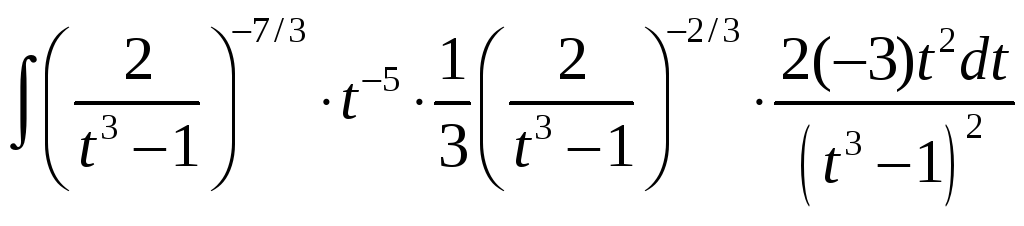и интеграл рационализован.
4.
= …
Здесь
и
выполняя замену
, получим
… =
.
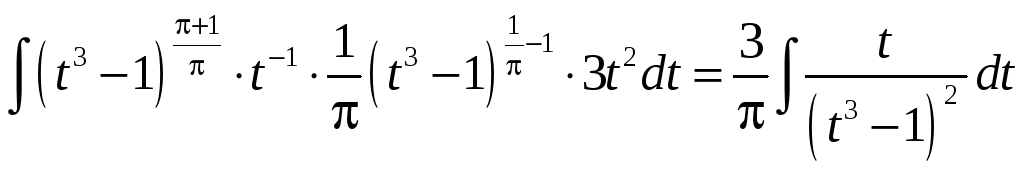Приведенный пример показывает что для не рациональных показателей степеней подстановки Чебышева тоже могут быть полезны.
В.
Подстановки Эйлера :
;
Для интегрирования квадратичных иррациональностей
I.
II.
;
III
.
.
Других
случаев просто нет, ибо тогда
.
Знаки плюс–минус выбираются из
соображений удобства. Остроумие
подстановок Эйлера заключается в том,
что для нахождения х получается
линейное уравнение.
1.
… Учитывая что
,
выполним первую подстановку Эйлера.
… =
=
=
.
Полученные интегралы от рациональных функций трудностей не представляют.
2.
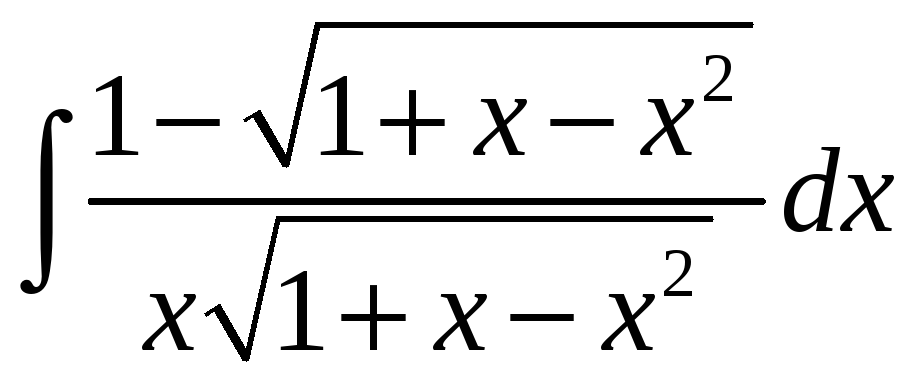= … Учитывая что
,
выполним вторую подстановку Эйлера.
.
Тогда … =
.
Вновь получен интеграл от рациональной функции.
3.
= … Квадратный трехчлен под знаком
корня имеет вещественные корни
поэтому можно применить третью подстановку
Эйлера.
и получаем
=
, а это интеграл от рациональной функции.
Г.
Интегрирование иррациональностей
вида :
.
Введем
обозначение
.
Г1.
.
Для нахождения
коэффициентов
и
продифференцируем обе части равенства:
в левой части
перейдем к к общему знаменателю:
.
Многочлены стоящие в числителях дробей
справа и слева от знака равенства должны
быть равны и, следовательно, должны быть
равны коэффициенты при соответствующих
степенях переменной. Отсюда получаем
систему линейных уравнений для нахождения
коэффициентов
и
.
Пример: 1.
= …
Г2.
…
Замена
;
;
;
=
=
=
=
=
.
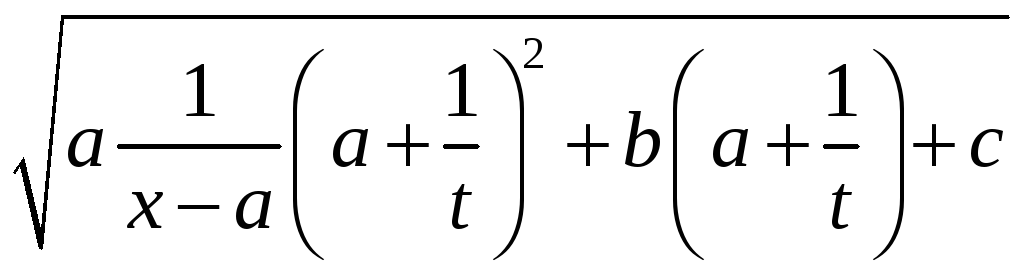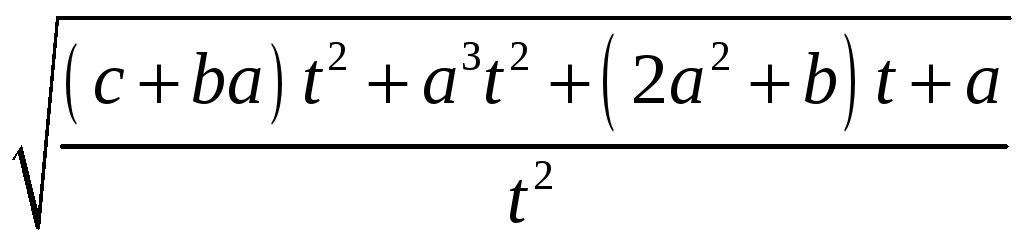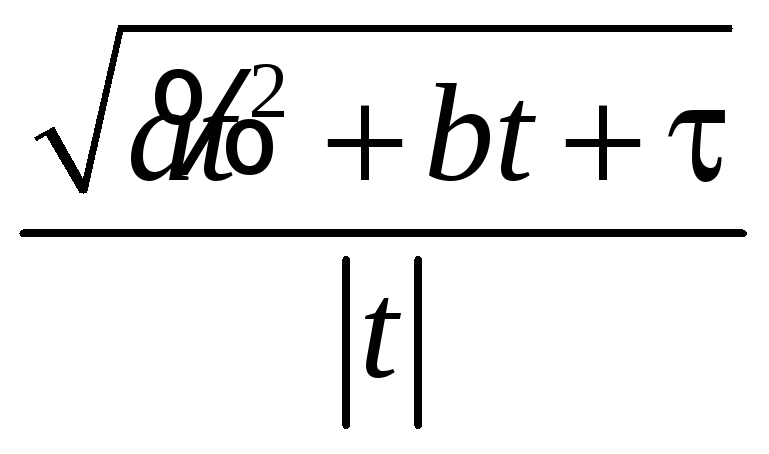После замены переменной, получим
… =
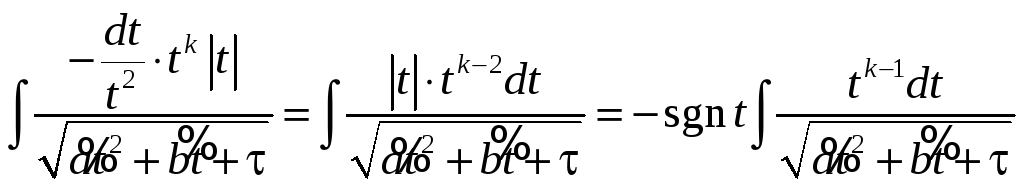– а такой интеграл рассмотрен в
предыдущем пункте.
Пример:
= … .
Г3.
= …
Подстановка Абеля:
;
;
=
(*).
Находя дифференциал от правой и левой части равенства (*), получим:
;
;
;
а возводя правую и левую части равенства (*) в квадрат, будем иметь:
;
.
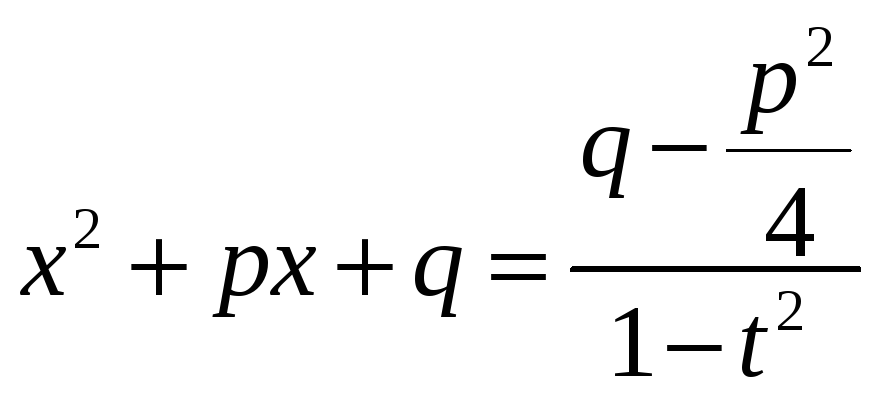Т.е. после выполнения подстановки Абеля, исходный интеграл станет интегралом от рациональной функции:
… =
.
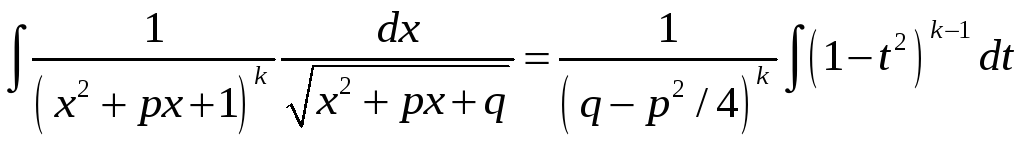Г4.
.
В первом интеграле
делаем замену:
,
а во втором
и задача интегрирования интеграла типа
Г4 сведена к
интегрированию рациональных функций.
Г5.
= … .
Возможны варианты:
а)
и
;
тогда получим интеграл, рассмотренный
в пункте Г3, и
применим подстановку Абеля.
б)
и
тогда
;
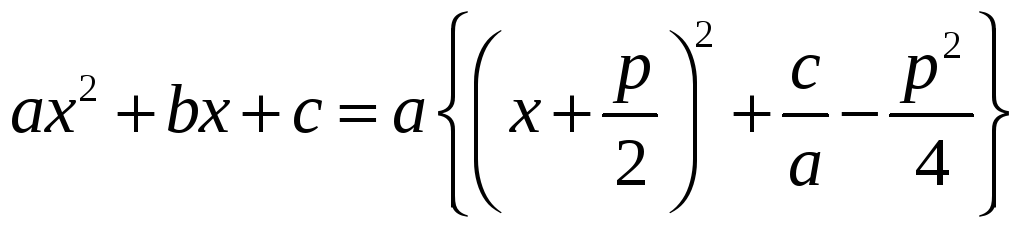и после замены
у квадратных трехчленов не останется
первых степеней (интегралы типа Г4).
в)
В случае
сделаем дробно-линейную подстановку
,
(
).
Тогда
=
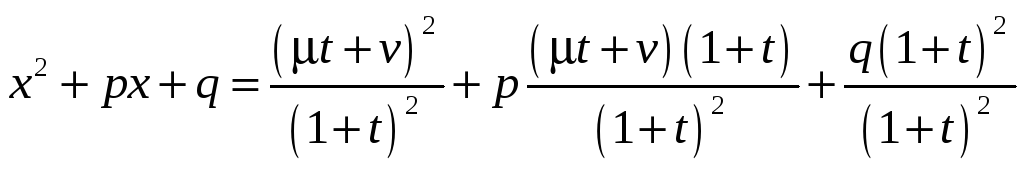и потребуем, чтобы коэффициент при
первой степени t равнялся нулю:
.
Аналогично,
для
:
.
Из
двух полученных уравнений находим
и
=
;
и,
следовательно:
;
.
Таким
образом
и
есть корни квадратного уравнения:
.
После замены
в квадратных трехчленах не остается
первых степеней (интегралы типа Г4).