§ Правило Лопиталя раскрытия неопределенностей.

Т. Если функции f (x) и g(x) дифференцируемы в проколотой окрестности некоторой точки на расширенной числовой прямой, где производная второй из них отлична от нуля и в т. : 1) либо , 2) либо .

Тогда . Знак означает что, если предел, стоящий справа от этого знака существует и конечен, то существует, конечен и равен ему и предел стоящий слева от знака.

 Ограничимся доказательством в случае

1). . Доопределим функции f (x) и g(x) в точке следующим образом: f () = 0; g() = 0. Тогда, по теореме Коши: .

Отсюда следует утверждение теоремы. При х   замена t = 1/x позволяет свести доказательство к только что проведенному. ▲

§. Пример вычисления предела с помощью формулы Тейлора.

При вычислении предела воспользуемся разложением числителя и знаменателя в ряд Тейлора:

.

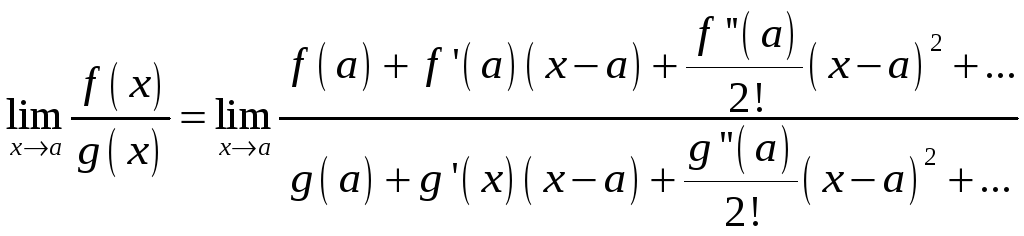Проанализируем записанную формулу.

*. Если , то предел равен .

*. Если , то предел равен нулю.

*. Если , то предел равен бесконечности.

*. Если , то, сокращая числитель и знаменатель дроби на , выясняем, что:

**. Если , то предел равен , что равносильно применению

правила Лопиталя.

**. Если , то предел равен нулю.

**. Если , то предел равен бесконечности.

**. Если , то, сокращая числитель и знаменатель дроби еще раз на , выясняем, что:

***. Если , то предел равен , что равносильно повторному применению правила Лопиталя.

***. Если , то предел равен нулю.

***. Если , то предел равен бесконечности.

***. Если , то, …. ….. …. .

Таким образом ясно, что применение правила Лопиталя и использование разложения функций в ряды Тейлора по сути одно и тоже (с естественными оговорками по поводу дифференцируемости).

Практический совет: Если функции, стоящие в числителе и знаменателе дроби имеют известные разложения в ряды Тейлора или эти разложения могут быть легко получены, то следует этим воспользоваться. Если же получение вышеупомянутых разложений связано со значительными техническими трудностями, то более рациональным является применение правила Лопиталя.

Пример.

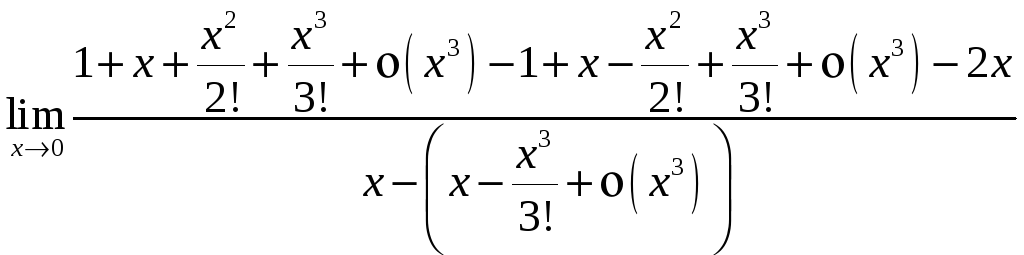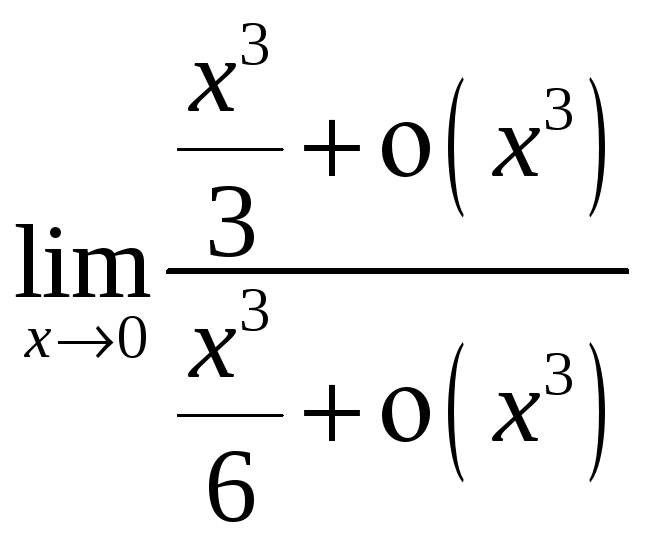= = = 0.

§ Выпуклость (вогнутость функций).

Def: Определенная на промежутке I функция f (x) называется выпуклой (вогнутой) если ее дуга не ниже (не выше) стягивающей ее хорды.

.

Знак неравенства в заключении говорит о характере выпуклости (вогнутости).

(>) – строгая выпуклость, () – не строгая выпуклость,

(<) – строгая вогнутость, () – не строгая вогнутость.

*. Дуга функции f (x) выпуклой на промежутке I лежит ниже касательной к графику функции в произвольной внутренней точке промежутка I .

*. Дуга функции f (x) вогнутой на промежутке I лежит выше касательной к графику функции в произвольной внутренней точке промежутка I .

*. Для выпуклой функции угловой коэффициент хорды не возрастает при возрастании абсциссы правого конца хорды (эквивалент определения выпуклости).

Для выпуклой функции:

 .

Производная выпуклой функции на промежутке не убывает.

*. Для вогнутой функции угловой коэффициент хорды не убывает при возрастании абсциссы правого конца хорды (эквивалент определения вогнутости).

Для вогнутой функции:

 .

Производная вогнутой функции на промежутке не возрастает.

Def. Точками перегиба графика функции называются точки, разделяющие смежные промежутки с противоположными направлениями выпуклости.

*. Дуги с разнонаправленной выпуклостью, разделяемые точкой перегиба, лежат по разные стороны от касательной в точке перегиба т.к. в точке перегиба дуга графика пересекает касательную.