
- •Формула называется формулой с тесными отрицаниями, если в ней нет связок þ и û, и отрицания относятся только к пропозициональным переменным.
- •§ Кванторы
- •§ Элементы теории множеств
- •§ Операции над множествами
- •§ Операции соответствия между множествами
- •Физические типы соответствий:
- •Def: Множества, равномощные множеству точек, принадлежащих интервалу (0, 1) называются множествами мощности континиум. Пример: Множество вещественных чисел r является множеством мощности континиум.
- •Раздел 2. Предел и непрерывность § грани числовых множеств
- •§ Расположение точек относительно множества
- •§ Предел функции по коши Рассматриваются числовые функции числового аргумента:
- •Запишем еще раз определение предела функции на языке e-d:
- •Внимательно рассмотрев определение предела нетрудно установить, что:
- •Запишем теперь сокращенное определение того, что f (X) ® b при X ® а на языке e-d:
- •Словарик
- •§ Непрерывность функции
- •§ Непрерывность элементарных функций
- •Примеры элементарных функций:
- •§ Предел последовательности
- •Примеры:
- •Раздел 3. Бесконечно малые и др. Величины § определения, терминология и примеры
- •Раздел 4. Непрерывные функции
- •§ Частичные пределы
- •§ Предельный переход в равенствах и неравенствах
- •§ Непрерывность тригонометрических функций
- •Раздел 5. Замечательные пределы § Первый замечательный предел
- •§ Арифметические действия над монотонными функциями.
- •§ Бином Ньютона
- •§ Предел функции по гейне ( по последовательности)
- •§ Второй замечательный предел
- •§ НепрЕрывность показательной функции
- •§ НепрЕрывность логарифмической функции
- •§ Пределы, связанные с показательными, логарифмическими и степенными функциями
- •§ Степенные асимптотические разложения
- •§ Действия над асимптотическими разложениями.
- •§ Асимптотические разложения Маклорена для основных элементарных функций
- •§ Теорема о вложенных промежутках (Коши-Кантора)
- •§ Теорема (Бореля-Лебега) о конечном покрытии.
- •§ Теорема о предельной точке
- •§ Критерий Коши
- •§ Теорема штольца
- •§ Односторонняя непрерывность
- •§ Классификация точек разрыва
- •§ Разрывы монотонной функции.
- •§ Гиперболические функции.
- •§. Равномерная непрерывность
- •Модуль непрерывности.
- •§. Функциональные уравнения
- •Раздел . Дифференциальное исчисление §. Дифференцируемость функции
- •§. Производная
- •§. Дифференциал
- •§. Производные и дифференциалы высших порядков
- •§.Таблица производных высших порядков
- •§. Правило Лейбница (нахождение производных высших порядков для функций заданных в виде произведения)
- •§. Логарифмическая производная
- •§. Высшие производные сложных функций
- •§. Дифференциалы высших порядков
- •§. Высшие производные функций заданных параметрически
- •§. Высшие производные обратных функций
- •§. Инвариантность формы первого дифференциала и неинвариантность формы высших дифференциалов функции
- •Раздел. Основные теоремы о дифференцируемых функциях
- •§. Формула и Многочлен Тейлора
- •§ Формула Тейлора с остаточным членом в форме Пеано
- •§ Остаточный член в форме Шлёмильха – Роша
- •§ Еще несколько полезных разложений.
- •§ Дифференцирование неравенств.
- •§ Необходимое и достаточное условие локального экстремума функции.
- •§. Достаточное условие экстремума.
- •§ Правило Лопиталя раскрытия неопределенностей.
- •§. Пример вычисления предела с помощью формулы Тейлора.
- •§ Выпуклость (вогнутость функций).
- •§ Некоторые замечательные неравенства математического анализа.
- •1. Неравенство Иенсена.
- •§ Применение производных к исследованию свойств функций и построению их графиков. Общая схема.
- •§ Примеры построения графиков функций.
- •§. Мнимая единица. Уявна одиниця. Imaginary Unit.
- •§. Поле комплексных чисел. Поле комплексних чисел.
- •§. Свойства элементов поля.
- •§ Тригонометрическая форма комплексного числа.
- •§ Извлечение корней натуральных степеней из комплексного числа.
- •§ Стереографическая проекция. Сфера Римана.
- •§ Формулы Эйлера.
- •§ Показательная форма записи комплексного числа. Логарифм в комплексной плоскости.
- •§. Функции с комплексными или вещественными аргументами и значениями. Графики. Последовательности.
- •§ Алгебраическая замкнутость поля комплексных чисел. Основная теорема алгебры.
- •§ Теорема Безу.
- •§ Разложение многочлена на множители в множестве комплексных чисел.
- •§. Комплексные корни многочлена с вещественными коэффициентами.
- •§ Решение алгебраических уравнений 1, 2, 3, 4 степени. Формулы Кардано. Метод Феррари.
- •§. Теорема Абеля.
- •§. Еще о функциях комплексного переменного.
- •Раздел. Неопределенный интеграл § Первообразная и неопределенный интеграл.
- •§ Замена переменной в неопределенном интеграле.
- •§. Интегрирование простейших (элементарных) дробей.
- •§. Интегрирование дробно-рациональных функций.
- •§. Метод Остроградского выделения рациональной части интеграла.
- •§. Интегрирование некоторых иррациональностей.
- •§. Интегрирование выражений, рациональным образом выражающихся через тригонометрические и гиперболические функции.
- •§ Эллиптические интегралы. Введение.
- •II. . Этим интегралом мы и займемся в следующем параграфе. §. Приведение интеграла к каноническому виду.
- •§. Эллиптические интегралы.
- •§. Интегралы, которые не могут быть выражены, через элементарные функции (не берущиеся интегралы ).
- •4. Интегральные синус и косинус: .
- •Элементы элементарной математики
- •Формулы сокращенного умножения. Метод интервалов решения дробно-рациональных (и не только!) неравенств.
- •Системы двух и трех линейных уравнений. Совместимость, определенность, неопределенность. Метод Гаусса исключения неизвестных.
- •Многочлены. Теорема Безу и ее следствия. Рациональные корни уравнений.
- •Степенная, показательная, логарифмическая функции. Основные свойства и графики. Решение показательных и логарифмических уравнений и неравенств.
- •Тригонометрические функции углового и числового аргументов. Определение и свойства. Обратные тригонометрические функции. Формулы двойного и половинного аргумента. Формулы приведения.
- •Решение простейших (и не только!) тригонометрических уравнений и неравенств.
- •Построение графиков функций с помощью элементарных движений. Общая схема исследование функций с помощью производной.
- •Метод сечений при решении задач с параметром. Задачи, связанные с исследованием функций.
- •§10. Векторы, операции над ними. Скалярное, векторное и смешанное произведение. Проекции векторов. Примеры использования векторов в задачах физики.
- •§11. Уравнение прямой на плоскости в векторной форме.
- •Варианты контрольных работ
- •Дополнение 1 Вещественные числа
- •Сечения множества рациональных чисел
- •Перерізи множини раціональних чисел.
- •Сравнение сечений множества рациональных чисел
- •Порівняння перерізів множними раціональних чисел.
- •Теоремы об аппроксимации вещественных чисел рациональными
- •Теореми про апроксимацію дійсних чисел раціональними.
- •Теорема Дедекинда (непрерывность множества вещественных чисел)
- •Теорема Дедекінда (непрерівність множини дійсних чисел).
- •Сложение вещественных чисел
- •Додавання дійсних чисел
- •Произведение вещественных чисел
- •Дополнение 2 Исчисление высказываний
- •II. Правила построения формул ив.
- •III. Правила вывода ив
- •IV. Аксиомы ив.
- •V.Вывод
- •VI .Интерпретации
- •Математическая логика. Mathematical Logic Математична логіка
- •Формальный язык (аксиоматическая теория) и метаязык
- •Знаки, знакосочетания, алфавит.
- •Знаки, знакосполучення, алфавіт
- •Операции над словами
- •Операції над словами.
- •Выражения формального языка
- •Вирази формальної мови
- •Структурные знаки формального языка
- •Структурні знаки формальної мови
- •Переменные и константы (постоянные)
- •Зминні та сталі (константи)
- •Дополнение 3 Теорема про граничный переход в равенстве.
- •Дополнение 4 § теория пределов
- •Непрерывность и дифференцируемость
§. Теорема Абеля.
Поиски формул для решения уравнений пятой и более высоких степеней безуспешно продолжались до начала девятнадцатого века когда была, наконец, доказана следующая замечательная теорема
Т. Абеля: Общее алгебраическое уравнение с одним неизвестным степени выше четвертой не разрешимо в радикалах т.е. не существует формул, выражающих его корни через коэффициенты с помощью радикалов.
Более
того, для любой степени не меньшей пяти
можно указать уравнение с целыми
коэффициентами, корни которого никак
не выражаются через радикалы, сколь
угодно многоэтажные, если в подрадикальных
выражениях используются лишь целые и
рациональные числа. Таково, например,
уравнение
![]() .
Можно доказать, что это уравнение имеет
три вещественных и два комплексных
корня, но уравнение неразрешимо в
радикалах. Таким образом, запас чисел,
вещественных или комплексных, которые
служат корнями уравнений с целыми
коэффициентами ( такие числа называются
алгебраическими в противоположность
числам трансцендентным, которые не
являются корнями никаких уравнений с
целыми коэффициентами), много шире
запаса чисел, записываемых через
радикалы.
.
Можно доказать, что это уравнение имеет
три вещественных и два комплексных
корня, но уравнение неразрешимо в
радикалах. Таким образом, запас чисел,
вещественных или комплексных, которые
служат корнями уравнений с целыми
коэффициентами ( такие числа называются
алгебраическими в противоположность
числам трансцендентным, которые не
являются корнями никаких уравнений с
целыми коэффициентами), много шире
запаса чисел, записываемых через
радикалы.
Теория алгебраических чисел является важной ветвью алгебры. Доказательство невозможности разрешения в радикалах уравнений степени выше четвертой найдено Абелем (1802 – 1829). Существование не разрешимых в радикалах уравнений с целыми коэффициентами установил Галуа (1811 – 1832). Он также нашел условия, при которых уравнение может быть решено в радикалах. Все эти результаты потребовали создания новой глубокой теории, а именно теории групп. Понятие группы позволило исчерпать вопрос о разрешимости уравнений в радикалах, а позже оно нашло многочисленные применения в различных разделах математики и физики а также за их пределами и стало одним из важнейших объектов изучения в алгебре.
Отсутствие формул для решения уравнений степени выше четвертой не вызывает серьезных затруднений, если говорить о поиске корней таких уравнений. Оно полностью компенсируется многочисленными методами приближенного решения уравнений, которые даже для кубических уравнений ведут к цели гораздо быстрее, чем применение формул (там, где они вообще применимы) и последующее приближенное извлечение радикалов.
§. Еще о функциях комплексного переменного.
1.
Линейная функция
![]() ;
;
![]() .
.
Если
записать a в показательной
форме
![]() то:
то:
![]() – поворот на угол
– поворот на угол
![]() ,
,
![]() гомотетия с
коэффициентом k и
центром в начале координат,
гомотетия с
коэффициентом k и
центром в начале координат,
![]() – сдвиг плоскости на вектор b.
– сдвиг плоскости на вектор b.
Таким образом, линейная функция осуществляет поворот комплексной плоскости z с растяжением (сжатием) и последующим параллельным переносом. Линейная функция задает взаимно однозначное соответствие между комплексной плоскостью z и комплексной плоскостью w . При этом она преобразует прямые в прямые, сохраняя угол между ними и окружности в окружности, т.е. осуществляет конформное отображение комплексной плоскости z в комплексную плоскость w.
2.
Степенная функция
![]() ;
;
![]() .
.
Записав
z в показательной
форме:
![]()
![]() получим
получим
![]() .
.
При
этом окружности радиусом k
отображаются в окружности радиуса
![]() ,
а лучи исходящие из начала координат и
образующие угол
,
а лучи исходящие из начала координат и
образующие угол
![]() с осью абсцисс переходят в лучи из начала
координат и образующие угол
с осью абсцисс переходят в лучи из начала
координат и образующие угол
![]() с осью абсцисс.
с осью абсцисс.
Таким
образом: сектор
![]() в плоскости z
переходит во всю плоскость
в плоскости z
переходит во всю плоскость
![]() ,
сектор
,
сектор
![]() в плоскости z
также переходит во всю плоскость
в плоскости z
также переходит во всю плоскость
![]() и т.д. Следовательно, геометрический
образ плоскости z
при отображении
и т.д. Следовательно, геометрический
образ плоскости z
при отображении
![]() представляет собой плоскость
представляет собой плоскость
![]() ,
повторенную n раз.
,
повторенную n раз.
Из
сказанного выше следует, что отображение
не осуществляет взаимно однозначного
отображения между плоскостью z
и плоскостью
![]() .
Однако, если в качестве геометриче-ского
образа функции
.
Однако, если в качестве геометриче-ского
образа функции
![]() рассматривать более сложное многообразие,
чем обычную комплексную плоскость,
можно сохранить взаимную однозначность
отображения.
рассматривать более сложное многообразие,
чем обычную комплексную плоскость,
можно сохранить взаимную однозначность
отображения.
![]() ,
разрезанной по положительной части
действительной оси, на каждом из которых
,
разрезанной по положительной части
действительной оси, на каждом из которых
![]() изменяется в пределах
изменяется в пределах
![]() .
Сектору
.
Сектору
![]() плоскости z функция
плоскости z функция
![]() ставит в соответствие k-й
лист плоскости
ставит в соответствие k-й
лист плоскости
![]() ;
луч
;
луч
![]() переходит в верхний берег разреза k-го
листа, а луч
переходит в верхний берег разреза k-го
листа, а луч
![]() – в нижний берег разреза этого же k-го
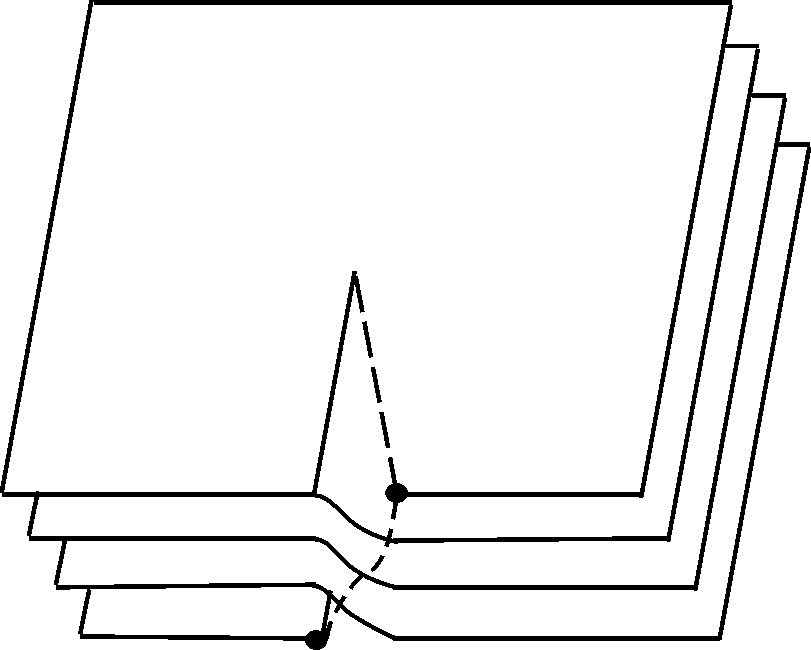
листа. Построим из этих листов непрерывное
геометрическое многообразие так, чтобы
непрерывному движению точки на плоскости
z соответствовало
непрерывное точки
– в нижний берег разреза этого же k-го
листа. Построим из этих листов непрерывное
геометрическое многообразие так, чтобы
непрерывному движению точки на плоскости
z соответствовало
непрерывное точки
![]() на данном многообразии (смотри рисунок).
Для этого заметим, что нижний берег
разреза k-го листа и
верхний берег разреза
на данном многообразии (смотри рисунок).
Для этого заметим, что нижний берег
разреза k-го листа и
верхний берег разреза
![]() -го
листа имеют один и тот же аргумент
-го
листа имеют один и тот же аргумент
![]() .
Когда точка z в
своем непрерывном движении по плоскости
z переходит из одного
сектора в другой, соответствующая ей
точка
.
Когда точка z в
своем непрерывном движении по плоскости
z переходит из одного
сектора в другой, соответствующая ей
точка
![]() переходит с одного листа плоскости
переходит с одного листа плоскости
![]() на следующий лист. Очевидно, чтобы
сохранить непрерывность отображения
мы должны соединить соседние листы,
склеивая нижний берег разреза k-го
листа с верхним берегом разреза
на следующий лист. Очевидно, чтобы
сохранить непрерывность отображения
мы должны соединить соседние листы,
склеивая нижний берег разреза k-го
листа с верхним берегом разреза
![]() -го
листа. При этом остаются свободными
верхний берег разреза 1-го листа и нижний
берег разреза
-го
листа. При этом остаются свободными
верхний берег разреза 1-го листа и нижний
берег разреза
![]() -го
листа. Пусть точка z
совершит на плоскости z
полный оборот вокруг точки
-го
листа. Пусть точка z
совершит на плоскости z
полный оборот вокруг точки
![]() ,
последовательно пройдя все
,
последовательно пройдя все
![]() секторов этой плоскости, начиная с
первого сектора, и вернется к своему
первоначальному положению. Тогда
соответствующая ей точка
секторов этой плоскости, начиная с
первого сектора, и вернется к своему
первоначальному положению. Тогда
соответствующая ей точка
![]() пройдет
пройдет
![]() листов и, чтобы она вернулась на первый
лист, надо склеить оставшиеся свободными
берега разрезов на 1-ом и
листов и, чтобы она вернулась на первый
лист, надо склеить оставшиеся свободными
берега разрезов на 1-ом и
![]() -ом
листах. Тем самым полной плоскости z
функция
-ом
листах. Тем самым полной плоскости z
функция
![]() ставит в соответствие
ставит в соответствие
![]() листов плоскости
листов плоскости
![]() ,
склеенных указанным выше способом.
Такое геометрическое многообразие
представляет собой
,
склеенных указанным выше способом.
Такое геометрическое многообразие
представляет собой
![]() -листную
риманову поверхность, а функция
-листную
риманову поверхность, а функция
![]() является
является
![]() -листной
функцией. Функция
-листной
функцией. Функция
![]() осуществляет взаимно однозначное
соответствие между комплексной плоскостью
z и
осуществляет взаимно однозначное
соответствие между комплексной плоскостью
z и
![]() -листной
римановой поверхностью.
-листной
римановой поверхностью.
3.
Корень натуральной степени
![]() .
.
![]() ;
;
![]() .
.
Функция
является многозначной и осуществляет
взаимно однозначное соответствие между
![]() -листной
римановой поверхностью и комплексной
плоскостью z. При этом
k-й лист римановой
поверхности переходит в сектор
-листной
римановой поверхностью и комплексной
плоскостью z. При этом
k-й лист римановой
поверхности переходит в сектор
![]() плоскости z.
плоскости z.
4.
Показательная функция (экспонента):
![]() ;
;
Основное
свойство показательной функции
![]() .
Тогда
.
Тогда
![]() .
.
Для
вещественных значений
![]() значения
значения
![]() показательной функции комплексного
аргумента совпадают со значением
вещественной показательной функции
вещественного аргумента.
показательной функции комплексного
аргумента совпадают со значением
вещественной показательной функции
вещественного аргумента.
Функция
![]() периодична с чисто мнимым периодом
периодична с чисто мнимым периодом
![]() :
:
![]() .
.
Тогда:
![]() .
.
Взаимная
однозначность отображения
![]() достигается, если ограничиться, скажем,
полосой
достигается, если ограничиться, скажем,
полосой
![]() .
.
Горизонтальная
прямая
![]() при отображении
при отображении
![]() переходит в луч
переходит в луч
![]() ,
в частности, действительная прямая
y=0 (как и всякая прямая
,
в частности, действительная прямая
y=0 (как и всякая прямая
![]() ) переходит в вещественную положительную
полупрямую
) переходит в вещественную положительную
полупрямую
![]() ,а
прямая
,а
прямая
![]() – в вещественную отрицательную
полупрямую. Значит, полоса
– в вещественную отрицательную
полупрямую. Значит, полоса
![]() в плоскости z переходит
во всю плоскость w.
Полоса
в плоскости z переходит
во всю плоскость w.
Полоса
![]() в плоскости z также
переходит во всю плоскость w.
в плоскости z также
переходит во всю плоскость w.
Отрезки
![]() (
(![]() )
отображаются на окружности
)
отображаются на окружности
![]() ,
в частности отрезок мнимой оси
,
в частности отрезок мнимой оси
![]()
![]() переходит в единичную окружность
переходит в единичную окружность
![]() .
.
Полуполоса
![]() ,
,![]() отображается на внешность единичного
круга
отображается на внешность единичного
круга
![]() .
.
Полуполоса
![]() ,
,![]() отображается на внутренность единичного
круга
отображается на внутренность единичного
круга
![]() .
.
Полоса
![]() отображается на верхнюю полуплоскость
отображается на верхнюю полуплоскость
![]() ,
полоса
,
полоса
![]() – на нижнюю полуплоскость.
– на нижнюю полуплоскость.
Из
выше сказанного заключаем, что
геометрический образ плоскости z
при отображении
![]() представляет собой плоскость
представляет собой плоскость
![]() ,
повторенную бесконечное число раз.
,
повторенную бесконечное число раз.
Тем
самым полной плоскости z
функция
![]() ставит в соответствие бесконечное число
листов плоскости
ставит в соответствие бесконечное число
листов плоскости
![]() ,
склеенных способом, аналогичным тому
который применялся для степенной
функции, за исключением того, что теперь
этих листом бесконечно много как снизу,
так и сверху.
,
склеенных способом, аналогичным тому
который применялся для степенной
функции, за исключением того, что теперь
этих листом бесконечно много как снизу,
так и сверху.
Такое
геометрическое многообразие представляет
собой бесконечно листную риманову
поверхность, а функция
![]() является бесконечно листной функцией.
Функция
является бесконечно листной функцией.
Функция
![]() осуществляет взаимно однозначное
соответствие между комплексной плоскостью
z и бесконечно листной
римановой поверхностью.
осуществляет взаимно однозначное
соответствие между комплексной плоскостью
z и бесконечно листной
римановой поверхностью.
5.
Логарифмическая функция:
![]() ;
;
Логарифмическая
функция является функцией обратной
показательной функцией и, поэтому,
является функцией многозначной:
![]() ;
;
![]() .
.
Она
осуществляет взаимно однозначное
соответствие между бесконечно листной
римановой поверхностью и плоскостью
w, при этом каждый лист
римановой поверхности переходит в
горизонтальную полосу
![]() .
.
