
- •ПРЕДИСЛОВИЕ
- •ЧАСТЬ I. ПРОСТРАНСТВА И КООРДИНАТЫ
- •Аффинные пространства
- •Аффинные евклидовы пространства
- •Аффинные координаты и преобразования
- •Криволинейные координаты
- •Криволинейные системы координат
- •Локальные базисы
- •ЧАСТЬ II. КИНЕМАТИКА
- •Кинематика точки
- •Коэффициенты Ламе. Проекции скорости точки на оси криволинейной системы координат
- •Проекции ускорения точки на оси ортогональной криволинейной системы координат
- •Описание движения точки в естественных координатах
- •Определение кривизны траектории точки по движению
- •Два примера движения точки
- •Кинематика твердого тела
- •Движение механической системы. Твердое тело. Число степеней свободы положения. Аффинное пространство и координаты, связанные с твердым телом
- •Группа движений аффинного евклидова пространства
- •Поступательное движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Плоское движение твердого тела
- •Движение твердого тела вокруг неподвижной точки
- •Угловая скорость, формула Эйлера и движение твердого тела в общем случае
- •Сложное движение
- •Сложное движение точки. Основные понятия
- •Относительная производная
- •Теорема сложения скоростей в сложном движении точки
- •Теорема сложения ускорений в сложном движении точки
- •Теорема о сложении угловых скоростей в сложном движении твердого тела
- •ЧАСТЬ III. ДИНАМИКА
- •Уравнения движения и основные законы динамики механической системы
- •Принцип детерминированности и уравнение Ньютона
- •Инерциальные системы координат
- •Сила и масса. Второй и третий законы Ньютона
- •Законы сил
- •Две задачи динамики
- •Уравнения движения механической системы
- •Теорема об изменении главного вектора количества движения
- •Уравнение движения центра инерции
- •Кинетический момент относительно неподвижной точки и теорема о его изменении
- •Движение точки в центральном поле сил
- •Изменение кинетического момента, вычисляемого относительно подвижного полюса
- •Работа силы и изменение кинетической энергии материальной точки
- •Условия потенциальности силового поля
- •Кинетическая энергия системы и теорема Кенига
- •Теорема об изменении кинетической энергии системы
- •Движение точки в центральном поле сил (продолжение)
- •Динамика твердого тела
- •Масса и плотность. Геометрия масс
- •Основные законы динамики твердого тела
- •Вращение твердого тела вокруг неподвижной точки
- •Уравнения движения свободного твердого тела
- •Динамика точки с переменной массой
- •Уравнение Мещерского
- •Две задачи Циолковского
- •ЧАСТЬ IV. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- •Общее уравнение механики
- •Cвязи, реакции. Обобщенные кооpдинаты
- •Изохронные ваpиации
- •Идеальные связи. Общее уравнение механики и принцип возможных перемещений
- •Общее уравнение механики в лагранжевых координатах
- •Уравнения Лагранжа
- •Уpавнения Лагpанжа II pода, их инваpиантность
- •Разрешимость уравнений Лагранжа II рода относительно старших производных
- •Обобщенный потенциал и уравнения Лагранжа II рода
- •Уравнения Лагранжа I рода и реакции идеальных связей
- •Канонические уравнения механики
- •Вывод канонических уравнений
- •Первые интегралы канонических уравнений
- •Метод Якоби решения канонических уравнений
- •Решение задачи о движении точки в центральном поле методом Якоби
- •Вариационные принципы механики
- •Дифференциальный принцип Даламбера-Лагранжа в декартовых переменных
- •Дифференциальный принцип Даламбера-Лагранжа в канонических переменных
- •Функционал и функция действия
- •Интегральный принцип наименьшего действия при изохронном варьировании (Принцип Гамильтона)
- •ЧАСТЬ V. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
- •Структуры и пространства
- •Группы, кольца, поля
- •Векторные пространства
- •Метрические пространства
- •Банаховы, гильбертовы и евклидовы пространства
- •Пространства Rn
- •Тензоры
- •Сопряженные пространства
- •Два определения тензора и их эквивалентность
- •Примеры тензоров
- •Алгебраические операции над тензорами
- •ЧАСТЬ VI. МАТЕРИАЛЫ ДЛЯ ЗАНЯТИЙ
- •Проверочные вопросы
- •Экзаменационные вопросы
- •Тесты
- •Упражнения
- •Литература
- •Предметный указатель
- •Оглавление

Перейти к оглавлению на странице: 256
Для рассматриваемой модели Земли в качестве криволинейных координат точки M часто рассматривают ее сферические координаты (r, ϕ, ϑ), называемые сферическим радиусом, долго-
той и широтой и задаваемые равенствами x = r sin ϑ cos ϕ, y =
r sin ϑ sin ϕ, z = r cos ϑ при r (0, +∞), ϕ [0, 2π), ϑ [−π2 , π2 ]. С этими координатами связаны и наиболее известные коорди-
наты географические. Для их введения конкретизируют направ-
~ ~ ~
ление ортов i, j, k , привязывая их не только к плоскости экватора, но еще к одной конкретной точке на реальной Земле лежащую на
~ |
|
экваторе точку O + R i выбирают так, что плоскость, проходящая |
|
~ |
~ |
через точки O, O + R k , O + R i, содержит и точку, совпадающую
со специальной отметкой у Гринвичской обсерватории возле Лондона. Координаты ϑ, ϕ −π, r −R называют тогда географическими широтой, долготой и высотой точки M .
С географическими координатами связаны такие общеизвестные понятия, как меридианы и параллели, северная и южная широты, восточная и западная долготы и их градусное измерение.
Упражнение 1.5. Введите понятия меридианов и параллелей, северной и южной широты, восточной и западной долготы, и их градусное измерение. Приведите также соответствующий рисунок.
§2. Группа движений аффинного евклидова пространства
Предварительные сведения
Здесь мы вспомним начальные сведения из теории групп.
Бинарной алгебраической операцией или законом композиции на множестве X называют отображение τ : X × X → X . Вместо τ(a, b) пишут aτb, например a b, a◦b, a+b, a·b (или ab). В последних двух случаях говорят соответственно о сумме и произведении элементов a и b, то есть законы композиции ” + ” и ” ·” называют суммой и произведением. Если ” ” закон композиции на X , то пару (X, ) называют алгебраической системой или алгебраической структурой. Чаще говорят просто об алгебраической системе X . Если ( a, b, c X) (a (b c) = (a b) c), то закон ” ” называется ассоциативным. Если закон композиции ” ” ассоциативен, то алгебраическую систему (X, ) называют полугруппой.
40
Перейти к оглавлению на странице: 256
Элемент e X называется единичным или нейтральным относительно закона композиции ” ”, если ( x X) (e x = x e = x). В алгебраической системе не может быть более одного единичного элемента. Полугруппу с единицей называют моноидом. Элемент a моноида (X, , e) называют обратимым, если ( b X) (a b = b a = e). Для элемента b такого, что a b = b a = e, используют обозначение a−1 . Моноид, все элементы которого обратимы называют группой. Закон композиции ” ” называется коммутативным, если ( a, b X) (a b = b a). Группу с коммутативным законом композиции называют абелевой (или коммутативной) группой.
Если (G, ) (или просто G) группа, e ее единица и выполнены условия H G, e H, (h1, h2 H) (h1 h2 H), (h H) (h−1 H), то ( H, |H) (или просто H ) называется подгруппой группы G.
Важнейшие для нас примеры групп группы преобразований. Пусть s(Ω) множество всех биективных отображений f : Ω → Ω. На этом множестве в качестве закона композиции можно задать суперпозицию отображений. Точнее говоря, в качестве закона композиции τ можно взять отображение τ : s(Ω)×s(Ω) → s(Ω) такое, что
( f, ϕ s(Ω)) (τ(f, ϕ) = f ◦ ϕ), где ( x Ω) ((f ◦ ϕ)(x) = f(ϕ(x))). Оказывается, что s(Ω) с таким законом композиции группа, причем ее единицей является тождественное отображение, то есть отображение idΩ : Ω → Ω такое, что ( x Ω) (idΩ(x) = x) .
Группа движений твердого тела
Вернемся к движению механической системы в E3 . Мы опре-
делили его как семейство DM = |
Dτ : J → E3 |
τ T дважды непре- |
|||||||||
рывно дифференцируемых |
функций, где каждая функция D |
|
|
||||||||
|
|
M |
|
|
системы |
|
τ |
||||
определяет движение одной точки |
τ механической |
M |
. |
||||||||
|
|
3 |
|
|
|||||||
Пусть (O,~e1,~e2,~e3) некоторый фиксированный репер в E |
|
(непо- |
|||||||||
движный репер) и пусть |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
Xj |
xjτ (t)~ej, τ T. |
|
|
|
|
|
|
|||
Dτ (t) = O + |
|
|
(2.1) |
||||||||
|
=1 |
|
|
|
|
|
|
|
|
|
|
Так как свободное твердое тело (т.е. твердое тело на классе всех движений в E3 ) имеет шесть степеней свободы, то функции xτj аргумента t J могут быть выражены через какие-то шесть
41
Перейти к оглавлению на странице: 256
скалярных функций q1(t), . . . , q6(t) (см. (1.3)). Мы сделаем это сейчас, и покажем тем самым еще раз, что свободное твердое тело имеет шесть степеней свободы положения.
Напомним, что под твердым телом мы понимаем подвижный экземпляр пространства или подвижный репер (см. §1). Четыре точки M0, M1, M2, M3 тела выберем так, чтобы векто-
M M |
, M M |
, M M |
образовывали ортонормированный базис |
||||
ры −−−−0 →1 |
−−−−0 →2 |
−−−−0 →3 |
|||||
~ ~ ~ |
|
|
3 |
|
|
|
|
(i1, i2, i3) пространства R |
. Для этого достаточно взять в качестве |
||||||
|
|||||||
|
|
|
|
|
|
~ |
|
M0 любую точку твердого тела и положить Mk = M0 + ik, k = |
|||||||
1, 2, 3. |
|
|
|
|
|
|
|
Каждая точка Mτ твердого тела определяется своими аффин- |
|||||||
|
|
|
|
~ |
~ |
~ |
|
ными координатами в репере (M0, i1 |
, i2 |
, i3): |
|||||
|
|
|
|
3 |
|
||
причем координаты yjτ
x3τ (t)
er3
O
x1τ (t)  er1
er1
Xj |
τ~ |
|
|
|
Mτ = M0 + |
yj ij, |
|
|
(2.2) |
=1 |
|
|
|
|
не зависят от времени t J . |
||||
ir3 = M 0 M3 |
|
|
|
|
Mτ |
|
|
|
|
y3τ |
r |
= |
M |
M2 |
|
i |
0 |
||
|
|
|||
|
2 |
|
|
|
M0 yτ2 y1τ
yτ2 y1τ 
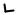 ir1 = M 0 M1 xτ2 (t) er2
ir1 = M 0 M1 xτ2 (t) er2 
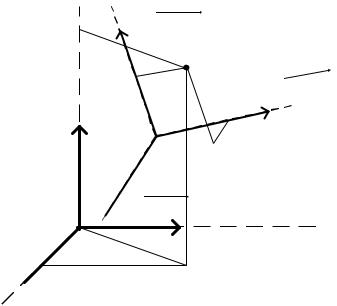
Рисунок 2.1
Формулы (2.1), (2.2) дают представление одной и той же точки Mτ в двух реперах неподвижном и подвижном (рис. 2.1). Векто-
~ ~ ~
ры i1, i2, i3 , построенные по движущимся точкам M0, M1, M2, M3 ,
42
Перейти к оглавлению на странице: 256
являются функциями времени:
~ ~
ij = ij(t), j = 1, 2, 3.
~ ~ ~
Ортонормированные базисы (~e1,~e2,~e3), (i1(t), i2(t), i3(t)) пространства R3 при любом t J связаны равенствами:
|
3 |
|
~ |
Xj |
|
ik = |
pk,j(t)~ej, k = 1, 2, 3, |
(2.3) |
|
=1 |
|
где матрица P = P (t) = (pk,j) ортогональна:
P −1 = P T , det P = ±1. |
(2.4) |
Будем считать, что det P = 1. Как мы знаем, в этом случае говорят, что базисы одинаково ориентированы. Если DM0 движение точки M0 и
3 |
|
Xj |
(2.5) |
DM0 (t) = O + aj(t)~ej, |
|
=1 |
|
то, в соответствии с формулами (2.10), (2.11) главы 1 получаем:
xj (t) = aj |
3 |
3 |
|
(2.6) |
Xk=1 pk,j(t) yk , j = 1, 2, 3, |
||||
τ |
(t) + |
|
τ |
|
|
|
|
|
|
yjτ = Xk=1 pj,k(xkτ − ak(t)), j = 1, 2, 3. |
(2.7) |
|||
Как известно, все элементы pk,j |
ортогональной матрицы P |
|||
могут быть выражены через три угла поворота (позже, при рассмотрении движения твердого тела вокруг неподвижной точки, мы выразим эти величины через так называемые углы Эйлера ϕ, ψ, θ). Если это сделано, то формулы (2.6) дают искомое представление для функций xτj через шесть функций времени a1, a2, a3, ϕ, ψ, θ.
|
Предположим теперь, что в момент t0 J |
подвижный репер |
||||||||||
|
~ |
~ |
~ |
|
|
|
|
|
|
|
|
|
(M0, i1, i2, i3) совпадает с неподвижным репером (O,~e1,~e2,~e3) и, |
||||||||||||
при каждом фиксированном t |
|
J , рассмотрим отображение D : |
||||||||||
E3 |
→ |
E3 |
|
|
|
(2.6) каждой точке M |
|
(t |
|
) = |
||
|
3 , сопоставляющее по формуле |
3 |
|
τ |
|
0 |
|
|||||
O + |
j=1 yjτ~ej точку Mτ (t) = O + |
j=1 xjτ~ej . Это отображение, |
||||||||||
очевидно, |
является биекцией |
E3 |
E3 |
|
|
|
|
|
||||
|
P |
|
|
на P . |
|
|
|
|
|
|||
43

Перейти к оглавлению на странице: 256
Подытожим полученное. Всякое движение твердого тела может быть задано через шесть скалярных функций a1, a2, a3, ϕ, ψ, θ по формулам (2.6), а значит всякому перемещению соответствует преобразование D : E3 → E3 , определяемое формулами (2.6). Задавая всевозможные движения (то есть задавая всевозможные функции a1, a2, a3, ϕ, ψ, θ) и фиксируя всевозможные моменты t J , мы будем получать те или иные перемещения твердого тела (за время от t0 до t) и соответствующие ему биекции D : E3 → E3 . Семейство D3 всех таких биекций оказывается подгруппой группы s(E3), ее называют группой движений в E3 (естественней было бы назвать ее группой перемещений в E3 ).
Упражнение 2.1. Докажите, что D3 является подгруппой
группы s(E3). Указание:
Свойства idE3 D3, (D1, D2 D3) (D1 ◦ D2 D3), (D D3) (D−1 D3) геометрически очевидны, если учесть, что тож-
дественное преобразование idE3 пространства E3 соответствует частному случаю перемещения тела такому, что начальное и конечное положения каждой его точки совпадают, композиция D1 ◦D2 соответствует двум последовательным перемещениям, а D−1 обратному перемещению из конечного положения в исходное.
Подгруппы движений
В механике изучают различные подгруппы группы D3 . Мы рассмотрим четыре из них. Вначале уточним обозначения. Символы xτj (t), Dτ (t), соответствующие точке Mτ , не все-
гда |
удобны и мы используем также очевидные обозначения |
|
xMτ (t), xM0 |
(t), DM0 (t), . . . (см. (2.5)). Символом M0(t) будем обо- |
|
j |
j |
|
значать образ точки M0 в ее движении, то есть величину DM0 (t) =
|
3 |
|
|
|
k |
|
0 k |
O + |
P |
xM0 |
|
|
|
||
|
~ej (см. (2.1)). Будем использовать также ранее вве- |
||||||
|
j=1 j |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
денные символы |
i (t) = M M |
||||||
|
|
−−−−→ для ортов ортонормированного ре- |
|||||
пера |
|
~ |
|
~ |
~ |
|
|
(M0(t), i1(t), i2 |
(t), i3(t)), жестко связанного с телом. Напом- |
||||||
~
ним, что орты ik(t), k = 1, 2, 3 связаны с неподвижными ортами ~ek, k = 1, 2, 3 равенствами (2.3), где P ортогональная матрица
~
(см. (2.4)), и M0(t0) = O, ik(t0) = ~ek, k = 1, 2, 3. Напомним также,
44

Перейти к оглавлению на странице: 256
что в формулах (2.5)–(2.7) величины xMj 0 (t) обозначались aj(t). Перейдем к обсуждению подгрупп движений.
~
Если орты ik(t), k = 1, 2, 3 не зависят от времени t J , то есть если матрица P (t) постоянна, то движение твердого тела называют поступательным (это определение, очевидно, эквивалентно тому, которое мы дали в конце §1). Так как P (t0) = E , то P (t) = E при всех t J , и из равенств (2.6) для поступательного движения получаем формулы:
xjτ (t) = aj(t) + yjτ , j = 1, 2, 3, τ T. |
(2.8) |
Из этих формул следует, что каждое поступательное движение твердого тела может быть задано тремя скалярными функциями. Каждому перемещению за время от t0 до t в этом движении по
τ |
τ |
τ |
→ |
E3 |
1 |
2 |
3 |
7−→ |
формуле (2.8) соответствует биекция D : E3 |
|
, (yτ |
, yτ |
, yτ ) |
D |
|||
(x1 (t), x2 (t), x3 (t)). Множеству всевозможных перемещений при всевозможных поступательных движениях твердого тела соответствует некоторое множество D13 таких биекций: будем говорить о нем как о множестве перемещений твердого тела, соответствующих преобразованиям вида (2.8).
Упражнение 2.2. Докажите, что множество D13 перемеще-
ний твердого тела, соответствующих преобразованиям вида (2.8), является абелевой подгруппой группы D3 .
Подгруппу D13 называют подгруппой сдвигов.
Если в пространстве, связанном с твердым телом, существует прямая l, все точки которой имеют неизменные координаты в репере (O,~e1,~e2,~e3) при t J , то такое движение твердого тела называют вращением вокруг неподвижной оси l.
Центр O репера (O,~e1,~e2,~e3) поместим в некоторую фиксированную точку оси l и орт ~e1 направим вдоль l. Символом ϕ = ϕ(t)
~
обозначим угол между ортами ~e2 и i2 .
Упражнение 2.3. Покажите, что при этих условиях и обозначениях формулы (2.6) можно записать в следующем ви-
де: |
|
|
|
|
|
|
|
|
|
|
|
|
|
xτ (t) |
|
|
|
1 |
0 |
0 |
|
yτ |
|
|
|
τ |
|
|
|
|
|
τ |
|
|||||
|
1 |
|
|
= |
|
0 |
cos ϕ(t) |
sin ϕ(t) |
|
1 |
|
. (2.9) |
|
xτ (t) |
|
yτ |
|||||||||
x3 |
(t) |
|
0 |
− sin ϕ(t) |
cos ϕ(t) |
y3 |
|
|||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
45

Перейти к оглавлению на странице: 256
По аналогии с множеством D13 введем в рассмотрение множество D23 перемещений твердого тела, соответствующих преобразованиям вида (2.9).
Упражнение 2.4. Докажите, что множество D23 перемеще-
ний твердого тела, соответствующих преобразованиям вида (2.9), является абелевой подгруппой группы D3 .
Подгруппу D23 называют подгруппой вращений вокруг оси. Пусть α плоскость в неподвижном пространстве. Симво-
лом Q(α, t0) обозначим сечение твердого тела плоскостью α в момент t0 J . Уточним, что Q(α, t0) это плоская фигура, состоящая из точек твердого тела, имеющих неизменные координаты в подвижной системе координат. Плоским или плоско-параллельным движением твердого тела называют его движение, при котором в неподвижном пространстве существует плоскость α такая, что сечение Q(α, t) принадлежит α при всех t J . Плоскость α называют плоскостью параллелизма. Если начало O неподвижного репера (O,~e1,~e2,~e3) вместе с ортами ~e1,~e2 поместить в плоскость α, то формулы (2.6) можно записать в следующем виде:
|
x1τ (t) |
|
|
a1(t) |
|
|
|
p1,1 |
τ |
|
|
|
|
||||
|
x2τ (t) |
|
= |
a2(t) |
|
+ |
|
p2,1 |
x3 (t) |
|
a3(t) |
|
0 |
||||
p1,2 |
0 |
|
y1τ |
|
|
|
0 |
τ |
. (2.10) |
||
p2,2 |
|
y2τ |
|
||
0 |
1 |
y3 |
|
||
Множество D33 перемещений твердого тела, соответствующих преобразованиям (2.10), подгруппа группы D3 , так как она изоморфна группе D2 .
Если в твердом теле существует точка C , координаты которой неизменны в неподвижном репере (O,~e1,~e2,~e3) при t J , то такое движение твердого тела называют вращением вокруг неподвижной точки C (это определение, очевидно, эквивалентно тому, которое мы дали в конце §1). Если начало O репера (O,~e1,~e2,~e3) поместить
в точку C , то формула (2.6) запишется в виде: |
|
|||||||
|
xτ (t) |
|
|
|
yτ |
|
|
|
τ |
|
τ |
|
|
||||
|
1 |
|
= P (t) |
|
1 |
|
|
(2.11) |
|
xτ (t) |
|
yτ |
. |
||||
x3 (t) |
|
y3 |
|
|
||||
|
2 |
|
|
|
2 |
|
|
|
Упражнение 2.5. Докажите, что множество D43 перемеще-
46
