Перейти к оглавлению на странице: 256

ГЛАВА 4. КИНЕМАТИКА ТВЕРДОГО ТЕЛА

Модель твердого тела и его движения важна в механике уже потому, что с ними тесно связано понятие аффинной (декартовой) системы координат, а без этого понятия мало что осталось бы от классической механики и ряда других, опирающихся на ее положения, разделов естествознания.

В§1 основные понятия, рассмотренные в предыдущей главе в рамках модели кинематики точки, обобщаются на случай механической системы из конечного или бесконечного множества точек, вводится модель твердого тела, понятие числа степеней свободы положения механической системы и обсуждается вопрос о связи понятий твердого тела, аффинного пространства, аффинных и криволинейных систем координат.

В§2 устанавливается взаимно-однозначное соответствие между множеством движений твердого тела и множеством преобразований движения аффинного евклидова пространства, наделенным структурой группы. Это позволяет рассмотреть различные классы движений твердого тела, соответствующие тем или иным подгруппам этой группы. В следующих параграфах главы изучается движение твердого тела для каждой из подгрупп. Общий случай движения твердого тела рассматривается в §7.

§1. Движение механической системы. Твердое тело. Число степеней свободы положения. Аффинное пространство и координаты, связанные с твердым телом

Движение механической системы

Символом T обозначим некоторое множество, далее это будет множество индексов τ , которыми помечены все точки механической системы. Символом J обозначим промежуток на прямой Rдалее это будет промежуток времени t, на котором определено движение механической системы.

Как и в модели кинематики точки, пространством будем считать аффинное евклидово пространство En, n = 1, 2, 3; точку этого пространства будем представлять радиус–вектором ~r в декартовой

~ ~ ~

системе координат и если, например n = 3, а i, j, k орты системы

34

Перейти к оглавлению на странице: 256

Механической системой в момент t0 или положением системы в момент t0 будем называть семейство M = {Mτ }τ T точек в En, n = 1, 2, 3. Движением этой системы будем называть семейство DM = {Dτ : J → En}τ T дважды непрерывно дифференцируемых функций времени t такое, что

Твердое тело

Различные множества движений DM назовем классами движений. Неизменяемой на классе движений назовем такую механическую систему, что

для любого движения этого класса. Механическую систему назовем сплошной связной средой на классе движений, если каждое ее положение есть область (то есть, открытое связное множество) или замкнутая область в En . Твердым телом или абсолютно твердым телом на классе движений назовем сплошную связную неизменяемую механическую систему на этом классе движений.

35

Перейти к оглавлению на странице: 256

Говорят, что механическая система имеет s степеней свободы положения на классе движений, если всякое движение этого класса может быть выражено через некоторую систему скалярных функций qi : J → R, i = 1, . . . , s и если хотя бы одно движение этого класса не может быть выражено ни через какую систему из меньшего числа скалярных функций. Если класс движений очевиден из контекста, то говорят просто о числе s степеней свободы механической системы. Понятие числа степеней свободы вначале обсудим на примере движений механической системы, состоящей из конечного числа N точек. Такая система на классе всех движений в En, n = 1, 2, 3 имеет очевидно s = n · N степеней свободы.

Рассмотрим такой подкласс всех движений этой системы, для которых координаты (xν, yν, zν), ν = 1, . . . , N ее точек удовлетворяют уравнениям

причем функции fν аргументов (x1, y1, z1, . . . , xN , yN , zN ) независимы при t J (будем считать, что ранг матрицы Якоби этих функций равен m). В этом случае говорят, что рассматривается механическая система из N точек, стесненная m голономными связями. Эти и другие виды связей мы обсудим еще при изучении аналитической динамики.

Упражнение 1.1. Механическая система в En , n = 1, 2, 3 из

N точек, стесненная m голономными связями имеет s = n · N − m степеней свободы.

Приведем два примера такой системы.

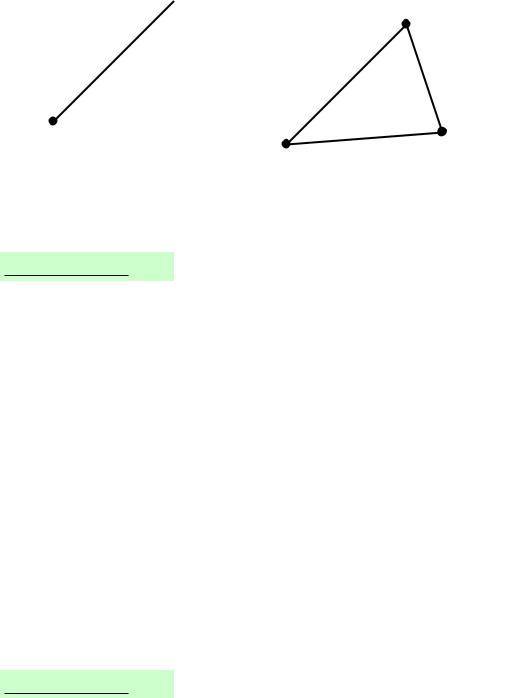
1. Движению отрезка длиной l в плоскости можно сопоставить механическую систему в E2 , состоящую из двух концевых точек отрезка M1 (x1, y1), M2 (x2, y2) и стесненную одной голономной

связью:

f = (x1 − x2)2 + (y1 − y2)2 − l2 = 0.

Здесь n = 2, N = 2, m = 1, поэтому s = 2 · 2 − 1 = 3 .

2. Движению треугольника в пространстве сопоставим систему в E3 , состоящую из точек M1 (x1, y1, z1), M2 (x2, y2, z2), M3 (x3, y3, z3) (вершин треугольника) и стесненную тремя голономными связями:

f1 = (x1 − x2)2 + (y1 − y2)2 + (z1 − z2)2 − l1,22 = 0,

36

Перейти к оглавлению на странице: 256

f2 = (x1 − x3)2 + (y1 − y3)2 + (z1 − z3)2 − l1,32 = 0, f2 = (x2 − x3)2 + (y2 − y3)2 + (z2 − z3)2 − l2,32 = 0,

где l1,2, l1,3, l2,3 длины сторон треугольника. Здесь n = 3, N = 3, m = 3, s = 3 · 3 − 3 = 6.

M 2 (x2 , y2 ) M 2 (x2 , y2 , z2 )

Упражнение 1.2. Приведите еще несколько подобных примеров.

Вернемся к случаю твердого тела. С твердым телом можно связать ортонормированный репер. Для этого достаточно задать в теле n + 1 независимые точки (почему это можно сделать?). Во все время движения (то есть при всех t J ) все точки тела будут иметь неизменяемые (то есть не зависящие от t J ) координаты в этом репере. Поэтому для этого частного случая механической системы, твердого тела, используют следующее удобное соглашение: твердое тело отождествляют с упомянутым выше репером (подвижным репером) или с экземпляром пространства, определяемым этим репером (подвижным пространством). Исходные репер и пространство называют при этом неподвижным репером и неподвижным пространством соответственно. Можно показать, что для твердого тела на классе всех его движений в En, n = 1, 2, 3 число степеней свободы положения равно:

Упражнение 1.3. Докажите равенство (1.5), пользуясь тем, что положение твердого тела можно задать координатами

37

Перейти к оглавлению на странице: 256

n + 1 его независимых точек, и формулой s = n · N − m для механической системы, состоящей из N точек и стесненной m голономными связями.

Теперь обсудим число степеней свободы твердого тела на двух важных классах его движений в E3 . Движение твердого тела называют поступательным, если любые два положения в этом движе-

течением времени может изменяться только начало репера. Дви-

го тела.

Упражнение 1.4. Найдите число степеней свободы положения твердого тела на этих двух классах движений.

Об используемых моделях пространства, времени и движения. Аффинное пространство и координаты, связанные с твердым телом

Когда в настоящем курсе классической механики мы говорим о движении механической системы и, в частности, твердого тела, то предполагаем, что речь идет о движении в каком-то аффинном евклидовом пространстве, и что нам известен хотя бы один ортонормированный репер, относительно которого можно рассматривать это движение. Если это предположение выполнено, то несложно построить другие реперы и другие аффинные пространства, но это не избавит нас как от самого предположения, так и от вопроса откуда берутся или, точнее, что означают с практической точки зрения исходное аффинное пространство и его репер? Здесь мы обсудим этот вопрос.

Мы придерживаемся той точки зрения, что исходные аффинное пространство и репер это математические модели чего-то "реального", а конкретнее, считаем, что исходное аффинное пространство математическая модель окружающего нас "реального" пространства, а исходный репер (или декартова система коор-

38

Перейти к оглавлению на странице: 256

динат) некоторая математическая конструкция, связанная с "реальным" твердым телом. Введя понятие движения механической системы мы представили его при помощи вектор-функций аргумента, который назвали временем. Естественно считать, что это времяматематическая модель "реального" времени. Твердым телом или абсолютно твердым телом (на классе движений) мы назвали сплошную связную неизменяемую механическую систему (на этом классе движений).

Таким образом, мы предполагаем, что относительно "реальных"пространства, времени, тел и их движения имеем достаточное интуитивное представление, чтобы строить те или иные модели классической механики. Выбор моделей определяется не только самими этими представлениями, но и, в частности, соображениями удобства. В этой связи напомним, что выше, помимо только что упомянутого определения твердого тела, мы договорились, ради удобства, отождествлять твердое тело с репером (подвижным репером) или с экземпляром пространства, определяемым этим репером (подвижным пространством). Тем самым мы ввели еще один вариант модели твердого тела, эквивалентный первому. С другой стороны, сама формулировка последней модели содержит в себе ответ на вопрос, который мы здесь обсуждали: как оказалось, в качестве "исходных" аффинного пространства и репера можно взять модель любого "реального" твердого тела. Эту модель твердого тела обычно называют "телом отсчета" или "системой отсчета" (при фиксированных единицах измерения длины и времени). В качестве примера "тела отсчета" рассмотрим простейшую, шаровую, модель Земли.

С моделью Земли в виде шара радиуса R свяжем ортонорми-

~r = (x, y, z) = x i+y j +z k в репере (O, i, j, k) (или, что фактически

то же, в декартовой системе координат Oxyz ) и, в то же время, это же множество радиус-векторов будем рассматривать как соответствующее векторное евклидово пространство R3 этого аффинного пространства.

39