Перейти к оглавлению на странице: 256

откуда выводим, что

и, так как при t → 0 истинны предельные соотношения

то из (3.13) при t → 0 получаем (3.11). Что и требовалось.

Теорема 3.1.

Доказательство.

Из формул (3.5), (3.11), (3.10) получаем

Что и требовалось.

§4. Определение кривизны траектории точки по движению

Согласно определению, данному в предыдущем пункте, кривизна траектории в точке, имеющей естественную координату s, (см. (3.10)) зависит только от этой координаты и не зависит от выбора параметризации этой траектории. Тем не менее, один из удобных методов нахождения кривизны, кинематический метод, использует параметризацию траектории задание движения точки по траектории как функции времени в декартовых или криволинейных координатах.

Кинематический метод

Пусть движение точки задано тройкой скалярных функций x(t), y(t), z(t). Пусть v = v(t), w = w(t) модули ее скорости и

29

Перейти к оглавлению на странице: 256

ускорения. Используя результаты предыдущего параграфа, выписываем следующую цепочку формул для вычисления K, %:

p

v = (x˙ (t))2 + (y˙(t))2 + (z˙(t))2,

Пусть теперь движение точки задано тройкой криволинейных координат скалярных функций q1(t), q2(t), q3(t), а v = v(t), w = w(t) попрежнему модули ее скорости и ускорения. В предположении, что эта система координат ортогональна, и используя формулы (1.5), (2.2) для проекций скорости и ускорения точки, получаем:

p

v = (vq1 (t))2 + (vq2 (t))2 + (vq3 (t))2,

(4.5)

p

w = (wq1 (t))2 + (wq2 (t))2 + (wq3 (t))2,

теперь по формулам (4.2), (4.3) можно вычислить величины K, %.

§5. Два примера движения точки

Мы рассмотрим примеры, которые позволят сопоставить известные со школы факты с введенными выше понятиями.

Прямолинейное движение

Так называют движение точки, траектория которой лежит на прямой. Начало системы Oxyz поместим на этой прямой, а ось x направим вдоль нее. Тогда получим уравнение траектории:

и, как следствие, формулы:

v2 = (x˙ (t))2 + (y˙(t))2 + (z˙(t))2 = (x˙ (t))2,

(5.2)

w2 = (¨x(t))2 + (¨y(t))2 + (¨z(t))2 = (¨x(t))2,

30

v(t) = α, где α постоянная. Так как v(t) = x˙ (t), то x(t) = αt+ β , где β произвольная постоянная. Если x(t0) = x0 , то x(t) = x0 + α(t −t0). Если ввести естественную координату s = |x −x0|, то s = |α(t−t0)|. Прямолинейное движение равнопеременное при w(t) = α, и постоянном α. Из w(t) = x¨(t) следует x(t) = αt2/2 + βt + γ , где β, γ произвольные постоянные. Если x(t0) = x0, x˙ (t0) = x˙ 0 , то

получаем формулу x(t) = x0 + x˙ 0(t − t0) + α(t − t0)2/2. Если ввести естественную координату s = |x−x0|, то s = |x˙ 0(t−t0)+α(t−t0)2/2|.

Движение по окружности

Здесь и далее будут использоваться понятия угла и угла поворота.

Опонятии угла и угла поворота:

(а)Углом поворота между векторами называется вектор

~

(б) Углом между векторами ~a и b, или углом между прямыми, проходящими через эти векторы (он равен наименьшему из углов

или наоборот, то имеют в виду угол поворота (~a, b) или (b,~a).

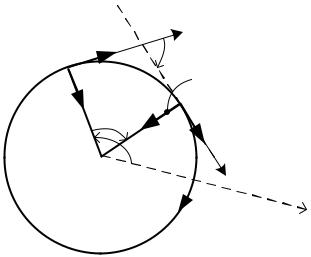
Движением по окружности называют любое движение точки, траектория которого лежит на окружности. Радиус кривизны, а значит и кривизну окружности радиуса R просто найти, опираясь на определение кривизны через угол смежности.

Пусть s приращение естественной координаты за время движения точки от момента t до момента t + t, а ϕ угол смежности за это время.

31

Перейти к оглавлению на странице: 2561

Рисунок 5.1

Так как s = R ϕ, то устремляя t к нулю (а тогда и

s, ϕ стремятся к нулю), получаем равенства: K = dϕ/ds =

lim (Δϕ/ s) = R−1 , % = R.

s→0

Сдвижением по окружности связывают векторные величины

угловую скорость и угловое ускорение, которые мы сейчас введем. Движение считаем заданным в цилиндрической системе координат (r, ϕ, z) равенствами:

Здесь полюс системы координат помещен в центр окружности, z = 0 уравнение плоскости, в которой лежит окружность, а ϕ полярный угол, отсчитываемый от фиксированного луча, исходящего из полюса и лежащего в этой плоскости. Приращение

32

Перейти к оглавлению на странице: 256

Пусть ~e единичный вектор, параллельный бинормали и исходящий из полюса центра окружности. Введем в рассмотрение следующие величины:

ϕ~e вектор угла поворота,

ω~cp = ϕt ~e средняя угловая скорость, ω~ = ϕ~˙e угловая скорость,

Движение по окружности называют равномерным вращением, если ω = ω0 , где ω0 постоянная (не зависит от времени). Так как ω = ϕ˙ , то

Движение по окружности называют равнопеременным вращением, если ε = ε0 , где ε0 постоянная.

Так как ε = ω˙ = ϕ¨, то

Упражнение 5.1. Движение точки задано в цилиндрических координатах:

где a, b, c положительные постоянные. Найти уравнение траектории этой точки. Найти скорость и ускорение точки и радиус кривизны траектории как функции аргумента r. Определить зависимость радиуса кривизны от естественной координаты.

33