Перейти к оглавлению на странице: 256

ний твердого тела, соответствующих преобразованиям вида (2.11), является абелевой подгруппой группы D3 .

D43 называют подгруппой вращений вокруг неподвижной точки C .

§3. Поступательное движение твердого тела

Закрепленные и свободные векторы

Напомним понятие закрепленного вектора (см. §1 главы 1). Если A точка аффинного пространства En , а ~a вектор связанного с ним векторного пространства Rn , то пару (A,~a) называют вектором ~a, закрепленным в точке A (или приложенным к точке A). Каждому закрепленному вектору (A,~a) соответствует

упорядоченная пара точек (A, A+~a), и каждой упорядоченной паре

−−→

точек (A, B) соответствует закрепленный вектор (A, AB). Поэтому закрепленным вектором называют также упорядоченную пару

точек аффинного пространства. Вместо того, чтобы говорить о за-

−−→

крепленном векторе (A, AB), будем также говорить о закреплен-

−−→ −−→

ном векторе AB или (A, B). Заметим однако, что обозначение AB

−−→

для закрепленного вектора (A, AB) может привести к недоразуме-

−−→

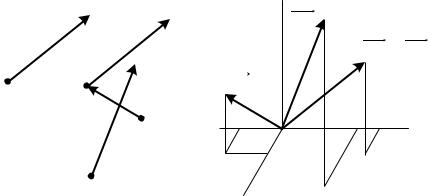
нию см., например, равенство (3.1). Закрепленный вектор AB обычно изображают на рисунке стрелкой от A к B и называют направленным отрезком. В противоположность названию закрепленный вектор, для векторов из Rn используют название свободный вектор. Отличие закрепленных векторов от свободных иллюстрирует рис. 3.1.

Поступательное движение твердого тела

Движение твердого тела называют поступательным, если

−−−−−−−→ −−−−−−−→

( t1, t2 J) A(t1)B(t1) = A(t2)B(t2) (3.1)

для любой пары произвольно выбранных несовпадающих точек A, B этого тела (пространства, связанного с телом). Иначе говоря, движение твердого тела называют поступательным, если направленный отрезок, соединяющий любые две несовпадающие точки этого тела, перемещается параллельно самому себе во все время

47

Перейти к оглавлению на странице: 256

Рисунок 3.1

движения. Это второе определение поступательного движения твердого тела, первое мы дали в §2. Докажем их эквивалентность.

yjA, yjB, j = 1, 2, 3 координаты точек A и B в подвижном репере, то

зависит от t J . В силу произвольности выбора точек A и B , это

48

Перейти к оглавлению на странице: 256

означает, что движение твердого тела является поступательным и в смысле второго определения.

б) Если движение тела является поступательным в смысле второ-

~

го определения, то, в частности, каждый из трех векторов ij(t) =

−−−−−−−−→

M0(t)Mj(t), j = 1, 2, 3 является постоянным при t J , то есть движение поступательно и в смысле первого определения.

Теорема 3.1. Поступательное движение твердого тела обладает следующими свойствами:

α) положение тела определяется положением любой его точки;

β) перемещения всех точек тела за время от t0 до t1 равны между собой; γ) скорости всех точек тела равны между собой;

δ) ускорения всех точек тела равны между собой; ε) твердое тело на классе поступательных движений имеет три степени свободы.

Доказательство.

α)Прежде всего отметим, что для того, чтобы идентифицировать точки тела, достаточно задать их координаты в подвижном репере. Положение твердого тела в момент t в неподвижном репере задается семейством {(xτ1 (t), xτ2 (t), xτ3 (t))}τ T . Если задано положение (xA1 (t), xA2 (t), xA3 (t)) одной его точки A, имеющей в подвижном репере координаты (y1A, y2A, y3A), то используя равенства (2.8) для координат точки A, получаем:

Подставляя выражения aj(t) в формулу (2.8), находим для любой точки тела искомое выражение ее координат xτj (t) через известные ее координаты yjτ в подвижном репере и известные координаты xAj (t) и yjA точки A:

β, γ, δ) Согласно определению, движение, скорость и ускорение точки Mτ , имеющей координаты xτ1 (t), xτ2 (t), xτ3 (t) в репере

(O,~e1,~e2,~e3), это вектор-функции ~r τ (t) = (xτ1 (t), xτ2 (t), xτ3 (t)),

49

(3.6) получаем (при очевидных обозначениях):

~r τ (t1)−~r τ (t) = ~r A(t1)−~r A(t), ~v τ (t) = ~v A(t), w~ τ (t) = w~ A(t), (3.7)

откуда и следуют свойства β, γ, δ .

Доказанные свойства геометрически очевидны, см. рис. 3.2.

§4. Вращение твердого тела вокруг неподвижной оси

В §2 вращением вокруг неподвижной оси мы назвали такое движение твердого тела, для которого в пространстве, связанном с этим телом, существует прямая (ось вращения), все точки которой имеют неизменные координаты в неподвижном репере. Пусть O, O1 две различные точки оси вращения. В качестве

50

Перейти к оглавлению на странице: 256

вить себе как тройку приложенных к точке O единичных взаимно ортогональных и жестко связанных с телом векторов, первый из

ток времени, на котором рассматривается движение.

Как мы установили в §2, в этом случае вращению твердого тела вокруг оси соответствуют преобразования координат по формулам (2.9). Если точка M тела имеет координаты y1, y2, y3 и x1(t), x2(t), x3(t) в подвижном и неподвижном реперах соответственно, то из этих формул можно получить равенство x22(t) + x23(t) = y22 +y32 . Это означает, что траектория любой точки твердого тела при его вращении вокруг неподвижной оси есть окружность с центром на оси вращения, что геометрически очевидно (рис. 4.1).

В §5 главы 3 мы рассмотрели движение точки по окружности. Эти результаты можно использовать и здесь для нахождения

51

Перейти к оглавлению на странице: 256

скоростей и ускорений точек твердого тела.

Пусть A точка пересечения оси вращения с плоскостью,

Теорема 4.1. В принятых обозначениях истинны формулы:

Доказательство. Вторая из формул следует из первой, которую

A

Рисунок 4.2

Заметим, что угловая скорость ω~ не зависит от выбора точки твердого тела, поэтому она называется угловой скоростью твердого

52