
- •ПРЕДИСЛОВИЕ
- •ЧАСТЬ I. ПРОСТРАНСТВА И КООРДИНАТЫ
- •Аффинные пространства
- •Аффинные евклидовы пространства
- •Аффинные координаты и преобразования
- •Криволинейные координаты
- •Криволинейные системы координат
- •Локальные базисы
- •ЧАСТЬ II. КИНЕМАТИКА
- •Кинематика точки
- •Коэффициенты Ламе. Проекции скорости точки на оси криволинейной системы координат
- •Проекции ускорения точки на оси ортогональной криволинейной системы координат
- •Описание движения точки в естественных координатах
- •Определение кривизны траектории точки по движению
- •Два примера движения точки
- •Кинематика твердого тела
- •Движение механической системы. Твердое тело. Число степеней свободы положения. Аффинное пространство и координаты, связанные с твердым телом
- •Группа движений аффинного евклидова пространства
- •Поступательное движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Плоское движение твердого тела
- •Движение твердого тела вокруг неподвижной точки
- •Угловая скорость, формула Эйлера и движение твердого тела в общем случае
- •Сложное движение
- •Сложное движение точки. Основные понятия
- •Относительная производная
- •Теорема сложения скоростей в сложном движении точки
- •Теорема сложения ускорений в сложном движении точки
- •Теорема о сложении угловых скоростей в сложном движении твердого тела
- •ЧАСТЬ III. ДИНАМИКА
- •Уравнения движения и основные законы динамики механической системы
- •Принцип детерминированности и уравнение Ньютона
- •Инерциальные системы координат
- •Сила и масса. Второй и третий законы Ньютона
- •Законы сил
- •Две задачи динамики
- •Уравнения движения механической системы
- •Теорема об изменении главного вектора количества движения
- •Уравнение движения центра инерции
- •Кинетический момент относительно неподвижной точки и теорема о его изменении
- •Движение точки в центральном поле сил
- •Изменение кинетического момента, вычисляемого относительно подвижного полюса
- •Работа силы и изменение кинетической энергии материальной точки
- •Условия потенциальности силового поля
- •Кинетическая энергия системы и теорема Кенига
- •Теорема об изменении кинетической энергии системы
- •Движение точки в центральном поле сил (продолжение)
- •Динамика твердого тела
- •Масса и плотность. Геометрия масс
- •Основные законы динамики твердого тела
- •Вращение твердого тела вокруг неподвижной точки
- •Уравнения движения свободного твердого тела
- •Динамика точки с переменной массой
- •Уравнение Мещерского
- •Две задачи Циолковского
- •ЧАСТЬ IV. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- •Общее уравнение механики
- •Cвязи, реакции. Обобщенные кооpдинаты
- •Изохронные ваpиации
- •Идеальные связи. Общее уравнение механики и принцип возможных перемещений
- •Общее уравнение механики в лагранжевых координатах
- •Уравнения Лагранжа
- •Уpавнения Лагpанжа II pода, их инваpиантность
- •Разрешимость уравнений Лагранжа II рода относительно старших производных
- •Обобщенный потенциал и уравнения Лагранжа II рода
- •Уравнения Лагранжа I рода и реакции идеальных связей
- •Канонические уравнения механики
- •Вывод канонических уравнений
- •Первые интегралы канонических уравнений
- •Метод Якоби решения канонических уравнений
- •Решение задачи о движении точки в центральном поле методом Якоби
- •Вариационные принципы механики
- •Дифференциальный принцип Даламбера-Лагранжа в декартовых переменных
- •Дифференциальный принцип Даламбера-Лагранжа в канонических переменных
- •Функционал и функция действия
- •Интегральный принцип наименьшего действия при изохронном варьировании (Принцип Гамильтона)
- •ЧАСТЬ V. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
- •Структуры и пространства
- •Группы, кольца, поля
- •Векторные пространства
- •Метрические пространства
- •Банаховы, гильбертовы и евклидовы пространства
- •Пространства Rn
- •Тензоры
- •Сопряженные пространства
- •Два определения тензора и их эквивалентность
- •Примеры тензоров
- •Алгебраические операции над тензорами
- •ЧАСТЬ VI. МАТЕРИАЛЫ ДЛЯ ЗАНЯТИЙ
- •Проверочные вопросы
- •Экзаменационные вопросы
- •Тесты
- •Упражнения
- •Литература
- •Предметный указатель
- •Оглавление

Перейти к оглавлению на странице: 256
Пример 2.1. Рассмотрим цилиндрическую систему коор-
динат. Так как она ортогональна, то получаем:
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
v = q(%˙)2 + (%ϕ˙)2 |
+ (z˙)2, T = |
(%˙)2 + (%ϕ˙)2 + (z˙)2 |
, |
(2.11) |
||||||||||||||||
2 |
||||||||||||||||||||
∂T |
= %ϕ˙2, |
∂T |
= %,˙ |
∂T |
= 0, |
∂T |
= %2ϕ,˙ |
∂T |
= 0, |
∂T |
= z˙ |
(2.12) |
||||||||
∂% |
∂%˙ |
|
∂ϕ |
|
∂ϕ˙ |
∂z |
|
∂z˙ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
и из формулы (2.2) получаем следующие выражения для проекций ускорения на оси цилиндрической системы координат:
w% = %¨ − %ϕ˙2, wϕ = 2%˙ϕ˙ + %ϕ,¨ wz = z¨. |
(2.13) |
Упражнение 2.1. Найти выражения для скорости и ускоре-
ния точки в обобщенных сферических координатах u, v, w, задаваемых формулами:
x = au cos v sin w, y = bu sin v sin w, z = cu cos w |
(2.14) |
при
0 6 u < ∞, 0 6 v < 2π, 0 6 w < π, a, b, c, > 0, a 6= b. (2.15)
§3. Описание движения точки в естественных координатах
В отличие от криволинейных координат, которые определяются в каких-то областях D Rn при n = 1, 2, 3, естественная система координат определяется на траектории движения точки. В этих координатах скорость и ускорение точки имеют понятную геометрическую интерпретацию и простые формулы для соответствующих проекций на оси координат.
Будем предполагать, что траектория движения точки задана параметрически вектор-функцией ~r(t) = (x(t), y(t), z(t)) на некотором промежутке J R времени t.
24
Перейти к оглавлению на1 странице: 256
нормальная плоскость  спрямляющая плоскость
спрямляющая плоскость
A |
r |
r |
|
|
b |
n |
V2 |
|
|
|
|
|
|
|
|
M1 |
|
V |
M2 |
|
|
|
||
|
|
|
|
|
r |
|
τr |
r |
|
(a) |
|
V1 |
|
|
r |
|
rr(t) |
|
|
|
|
|
|
rr(b) |
|
|
|
|
rr(t + |
соприкасающаяся плоскость
B
t)
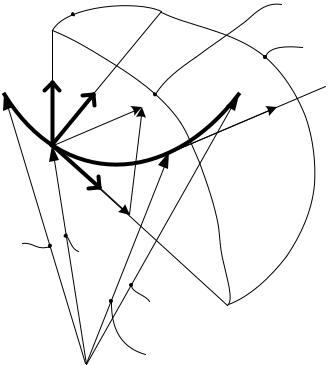
Рисунок 3.1
Пусть a, b J, a < b, а A = (x(a), y(a), z(a)) , B = (x(b), y(b), z(b)) начало и конец участка траектории AB , соответствующего движению точки (рис. 3.1). Будем предполагать, что на этом участке (то есть при t [a, b] ) функция ~r(t) непрерывно дифференцируема k раз (обычно предполагают, что k = 2), причем выполнено условие
d~r |
~ |
|
|
6= 0, t [a, b]. |
(3.1) |
dt |
Как известно, при сделанных предположениях, в каждой точке ~r(t) участка AB (который мы будем далее называть регулярным участком траектории) траектория имеет касательную, совпадающую по направлению с вектором скорости ~v = ~r˙(t). Пусть a < t < t + t < b и используются обозначения:
M1 = (x(t), y(t), z(t)) , M2 = (x(t + t), y(t + t), z(t + t)) ,
25

|
Перейти к оглавлению на странице: 256 |
|
˙ |
˙ |
− ~v1. |
~v1 = ~r(t), ~v2 |
= ~r(t + t), ~v = ~v2 |
|
Упражнение 3.1. Пусть выполнено условие:
_
(а) никакая часть дуги AB не является прямолинейной. Показать, что в этом случае плоскость Π(M1,~v1, ~v), проходящая через точку M1 и параллельная векторам ~v1,~v2 , имеет предельное положение при t → 0, то есть имеет предел при ~v → 0 единичный вектор нормали, определяющий направление этой плоскости (эту предельную плоскость называют соприкасающейся).
Далее условие (а) будем считать выполненным, если не оговорено противное. В случае, если условие (а) не выполнено, движение точки на прямолинейных участках естественно рассматривать отдельно.
Теперь введем в рассмотрение ортогональный базис тройку
~
(~τ, ~n, b) единичных взаимно-ортогональных векторов (ортов), исходящих из точки M1 , это ~τ = ~v/v орт касательной, ~n орт нормали, определяемый как единичный вектор, ортогональный вектору ~τ , лежащий в соприкасающейся плоскости и ориентированный
~ ×
в направлении вогнутости кривой в точке M1 , и, наконец, b = ~τ ~nорт бинормали.
Таким образом, с каждой парой (t, ~r(t)) мы связали базис его называют естественным базисом (а также естественной системой координат, натуральным базисом и т.п.).
Отметим, что одна и та же точка M траектории может соответствовать нескольким моментам времени в том смысле, что:
M = x(t1), y(t1), z(t1) = x(t2), y(t2), z(t2) = . . .
Натуральные системы, отвечающие парам (ti, ~r(ti)), i = 1, 2, . . ., могут быть различными. Тем самым может оказаться, что точке M пространства, через которую проходит траектория, будет сопоставлено несколько различных базисов. В этой связи напомним, что при введении криволинейных координат мы сопоставляли каждой точке ~r = (x, y, z) некоторой области D пространства Rn, n = 1, 2, 3 единственный базис.
Упражнение 3.2.
26
Перейти к оглавлению на странице: 256
1. Пусть пространственная кривая задана параметрически через движение ~r(t) = (x(t), y(t), z(t)). Получите фор-
~ |
|
мулы для ортов ~τ(t), ~n(t), b(t). |
|
2. Найти проекции векторов скорости и |
ускоре- |
~ |
~r(t) = |
ния на орты ~τ(t), ~n(t), b(t) для случая движения |
|
(sin t, cos t, t ln t). |
|
Разложение скорости по осям естественной системы координат очевидно: ~v = v~τ . В оставшейся части настоящего параграфа мы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˙ |
получим разложение по этим осям вектора ускорения w~ = ~v . |
|||||||||||||||
|
|
˙ |
t→0(Δ~v/ t), а вектор |
~v лежит в плос- |
|||||||||||
Так как w~ = ~v = lim |
|||||||||||||||
кости Π(M1,~v1, |
~v), то w~ |
лежит в соприкасающейся плоскости. |
|||||||||||||
Так как |
|
|
|
d |
|
|
|
dv |
|
|
d |
|
|
|
|
|
|
w~ = |
(v~τ) = |
~τ + v |
|
~τ, |
(3.2) |
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
dt |
|
|
dt |
dt |
|
||||||
а векторы w~ и ~τ |
лежат в соприкасающейся плоскости, то и вектор |
||||||||||||||
d~τ/dt = v−1(w~ |
− |
(dv/dt)~τ) |
лежит в соприкасающейся плоскости. |
||||||||||||
Так как |
|
|
|
||||||||||||
|
|
d |
|
|
d |
|
|
|
|
d |
|
|
|||
|
|
0 = |
1 = |
(τ~) = 2~τ |
|
~τ, |
(3.3) |
||||||||
|
|
|
|
|
|||||||||||
|
|
dt |
|
|
dt |
dt |
|
||||||||
то вектор d~τ/dt ортогонален вектору ~τ , а точнее направлен по вектору ~n.
Таким образом, из формулы (3.2) получаем: |
|
|||||||
|
|
|
|
|
|
|
~ |
(3.4) |
|
w~ = wτ ~τ + wn~n + wbb, |
|||||||
где |
= dt |
, wn = v dt |
, wb = 0. |
(3.5) |
||||
wτ |
||||||||
|
|
dv |
|
d~τ |
|
|
|
|
|
|
|
|
|
|
|
||
Величины wτ ~τ, |
wn~n |
|
|
|
|
~ |
и нормальным |
|
называют |
касательным |
|||||||
ускорениями (бинормальное ускорение wbb равно нулю). Величина wn может быть выражена через радиус кривизны траектории. Для того, чтобы получить это полезное в приложениях выражение, мы введем последовательно понятия естественной координаты, угла смежности, кривизны и радиуса кривизны.
Пусть t0 фиксированный момент времени, а t текущий момент, причем a < t0 < t < b. Одно из определений длины дуги
27
Перейти к оглавлению на странице: 256
s = s(t) траектории от точки ~r(t0) до точки ~r(t) следующее:
s(t) = Z t |
~r˙(t) dt = Z t v(t) dt = Z t |
(x˙ (t))2 + (y˙(t))2 + (z˙(t))2 dt. |
|||||
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
t0 |
t0 |
|
(3.6) |
|
|
|
|
|||||
|
|
s = s(t + t) − s(t), |
|
|
|||
Если |
|
~r = ~r(t + t) − ~r(t), то другое, |
|||||
эквивалентное, определение следующее: |
|
|
|||||
|
|
|
~r = (Δs)~τ + ~o(Δs), |
(Δt → 0). |
(3.7) |
||
Этими формулами мы будем пользоваться. Естественной координатой называют длину дуги s(t), отсчитываемую в сторону движения от некоторой точки (выше мы назвали эту точку символом ~r(t0)). Из равенств (3.7) и (3.6) соответственно получаем следующие формулы:
wτ = |
dv |
= s,¨ |
(3.8) |
||
|
|
||||
|
dt |
|
|||
~τ = |
d~r |
. |
(3.9) |
||
|
|||||
|
|
ds |
|
||
Углом смежности ϕ < π называют угол между ~τ(t) и ~τ(t+ |
t), |
||||
отсчитываемый от первого вектора ко второму.
Можно показать, что на регулярном участке траектории су-
ществует предел lim t→0(Δϕ/ |
t) = dϕ/dt, а тогда существует и |
||||||||||
величина |
|
|
|
|
|
|
|
|
|
||
K = |
dϕ |
= |
dϕ |
|
dt |
|
= v−1 |
dϕ |
, |
(3.10) |
|
ds |
dt ds |
dt |
|||||||||
|
|
|
|
|
|||||||
называемая кривизной траектории в точке ~r(t). Величину % = K−1 называют радиусом кривизны траектории в этой точке (для прямолинейных участков траектории радиус кривизны равен, по определению, +∞).
Лемма 3.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~τ |
= |
dϕ |
~n. |
|
|
|
(3.11) |
|||
|
|
|
|
|
|
dt |
|
|
|
|
|
||||
|
|
|
|
|
|
|
dt |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
обозначения |
~τ = ~τ(t + t) − ~τ(t), m~ = |
~τ/| ~τ|, |
|||||||||
|
Используя |
||||||||||||||
получаем |
|
|
|
sin |
|
m,~ |
|
||||||||
|
|
| ~τ| = 2 sin |
ϕ |
, |
~τ = 2 |
ϕ |
(3.12) |
||||||||
|
|
2 |
2 |
||||||||||||
28
