
- •ПРЕДИСЛОВИЕ
- •ЧАСТЬ I. ПРОСТРАНСТВА И КООРДИНАТЫ
- •Аффинные пространства
- •Аффинные евклидовы пространства
- •Аффинные координаты и преобразования
- •Криволинейные координаты
- •Криволинейные системы координат
- •Локальные базисы
- •ЧАСТЬ II. КИНЕМАТИКА
- •Кинематика точки
- •Коэффициенты Ламе. Проекции скорости точки на оси криволинейной системы координат
- •Проекции ускорения точки на оси ортогональной криволинейной системы координат
- •Описание движения точки в естественных координатах
- •Определение кривизны траектории точки по движению
- •Два примера движения точки
- •Кинематика твердого тела
- •Движение механической системы. Твердое тело. Число степеней свободы положения. Аффинное пространство и координаты, связанные с твердым телом
- •Группа движений аффинного евклидова пространства
- •Поступательное движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Плоское движение твердого тела
- •Движение твердого тела вокруг неподвижной точки
- •Угловая скорость, формула Эйлера и движение твердого тела в общем случае
- •Сложное движение
- •Сложное движение точки. Основные понятия
- •Относительная производная
- •Теорема сложения скоростей в сложном движении точки
- •Теорема сложения ускорений в сложном движении точки
- •Теорема о сложении угловых скоростей в сложном движении твердого тела
- •ЧАСТЬ III. ДИНАМИКА
- •Уравнения движения и основные законы динамики механической системы
- •Принцип детерминированности и уравнение Ньютона
- •Инерциальные системы координат
- •Сила и масса. Второй и третий законы Ньютона
- •Законы сил
- •Две задачи динамики
- •Уравнения движения механической системы
- •Теорема об изменении главного вектора количества движения
- •Уравнение движения центра инерции
- •Кинетический момент относительно неподвижной точки и теорема о его изменении
- •Движение точки в центральном поле сил
- •Изменение кинетического момента, вычисляемого относительно подвижного полюса
- •Работа силы и изменение кинетической энергии материальной точки
- •Условия потенциальности силового поля
- •Кинетическая энергия системы и теорема Кенига
- •Теорема об изменении кинетической энергии системы
- •Движение точки в центральном поле сил (продолжение)
- •Динамика твердого тела
- •Масса и плотность. Геометрия масс
- •Основные законы динамики твердого тела
- •Вращение твердого тела вокруг неподвижной точки
- •Уравнения движения свободного твердого тела
- •Динамика точки с переменной массой
- •Уравнение Мещерского
- •Две задачи Циолковского
- •ЧАСТЬ IV. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- •Общее уравнение механики
- •Cвязи, реакции. Обобщенные кооpдинаты
- •Изохронные ваpиации
- •Идеальные связи. Общее уравнение механики и принцип возможных перемещений
- •Общее уравнение механики в лагранжевых координатах
- •Уравнения Лагранжа
- •Уpавнения Лагpанжа II pода, их инваpиантность
- •Разрешимость уравнений Лагранжа II рода относительно старших производных
- •Обобщенный потенциал и уравнения Лагранжа II рода
- •Уравнения Лагранжа I рода и реакции идеальных связей
- •Канонические уравнения механики
- •Вывод канонических уравнений
- •Первые интегралы канонических уравнений
- •Метод Якоби решения канонических уравнений
- •Решение задачи о движении точки в центральном поле методом Якоби
- •Вариационные принципы механики
- •Дифференциальный принцип Даламбера-Лагранжа в декартовых переменных
- •Дифференциальный принцип Даламбера-Лагранжа в канонических переменных
- •Функционал и функция действия
- •Интегральный принцип наименьшего действия при изохронном варьировании (Принцип Гамильтона)
- •ЧАСТЬ V. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
- •Структуры и пространства
- •Группы, кольца, поля
- •Векторные пространства
- •Метрические пространства
- •Банаховы, гильбертовы и евклидовы пространства
- •Пространства Rn
- •Тензоры
- •Сопряженные пространства
- •Два определения тензора и их эквивалентность
- •Примеры тензоров
- •Алгебраические операции над тензорами
- •ЧАСТЬ VI. МАТЕРИАЛЫ ДЛЯ ЗАНЯТИЙ
- •Проверочные вопросы
- •Экзаменационные вопросы
- •Тесты
- •Упражнения
- •Литература
- •Предметный указатель
- •Оглавление

Перейти к оглавлению на странице: 256
ГЛАВА 2. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
В качестве пространства, в котором будут определены криволинейные координаты, мы рассматриваем здесь Rn . Мы будем рассматривать одновременно различные его экземпляры, поэтому будем использовать для них, наряду с Rn , также обозначения Rn(y),R1n(x) и т.п. (при x = (x1, . . . , xn), y = (y1, . . . , yn)). Частные случаи криволинейных координат в пространстве Rn хорошо известны. Это полярные, цилиндрические, сферические координаты и т.д. На этих примерах можно заметить, что задать какие-то криволинейные координаты в некоторой области D пространства Rn(y) означает поставить в соответствие каждой точке y = (y1, . . . , yn) этой области упорядоченный набор вещественных чисел x = (x1, . . . , xn) R1n , называемых координатами этой точки. Декартовы координаты, в этом смысле, ничем не отличаются от других координат. С другой стороны, ясно, что не всякое соответствие окажется полезным для введения криволинейных координат. Например, мало пользы в качестве системы координат могло бы принести соответствие, сопоставляющее каждой точке пространства Rn одну и ту же точку x R1n . Выделяя полезные свойства конкретных систем координат пришли к достаточно общему понятию криволинейной системы координат.
§1. Криволинейные системы координат
Криволинейной системой координат в области D Rn(y)
(область здесь, как обычно, – открытое связное множество) называют систему гладких функций (x1(y1, . . . , yn), . . . , xn(y1, . . . , yn)), задающих взаимно-однозначное отображение области D на некоторую область D1 R1n(x), причем эти функции таковы, что отличен от нуля во всех точках области D якобиан
J(y) = det |
∂x1/∂y. |
1 |
. .. . |
∂xn/∂y. |
1 |
. |
|
(1.1) |
||
|
∂x1/∂yn |
. . . |
∂xn/∂yn |
|
|
|
|
|||
Отличие от нуля якобиана J(y) |
при |
|
всех |
y |
|
D |
||||
гарантирует, что отображение |
|
f−1(x), |
обратное |
к |
f(y) |
= |
||||
12
Перейти к оглавлению на странице: 256
(x1(y1, . . . , yn), . . . , xn(y1, . . . , yn)), также является гладким (это следствие теоремы о неявных функциях).
Таким образом, криволинейная система координат задается двумя гладкими, взаимно-обратными отображениями f(y) и
f−1(x), устанавливающими гомеоморфизм между множествами
D = f−1(D1) и D1 = f(D).
Гладкость – понятие гибкое, нам следует уточнить его. Отображение f : D → R1n называют гладким отображением класса
Cr(D) при 1 6 r < ∞, или r = ∞, или r = ω , если оно дифференцируемо до порядка r включительно, или бесконечно дифференцируемо, или аналитично соответственно. Часто гладкое отображение какого-то класса называют просто гладким отображением, а класс гладкости уточняют при необходимости. Гладкий гомеоморфизм класса Cr(D) между D и D1 называют диффеоморфизмом класса Cr(D), а множества D и D1 , при существовании такого диффеоморфизма, называют диффеоморфными.
Итак, криволинейная система координат в области D Rn это некоторый диффеоморфизм f : D → R1n с ненулевым якобианом.
Так как мы собираемся пользоваться различными системами координат и, в частности, переходить от одной системы координат к другой, то должны рассмотреть общее понятие замены координат.
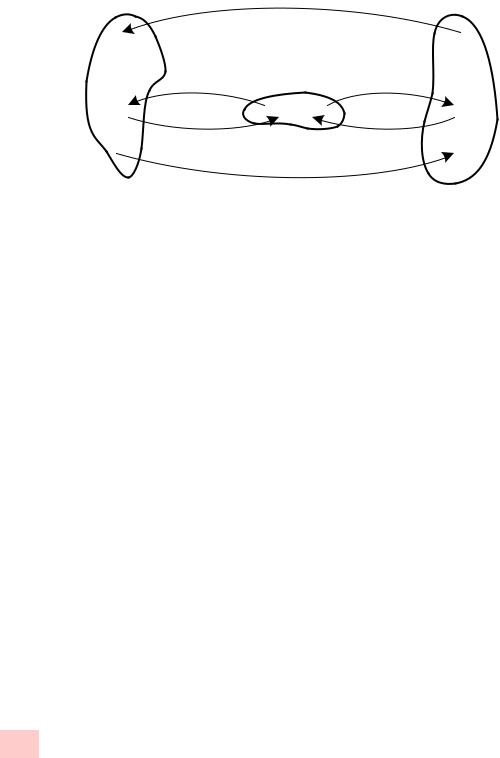
Пусть y = (y1, . . . , yn) Rn(y), |
и в области D Rn(y) |
|||||||||||
две системы координат x(y) = |
(x1(y), . . . , xn(y)) |
и z(y) = |
||||||||||
(z1(y), . . . , zn(y)) (Рис. 1.1) заданы отображениями f |
: D |
→ |
D1 |
|
||||||||
R1n(x) и g : D → D2 R2n(z). |
|
|
|
|
|
|
|
|||||
Заменой координат x на z (или z на x) называется отоб- |
||||||||||||
ражение ψxz : D1 → D2(ψzx : D2 |
→ D1), задаваемое фор- |
|||||||||||
мулой ψxz |
= g ◦ f−1 |
(соответственно, |
ψzx |
= f ◦ g−1 ), то есть |
||||||||
ψxz(x) = g |
f−1 (x) ψzx(z) = f(g−1(z) |
) (Рис. 1.1). |
|
|
|
|
||||||
|
|
= g |
◦ |
f−1 |
|
|
|
D получает |
вме- |
|||
При замене ψxz |
|
точка y |
|
|||||||||
сто криволинейных координат (x1(y), . . . , xn(y)) новые координаты
(z1(y), . . . , zn(y)).
Можно показать, что замена ψxz : D1 → D2 диффеоморфизм с ненулевым якобианом, то есть это криволинейная система координат в D1 R1n(x).
Если задана декартова система координат, то задание новой криволинейной системы координат удобно трактовать как замену
13
Перейти к оглавлению на странице: 256
R1n (x1 ,…, xn ) |
ψz x = f g−1 |
|
R2n (z1 ,…, zn ) |
||
|
|
|
|
||
|
f |
Rn (y1 ,…, yn ) |
g |
|
|
D1 |
D |
D2 |
|||
|
|
||||
|
|
|
|
||
|
f −1 |
|
g−1 |
|
|
|
ψx z = g f −1 |
|
|||
|
|
|
|
||
Рисунок 1.1
и задавать формулами замены координат. В качестве примера рассмотрим цилиндрическую систему координат в R3 (Рис. 2.2). Рассмотрим R3(y), R13(x) при y = (y1, y2, y3), x = (x1, x2, x3) и используем обозначения:
% = y1, ϕ = y2, z = y3, |
|
D = (%, ϕ, z) R3 | % > 0, ϕ [0, 2π), z R . |
(1.2) |
Формулы |
|
x1 = % cos ϕ, x2 = % sin ϕ, x3 = z |
(1.3) |
определяют гладкое отображение f : D → D1 R13(x) с якобианом:
|
cos ϕ |
sin ϕ |
0 |
|
|
|
− |
% sin ϕ |
% cos ϕ |
0 |
(1.4) |
||
J(%, ϕ, z) = det |
|
= %. |
||||
|
|
0 |
0 |
1 |
|
|
Как видим, формулы (1.3) задают криволинейную систему координат в области D R3(%, ϕ, z), а значит и в области D1
R13(x).
§2. Локальные базисы
В механике фиксированную декартову систему координат в R3 часто обозначают Oxyz , а упорядоченный набор координат точ-
~ |
~ |
~ |
ки рассматривают как радиус-вектор ~r = (x, y, z) = xi |
+ yj |
+ zk , |
14

Перейти к оглавлению на странице: 256
~ ~ ~
где i, j, k орты системы Oxyz . Криволинейные координаты обозначим ~q = (q1, q2, q3) и будем задавать их формулами qi = qi(~r),
~r = (x, y, z) D, i = 1, 2, 3, то есть ~q = ~q(~r), или x = x(~q), y = y(~q), z = z(~q), ~r = ~r(~q) при ~q = (q1, q2, q3) Q = { ~q | ~q = ~q(~r), ~r D }, причем предполагается, что ~q(~r(~q)) = ~q, ~r(~q(~r)) = ~r в областях Q и D соответственно.
z 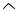
~
q3
x
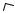 τr3 (q10 )
τr3 (q10 )
|
|
|
) |
|
|
|
z |
|
y |
, 0 |
|
( 0 |
0 |
||
x |
, |
||
|
|
|
|
(q20 ) |
|
|
|
r |
|
(q30 ) |
|
τ1 |
|
||
|
|
||
~
q1
Рисунок 2.1
1
τr2
~
q2
y
Теперь мы введем в рассмотрение понятия координатной поверхности, координатной линии, локального базиса и ортогональности криволинейной системы координат. Это позволит нам в дальнейшем проектировать различные векторы (скорость, ускорение и т.п.) на оси криволинейной системы координат, то есть на оси упомянутого локального базиса. Наиболее простыми оказываются формулы проекций векторов на оси ортогональных криволинейных систем координат.
Пусть ~q0 = (q1,0, q2,0, q3,0) Q, ~r0 = ~r(~q0) = (x0, y0, z0), тогда три множества
(qi,0) = { (x, y, z) D | qi(x, y, z) = qi,0 } , i = 1, 2, 3 |
(2.1) |
называют координатными поверхностями криволинейной системы координат ~q = (q1, q2, q3) в точке (q1,0, q2,0, q3,0), а множества
q˜3 = (q1,0) ∩ (q2,0), q˜2 = (q1,0) ∩ (q3,0), q˜1 = (q2,0) ∩ (q3,0) (2.2)
15
Перейти к оглавлению на странице: 256
ее координатными линиями в этой точке. Ясно, что
(q1,0) ∩ (q2,0) ∩ (q3,0) = { (x0, y0, z0) } . |
(2.3) |
В соответствии с определением криволинейной системы координат, ее якобиан отличен от нуля в каждой точке области опреде-
ления Q. Три вектора |
∂ ~r |
, |
|
∂ ~r |
, |
∂ ~r |
составляют строки матрицы |
∂ q1 |
∂ q2 |
∂ q3 |
|||||
этого якобиана и поэтому не могут быть нулевыми. Эти векторы являются касательными в точке ~q0 = (q1,0, q2,0, q3,0) Q к линиям q˜1 , q˜2 , q˜3 соответственно.
z  [z]
[z]
ϕ~ |
[ϕ] |
r |
er2 |
e3 |
(x0 , y0 , z0 ) |
|
er |
ρ~ |
1 |
|
|
|
|
~ |
[ρ] |
|
|
|
|
|
|
|
|
z |
|
x |
ϕ |
ρ |
|
y |
|
|
|
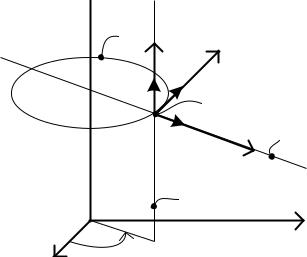
Рисунок 2.2
Действительно, координатная кривая q˜i в точке (q1,0, q2,0, q3,0) параметризуется переменной qi , то есть, например, для линии q˜1
можно положить ~r = ~r(q1, q2,0, q3,0), и тогда производная |
∂ ~r |
дает |
|
||
направление касательной к этой кривой. |
∂ q1 |
|
|
|
|
Совокупность трех векторов (~τ1, ~τ2, ~τ3) единичной |
длины, |
|
−1
определяемых формулой ~τi |
= |
|
∂ ~r |
|
∂ ~r |
, i = 1, 2, 3 называют |
∂ qi |
∂ qi |
|||||
|
|
|
|
|
|
|
локальным базисом в точке ~q0 = (q1,0, q2,0, q3,0) рассматриваемой криволинейной системы координат. Если векторы ~τ1, ~τ2, ~τ3 взаимно ортогональны в точке ~q0 = (q1,0, q2,0, q3,0) (в каждой точке области Q), то базис и сама криволинейная система называются ортогональными в этой точке (в области Q).
16

Перейти к оглавлению на странице: 256
Получим условия ортогональности криволинейной системы
координат. Так как ни один из векторов |
∂ ~r |
, |
∂ ~r |
, |
|
∂ ~r |
не мо- |
∂ q1 |
∂ q2 |
∂ q3 |
|||||
жет быть нулевым, то условия ортогональности локального базиса
~τ1 ~τ2 = 0, ~τ1 ~τ3 = 0, ~τ2 ~τ3 |
= 0 эквивалентны равенствам |
∂ ~r |
|
∂ ~r |
= 0, |
|||||||||||||||||||
∂ q1 |
|
|||||||||||||||||||||||
|
∂ ~r |
|
∂ ~r |
= 0, |
|
∂ ~r |
|
|
∂ ~r |
= 0, а значит и равенствам: |
∂ q2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂ q1 ∂ q3 |
∂ q2 ∂ q3 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
∂ x ∂ x |
|
|
∂ y ∂ y |
|
∂ z ∂ z |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
= 0, i, j = 1, 2, 3, i 6= j. |
(2.4) |
|||||||
|
|
|
∂ qi ∂ qj |
∂ qi ∂ qj |
∂ qi |
∂ qj |
||||||||||||||||||
Упражнение 2.1. Показать, что цилиндрическая система
координат ортогональна во всей своей области определения (Рис. 2.2).
17
