Перейти к оглавлению на странице: 256

тела в момент t при его вращении вокруг неподвижной оси.

§5. Плоское движение твердого тела

Преобразование координат в плоском движении

Изменим некоторые обозначения по сравнению с §1. Точку Mτ твердого тела будем обозначать просто M , имея в виду, что это его произвольная точка. Координаты (xτ1 , xτ2 , xτ3 ), (y1τ , y2τ , y3τ ) в непо-

~ ~ ~

движном репере (O,~e1,~e2,~e3) и подвижном репере (M0, i1, i2, i3) будем обозначать теперь (ξ, η, ζ) и (x, y, z) соответственно. Сами

~ ~ ~

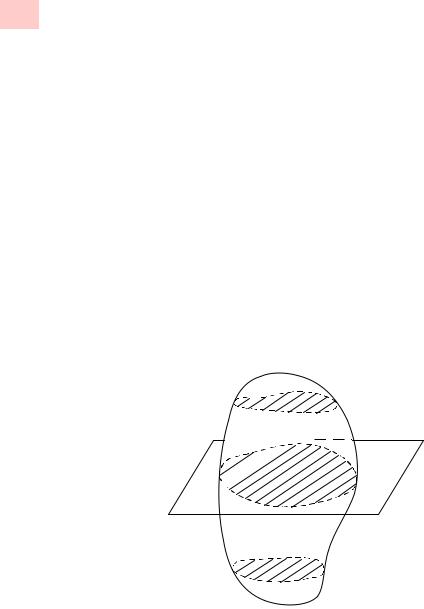
реперы также будем обозначать иначе: (O,~eξ,~eη,~eζ) и (M0, i, j, k). Как мы уже говорили в §2, плоским или плоско-параллельным называют такое движение твердого тела, при котором в неподвижном пространстве существует плоскость α (плоскость параллелизма) такая, что сечение Q(α, t0) (состоящее из точек твердого тела, лежащих в α в момент t0 J ) принадлежит α при всех t J (см. рис. 5.1)

1

Q

α

Рисунок 5.1

Начало O неподвижного репера вместе с исходящими из него ортами ~eξ,~eη поместим в эту плоскость. Если, как и в §2, предположить, что

~ ~

i(t), j(t) также лежат в плоскости α. Здесь мы не будем предпола-

53

Перейти к оглавлению на странице: 256

гать, что выполнено условие (5.1), а просто поместим начало M0(t0)

~~

иорты i(t0), j(t0) в плоскость α, тогда они будут оставаться там при всех t J .

Как следует из формулы (2.10), связь между координатами точки M в подвижном и неподвижном репере следующая:

Мы видим, что координата ζ остается постоянной во времени, а преобразование координат ξ, η происходит по формулам:

Формулы (5.3) дают связь между координатами ξ, η и x, y точки M тела, лежащей в плоскости α.

Таким образом, при изучении плоского движения твердого тела можно ограничиться рассмотрением движения плоской фигуры Q на плоскости α, то есть твердого тела в E2 . Для того, чтобы

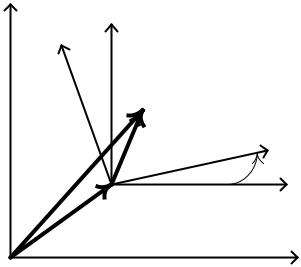
(рис. 5.2). Проектируя это равенство на неподвижные оси приходим к искомым соотношениям:

~

где (ξ0, η0) M0 , а ϕ угол между ~eξ и i (отсчитываемый от ~eξ ). Из формул (5.4) следует, что координаты ξ, η любой точки M твердого тела вполне определяются положением направленного от-

~

резка (M0, M0 + i). Действительно, если, например, это положение задано координатами концов отрезка, то тем самым заданы и величины ξ0, η0, ϕ. С большей общностью можно сказать, что координаты ξ, η любой точки M твердого тела вполне определяются положением любого направленного отрезка (A, B), принадлежащему этому телу (сечению Q тела плоскостью α), то есть при изучении плоского движения твердого тела можно ограничиться рассмотрением движения любого отрезка (A, B) при A 6= B в пространстве

E2 .

54

Перейти к оглавлению на странице: 256

Две геометрические теоремы о плоском движении

В теоремах настоящего параграфа речь пойдет о перемещениях твердого тела, поэтому вспомним вначале это понятие. В §1 мы сказали, что перемещением механической системы за время от t1 до

t2 (из положения {aτ }τ T в положение {bτ }τ T ) называют семей-

−−−−−−−−−−→

ство векторов {Dτ (t1), Dτ (t2)}τ T (соответственно, семейство век-

−−−→

торов {aτ , bτ }τ T ). Если воспользоваться понятием закрепленного вектора, то в приведенном определении вместо семейства векторов можно говорить о семействе закрепленных векторов. Кроме того, в §2 мы выяснили, что всякому перемещению механической системы твердого тела соответствует преобразование D : E3 → E3 по формуле (2.6).

Определим композицию перемещений механической системы. Если перемещения преобразования D1, D2 , то их композици-

Нам потребуется два специальных вида плоских перемещений твердого тела, то есть его перемещений в E2 : поступательное перемещение и поворот вокруг точки (полюса). Говорят, что переме-

55

Перейти к оглавлению на странице: 256

щение твердого тела является поступательным (поворотом вокруг полюса точки C ), если из положения {aτ }τ T в положение {bτ }τ T оно может перейти, двигаясь поступательно (соответствен-

но, вращаясь вокруг C ).

−−−−→

Пусть C1, C2 перемещение точки C твердого тела при его

движении из положения {aτ }τ T в положение {bτ }τ T . Тогда по-

−−−−−−−−−−→

−−−−→

ступательное перемещение {aτ , aτ + C1, C2}τ T будем называть поступательным перемещением твердого тела вместе с точкой C .

Теорема 5.1. (Шаль) Пусть Π некоторое перемещение

твердого тела в E2 (то есть плоское перемещение). Пусть C произвольная точка этого тела в E2 (под телом здесь понимается экземпляр E2 , жестко связанный с телом), а C1, C2 ее начальное и конечное положения в перемещении Π. Тогда:

1. Перемещение Π можно представить в виде композиции

где Πпост(C) поступательное перемещение тела вместе с точкой C , а Πвращ(Ci) вращательное перемещение тела вокруг точки Ci ;

2. Углы поворота перемещений Πвращ(C1), Πвращ(C2) равны и их общее значение не зависит от выбора полюса C .

Теорема 5.2. (Эйлер) Любое непоступательное перемеще-

ние твердого тела в E2 есть вращательное перемещение вокруг некоторого полюса C , называемого центром вращения.

Упражнение 5.1. Докажите теоремы 5.1, 5.2.

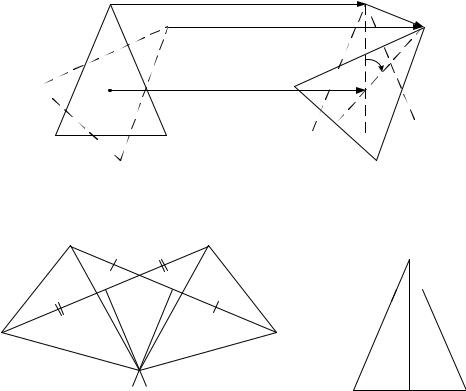
Обе теоремы геометрически очевидны (рис. 5.3).

Фоpмула Эйлеpа и ее следствие

Пусть ~r = ~r(t) радиус-вектор произвольной точки плоского сечения твердого тела в неподвижной системе координат. Рас-

56

Перейти к оглавлению на странице: 256

M2

C1

C2

C

B B′

C

Рисунок 5.3

поступательного перемещения вместе с полюсом A, и ~rвращ величины перемещения вращения вокруг оси, проходящей через полюс A (в его начальном или конечном положении) и перпендикулярной плоскости параллелизма. По формуле (4.1), получаем

от выбора полюса A и точки M . Здесь ϕ~(t) означает полярный

−→

угол, сонаправленный с ϕ. Вектор ω~ называют угловой скоро-

стью твердого тела при его плоском движении. Его величина равна

−→

ω(t) = dϕ(t)/dt, а направлен он как и ϕ. Разделив равенство (5.6)

на t и перейдя к пределу при t → 0, получим формулу Эйлера:

57

Перейти к оглавлению на странице: 256

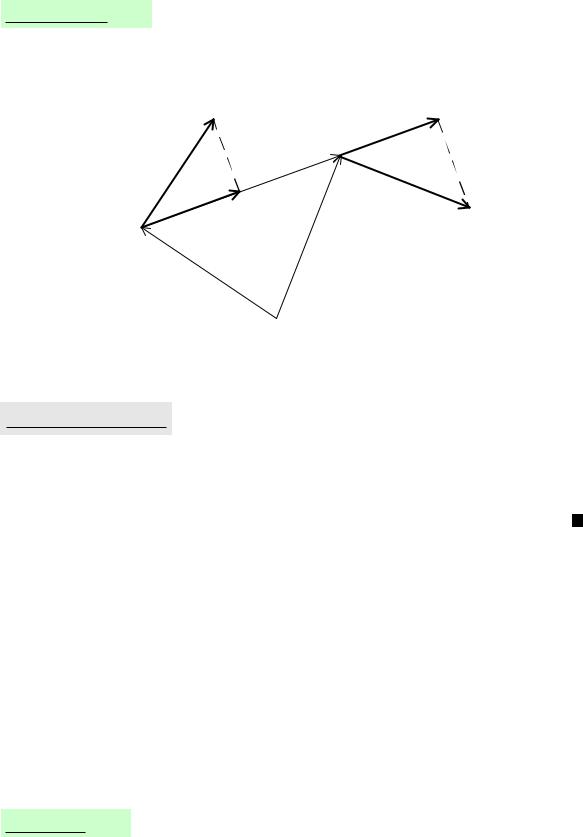
Следствие 5.1. При плоском движении твердого тела, проекции скоростей концов отрезка, расположенного в плоскости параллелизма, на направление этого отрезка равны между собой.

Доказательство. По формуле Эйлера получаем, что ~vB = ~vA +

−−→

ω~ × (~rB − ~rA). Так как ~rB − ~rA = AB , и ω~ × (~rB − ~rA) (~rB − ~rA),

то равна нулю проекция второго слагаемого справа на направление

−−→

AB . Что и требовалось.

Центр скоростей. Центроиды. Теоpема Пуансо

Если плоское движение твердого тела является поступательным, то скорости всех его точек равны между собой, и общее значение этих скоростей можно назвать скоростью поступательного движения твердого тела. Если эта скорость равна нулю, то движение называют состоянием покоя.

Распределение скоростей точек твердого тела дается формулой Эйлера (5.7). Из нее, в частности, следует, что при поступательном движении твердого тела его угловая скорость равна нулю. Как мы сейчас покажем, при непоступательном движении твердого тела одна и только одна точка твердого тела имеет нулевую скорость.

Теорема 5.3. Пусть движение твердого тела является плоскопараллельным, а плоскость Q (подвижное простран-

58

Перейти к оглавлению на странице: 256

ство) жестко связана с этим телом и движется в плоскости параллелизма α. Тогда, если в данный момент времени угловая скорость тела не равна нулю (то есть его движение не является поступательным в этот момент), то существует единственная точка C плоскости Q, скорость которой равна нулю в этот момент.

Доказательство. Мы должны показать, что существует единственная точка M плоскости Q такая, что ~vM = ~vA + ω~ × (~rM −

~

~rA) = 0. Если последнее равенство рассмотреть как уравнение от-

~ − −2 ×~ b следует, что ~x = a ~a b.

Точку C Q из теоремы 5.3 называют мгновенным центром скоростей (или просто центром скоростей) в плоском движении твердого тела (в этот момент). Если в формуле Эйлера за полюс взять C , то получим:

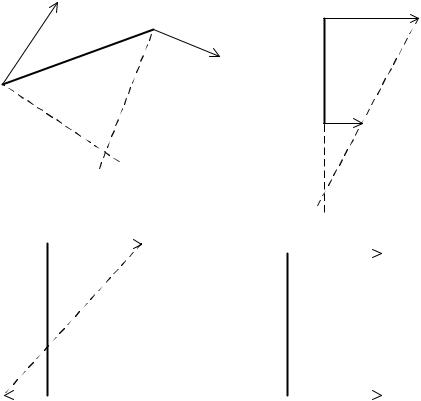
Формула (5.8) идентична формуле Эйлера для скоростей точек твердого тела при его вращении вокруг неподвижной оси, проходящей через точку C Q и перпендикулярной плоскости Q, поэтому центр скоростей C называют также центром вращения. Если заданы скорости двух различных точек твердого тела A, B Q в его плоскопараллельном непоступательном движении, то мгновенный центр скоростей легко находится геометрически (рис. 5.5).

Из формулы (5.8) следует, что ~v (~r −~rC), то есть скорости точек тела (кроме центра скоростей) перпендикулярны их радиусвекторам, исходящим из мгновенного центра C . Имея это в виду, при известных направлениях скоростей точек A, B , проведем через них прямые lA, lB , ортогональные векторам скоростей в этих точках. Эти прямые либо пересекаются, либо нет возможные варианты разобьем на четыре случая:

(а) прямые lA, lB пересекаются в единственной точке это и будет центр скоростей C ;

59

Перейти к оглавлению на странице: 256

C

C

Рисунок 5.5

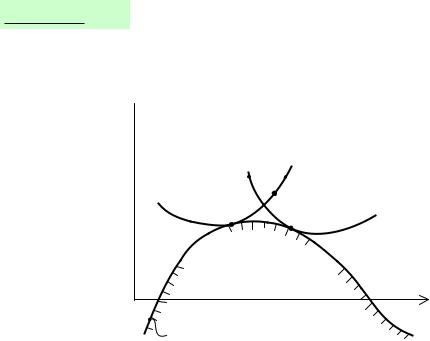
(б) закрепленные векторы (A,~vA), (B,~vB) параллельны, направлены в одну сторону и не равны по величине в этом случае прямые lA, lB совпадают; через концы рассматриваемых закрепленных векторов (то есть через точки A + ~vA, B + ~vB ) проведем прямую l, точка пересечения этой прямой с прямой lA и будет центром скоростей C ;

(в) закрепленные векторы (A,~vA), (B,~vB) параллельны и направлены в разные стороны в этом случае прямые lA, lB совпадают; через концы рассматриваемых закрепленных векторов (то есть через точки A+~vA, B +~vB ) проведем прямую l, точка пересечения этой прямой с прямой lA (она лежит на отрезке, соединяющем точки A, B ) и будет центром скоростей C ;

(г) закрепленные векторы параллельны, направлены в одну сторону и равны по величине в этом случае движение твердого тела поступательное и для него понятие центра скоростей не определено.

60

Перейти к оглавлению на странице: 256

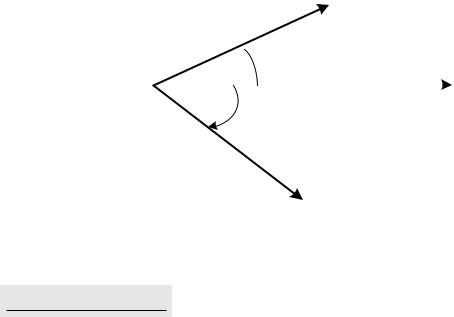
Геометрическое место мгновенных центров скоростей в неподвижной плоскости α (в подвижной плоскости Q) называют

неподвижной центроидой (соответственно подвижной центроидой). Обе центроиды некоторые кривые. Если рассмотреть их в неподвижном пространстве (то есть в плоскости α с репером (O,~eξ,~eη)), то положение подвижной центроиды будет изменяться с течением времени t, а положение неподвижной центроиды не зависит от t. В каждый момент t эти кривые имеют одну общую точку C(t) мгновенный центр скоростей.

Теорема 5.4. (Пуансо) При плоском непоступательном движении твердого тела подвижная центроида катится без скольжения по неподвижной.

η

подвижная центроида в моменты t1 и t2

C(t1 ) C(t2 )

ξ

неподвижная центроида

Рисунок 5.6

Пояснение. Мгновенный центр C(t) (в момент t и в достаточно малой своей окрестности это единственная общая точка центроид) с изменением t перемещается по обеим центроидам со

ˆ

скоростями ~v(t),~v(t). Содержание теоремы Пуансо состоит в том,

ˆ

что ( t J) (~v(t) = ~v(t)), где J промежуток, на котором рассматривается движение твердого тела.

Геометрическая интерпретация плоского движения твердого тела качением подвижной центроиды по неподвижной имеет техническое применение: если необходимо осуществить какое-то плоское движение твердого тела, то можно изготовить соответствующие

61

Перейти к оглавлению на странице: 256

этому движению подвижную и неподвижную центроиды (жестко связанные с твердом телом и неподвижным основанием соответственно), и тогда качение без проскальзывания подвижной центроиды по неподвижной придаст твердому телу искомое движение.

Для того, чтобы вывести уравнения центроид, обратимся к формулам (5.4). Дифференцируя их по t, получаем:

то есть формуле Эйлера для скорости точки M , когда за полюс принята точка M0 . Уравнение неподвижной центроиды получим из формул (5.10), если положим в них ξ˙ = 0, η˙ = 0, ξ = ξC, η = ηC :

Это уравнения в параметрическом задании, от параметра t зависят величины ξ0, η0, ϕ.

Уравнение подвижной центроиды получим из формул (5.9), если положим в них ξ˙ = 0, η˙ = 0, x = xC, y = yC :

xC = (ξ˙0 sin ϕ − η˙0 cos ϕ)ϕ˙−1, yC = (ξ˙0 cos ϕ + η˙0 sin ϕ)ϕ˙−1. (5.13)

Упражнение 5.3. Докажите теорему Пуансо.

Ускорение точек твердого тела в плоском движении

Дифференцируя формулу Эйлера (5.7) по t, получаем:

62

Перейти к оглавлению на странице: 256

Так как ω~ (~r − ~rA) согласно определению ω~ , то получаем:

Векторы ~ε, w~1, w~2 называют соответственно угловым ускорением, вращательным ускорением и осестремительным ускорением твердого тела в плоском движении.

Спроектируем равенство (5.14) на неподвижные орты ~eξ,~eη и

~ ~

на подвижные орты i, j :

Так как проекции wA,ξ, wA,η вектора w~A на неподвижные ор-

¨

ты равны ξA, η¨A , то его проекции wA,x, wA,y на подвижные орты, повернутые относительно неподвижных ортов на угол ϕ, равны:

¨ −¨

wA,x = ξA cos ϕ + η¨A sin ϕ, wA,y = ξA sin ϕ + η¨A cos ϕ. (5.20)

Формулы (5.19) запишем также в следующей, комплексной форме:

Мгновенным центром ускорений в плоском движении твердого тела называют точку D(t) плоскости Q (подвижного пространства, см. теорему 5.3), ускорение которой в данный момент t равно нулю.

Отметим, что если в качестве полюса A выбрать центр ускорений D(t), то формула (5.14) для данного момента t совпадет с аналогичной формулой для случая вращения твердого тела вокруг неподвижной оси, проходящей через D(t) и перпендикулярной плоскости Q. Отметим также, что центр ускорений понятие менее употребительное, чем центр скоростей.

Теорема 5.5. Пусть движение твердого тела является плоскопараллельным, а плоскость Q (подвижное пространство см. теорему 5.3), жестко связана с этим телом и

63

Перейти к оглавлению на странице: 256

движется в плоскости параллелизма α. Пусть используются обозначения (5.21), а ϕ угол между подвижными и неподвижными ортами.

Тогда, при ϕ¨2 + ϕ˙4 6= 0, существует единственный мгновенный центр ускорений с координатами z = zD , и имеют место формулы:

считываемый от последнего (см. рис. 5.7).

D

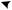ψ >0

D

Рисунок 5.7

Доказательство. Полагая z = zD, W = WD = 0 в формуле

то есть первая из формул (5.22) доказана.

~

Начало подвижного репера поместим в полюс A, а орт i сонаправим с w~A (рис. 5.8). Тогда WA = wA и первая из формул (5.22) примет следующий вид:

64