Перейти к оглавлению на странице: 256

ГЛАВА 3. КИНЕМАТИКА ТОЧКИ

Движение, скорость и ускорение точки находятся в ряду основных понятий механики. Их вычисление или исследование не всегда целесообразно в декартовых координатах. В настоящей главе мы получим формулы для проекций скорости и ускорения точки на оси криволинейной (§1, §2) и естественной (§3, §4) систем координат и рассмотрим два простых, но важных примера – движение точки по прямой и по окружности (§5). Но до этого необходимо ввести в рассмотрение для модели кинематики точки понятия пространства, механической системы, движения, перемещения, скорости и ускорения.

В качестве пространства будем использовать аффинное евклидово пространство En, n = 1, 2, 3; точку этого пространства будем представлять радиус–вектором ~r в какой-либо декартовой системе

Механической системой в момент t0 или положением системы в момент t0 будем называть точку M0 в En, n = 1, 2, 3. Пусть J – промежуток на R. Движением этой системы (точки)

будем называть дважды непрерывно дифференцируемую функцию D : J −→ En времени t такую, что D(t0) = M0 . В частности, если точка этого пространства представлена радиус–вектором ~r в какойлибо декартовой системе координат, то ее движение представляется вектор–функцией ~r : J −→ Rn . В этом случае скоростью и ускорением точки в этом движении называют соответственно

˙ ¨

вектор–функции ~v = ~r, w~ = ~r, а траекторией точки называют кривую {~r(t) Rn |t J}.

Замечание 1. Наряду с df/dt, d2f/dt2, . . . для производных f по аргументу t, мы используем, как это принято в механике, и обозначения f˙, f¨, . . ..

§1. Коэффициенты Ламе. Проекции скорости точки на оси криволинейной системы координат

Так как

19

Перейти к оглавлению на странице: 256

где

Величины Hm (иногда удобнее обозначение Hqm ) называют коэффициентами Ламе. При помощи формул (1.1), (1.3) мы найдем направляющие косинусы осей локального базиса криволинейной системы координат ~q = (q1, q2, q3) относительно осей декартовой системы Oxyz и разложение вектора скорости точки в этом базисе. Из формулы (1.3) получаем:

(q1, q2, q3) называют ~q = (q1(t), q2(t), q3(t)) – дважды непрерывно дифференцируемую вектор–функцию аргумента t (времени) на промежутке J R.

Функции q˙1, q˙2, q˙3 и q¨1, q¨2, q¨3 называют соответственно обобщенными скоростями и ускорениями точки в этом движении, а кривую (множество точек) {(q1, q2, q3) R3 | q1 = q1(t), q2 = q2(t), q3 = q3(t), t J} – траекторией точки в криволинейных координатах.

Теорема 1.1. Пусть ~q = (q1(t), q2(t), q3(t)) – движение точки,

20

Перейти к оглавлению на странице: 256

то из формулы (1.1) получаем:

откуда и следует (1.5).

Следствие 1.1. Если криволинейная система ортогональна, то

q

v = (H1q˙1)2 + (H2q˙2)2 + (H3q˙3)2,

(1.8)

cos (~v, ~τm) = Hmq˙mv−1, m = 1, 2, 3.

Пример 1.1. Рассмотрим цилиндрическую систему координат. Так как

∂x∂% = cos ϕ, ∂y∂% = sin ϕ, ∂%∂z = 0,

то легко проверить, что условия ортогональности (2.4) главы 2 выполнены.

21

x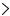

Рисунок 1.1

§2. Проекции ускорения точки на оси ортогональной криволинейной системы координат

qm , то есть на вектор ~τm , и используются обозначения (2.1) и T = 12v~ = 12 v2 . Тогда, если криволинейная система коор-

22

Перейти к оглавлению на странице: 256

где Eqm (T ) – линейный дифференциальный оператор (оператор Эйлера–Лагранжа), определяемый равенством

поэтому для доказательства теоремы мы должны показать, что

Так как

то равенство (2.5) будет доказано если в (2.6) использовать формулы:

Остается доказать эти равенства. Второе из них следует непосредственно из формулы (2.1), а первое – из очевидных равенств:

(получено по формуле дифференцирования сложной функции). Что и требовалось.

23