§3. Элементарные преобразования системы линейных алгебраических уравнений.

Понятие эквивалентной системы. Рассмотрим две системы линейных алгебраических уравнений с одинаковым количеством неизвестных .

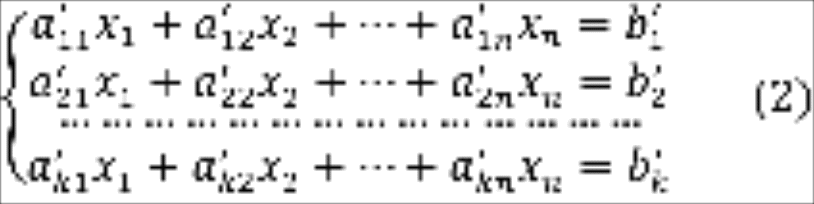
Заметим, что числа могут не совпадать. Т.е. количество уравнений системы (1) может не совпадать с количеством уравнений системы (2).

Системы (1) и (2) с одинаковым количеством неизвестных называются эквивалентными, если каждое решение системы (1) является решением системы (2) и наоборот – каждое решение системы (2) является решением системы (1).

Элементарные преобразования системы. Элементарными преобразованиями системы называются преобразования следующих трёх типов.

1. Перестановка местами любых двух уравнений системы;

2. Умножение любого уравнения системы на любое отличное от нуля число;

3. Прибавление к одному уравнению системы другого её уравнения, умноженного на любое число.

Заметим, что элементарные преобразования системы означают элементарные преобразования сток её расширенной матрицы.

Теорема 3.1. Элементарные преобразования системы линейных алгебраических уравнений приводят её к эквивалентной системе.

Справедливость теоремы 3.1 непосредственно вытекает из определения эквивалентных систем.

§4. Системы с верхней трапециевидной матрицей.

Рассмотрим систему линейных алгебраических уравнений с верхней трапециевидной матрицей

Возможны следующие четыре случая.

Случай 1. Пусть матрица имеет вид

В случае 1 система (1) имеет вид

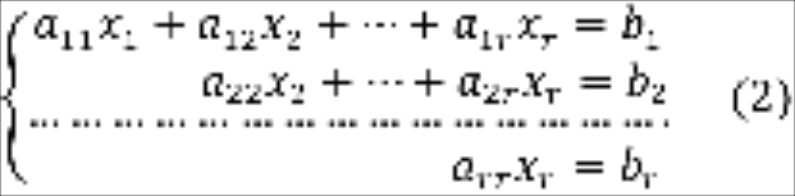
При этом расширенная матрица системы (2) имеет вид

.

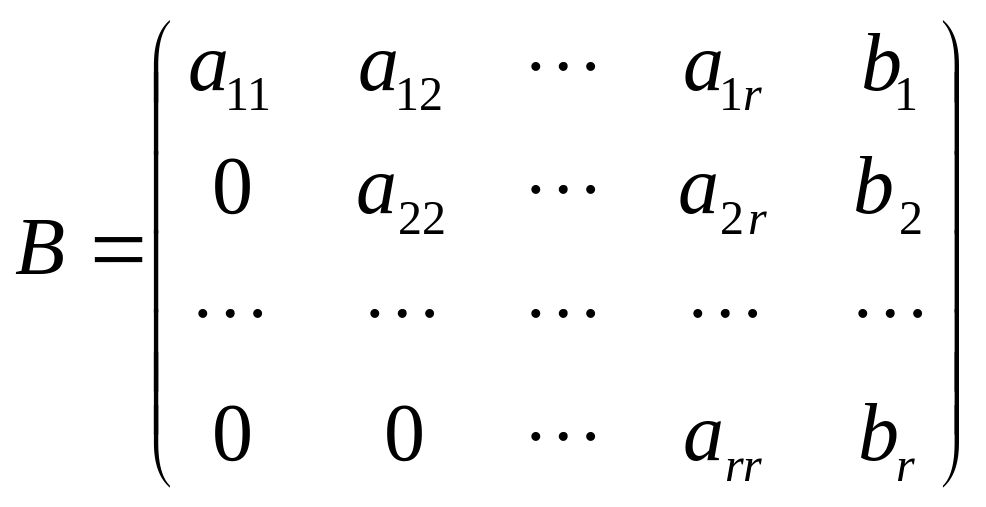Легко заметить, что .

Найти решение системы (2) не представляет труда: решая последовательно уравнения системы снизу вверх, мы каждый раз будем иметь дело с уравнением, содержащим только одно неизвестное.

Заметим, что в случае 1 система (2), а стало быть и система (1) имеет единственное решение.

Случай 2. Пусть матрица имеет вид

В случае 2 система (1) имеет вид

А расширенная матрица - вид

.

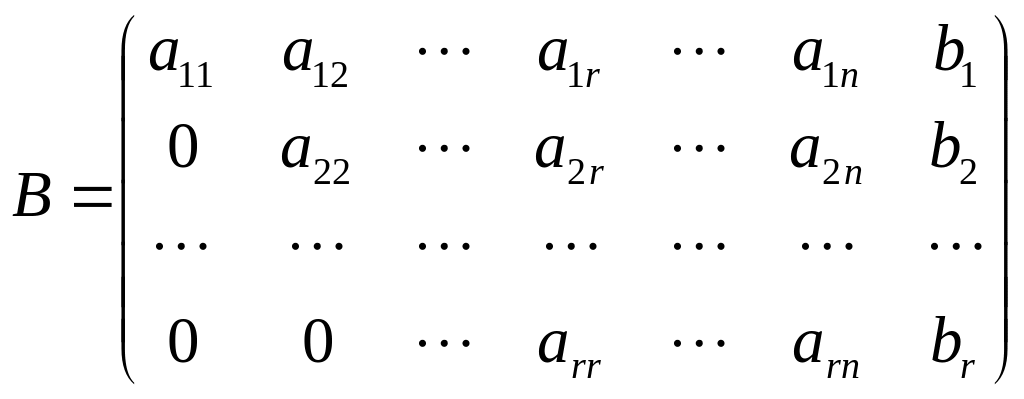Как и в случае (1), .

Назовём неизвестные – главными неизвестными, а – свободными.

Перенося в уравнениях системы (3) все слагаемые, содержащие свободные неизвестные в правую часть, получим

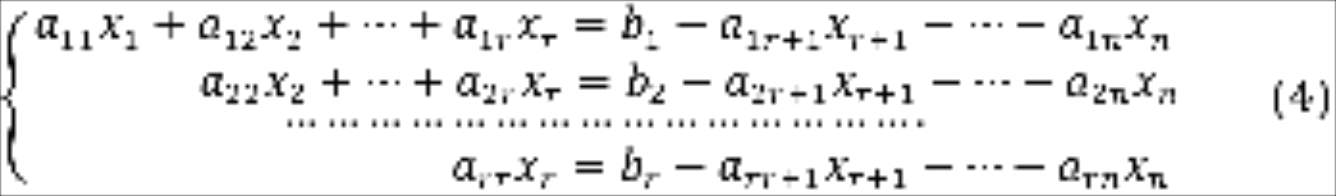
Решая последовательно уравнения системы (4) снизу вверх, мы получим выражения главных неизвестных через свободные - . Указанные выражения неизвестных через неизвестные называется общим решением системы (1).

Придавая свободным неизвестным произвольные числовые значения , вычислим соответствующие значения главных неизвестных. Пусть эти значения .

Очевидно, что упорядоченный набор является решением системы (3). Это решение называется частным решением.

Так как свободным неизвестным можно придать бесконечное множество значений, то и система (3) имеет бесконечное множество решений.

Следовательно, система (1), в случае имеет бесконечное множество решений.

Случай 3. Пусть матрица имеет вид

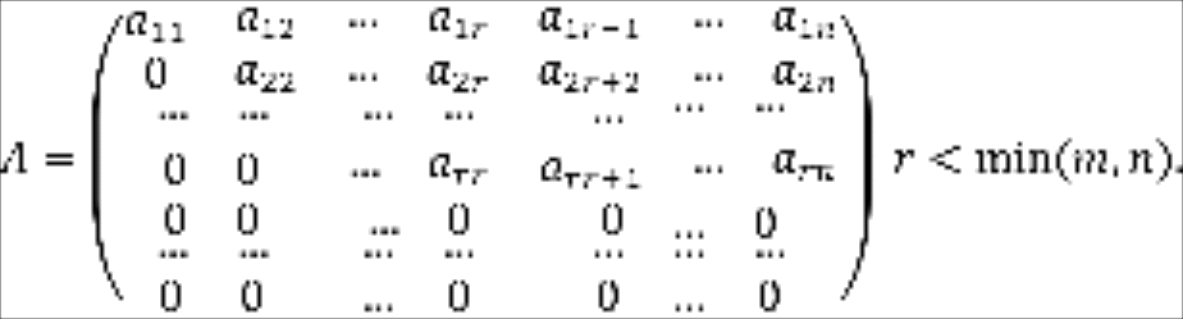
Тогда система (1) имеет следующий вид

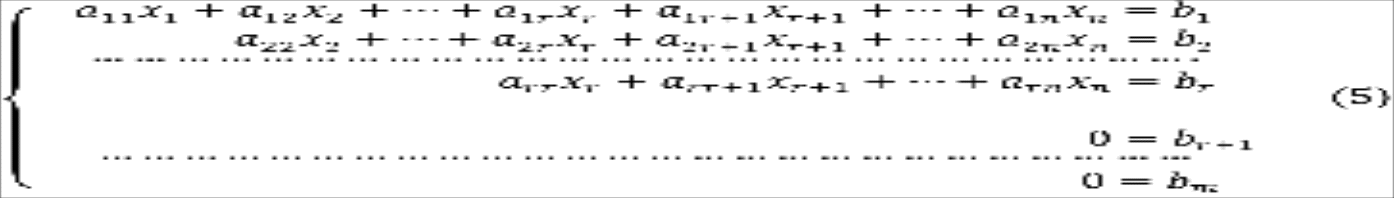
Докажем, что система (5) совместна тогда и только тогда, когда .

Доказательство. Пусть система (5) совместна. Тогда существуют такие значения неизвестных , при которых все уравнения системы превращаются в тождества. Следовательно . Пусть теперь выполнены равенства . Тогда система (5) имеет вид

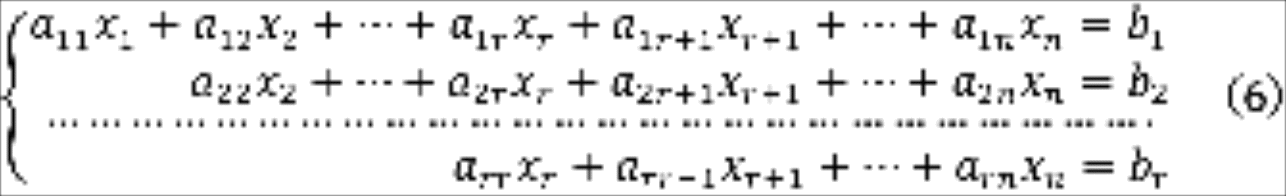
Система (6) называется укороченной системой. Очевидно, что, при выполнении равенств

системы (5) и (6) эквивалентны.

Основная матрица системы (6) имеет вид, рассмотренный в случае 2. Следовательно, система (6) имеет бесконечное множество решений, а стало быть, совместна.

Заметим, что в случае 3, при выполнении равенств , расширенная матрица

системы (5) является верхней трапециевидной матрицей, при этом

Таким образом, в случае , если среди коэффициентов хотя бы один не равен нулю, то система (5) несовместна. Если же все , то система (5) имеет бесконечное множество решений.

Случай 4. Пусть верхняя трапециевидная матрица имеет вид

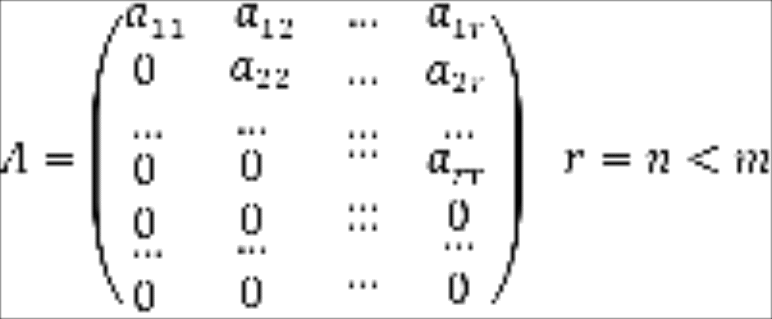
Тогда система (1) имеет вид

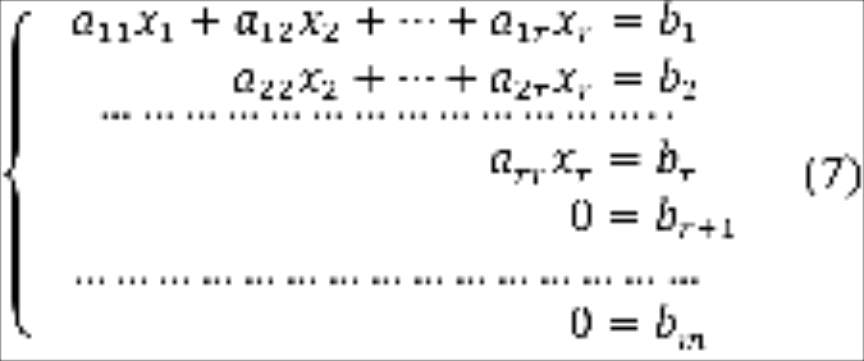
Из чего следует, что система (7) совместна тогда и только тогда, когда все . При этом, если все , то система (7) эквивалентна укороченной системе (2), описанной в случае 1, которая имеет единственное решение.

Заметим, что в случаях 3 и 4, равенство выполняется тогда и только тогда, когда . Следовательно, как и в случаях 1 и 2, система (1) совместна тогда и только тогда, когда

Из проведённых выше рассуждений следует, что система линейных алгебраических уравнений с верхней трапециевидной матрицей совместна тогда и только тогда, когда ранг основной матрицы При этом система либо имеет единственное решение ( , либо имеет бесконечное множество решений ( , либо не имеет ни одного решения (