4. Классификация точек разрыва.

Точка называется точкой разрыва функции , если функция в точке не является непрерывной.

Согласно определению непрерывной функции и теореме 4.1 функция непрерывна в точке тогда и только тогда, когда выполнены следующие условия:

1. Функция определена в некоторой окрестности точки ;

2. Должны существовать конечные пределы в точке справа и слева ;

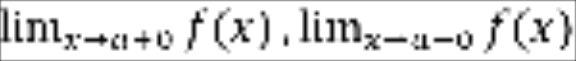3. Эти односторонние пределы должны быть равными;

4. Эти пределы должны быть равны .

Следовательно точка будет точкой разрыва функции , если нарушается, хотя бы одно из перечисленных условий.

В зависимости от того, какое из указанных условий нарушено, различают следующие виды точек разрыва.

Точка называется точкой устранимого разрыва функции , если существуют конечные односторонние пределы в точке , эти пределы равны, но не равны значению функции в точке , т.е.

Если функция имеет устранимый разрыв в точке , то для устранения этого разрыва достаточно изменить значение функции только в одной точке , положив его равным односторонним пределам в точке .

Точка называется точкой разрыва первого рода функции , если функция имеет в этой точке конечные, но не равные друг другу односторонние пределы.

Точка называется точкой разрыва второго рода функции , если хотя бы один из двух односторонних пределов функции в этой точке, либо не существует, либо является бесконечным.

Приведем несколько примеров.

Пример 1. функция

имеет в точке устранимый разрыв, так как

Пример 2. Функция

имеет в точке разрыв первого рода, так как

Пример 3. Функция имеет в точке разрыв второго рода, так как у этой функции не существует в точке 0 ни левого, ни правого пределов. Действительно, если бы существовал предел , то для любой последовательности . Возьмём две последовательности и , тогда , т.е. ,

. Следовательно, у функции в точке не существует правого предела.

Аналогично доказывается, что у этой функции не существует в точке 0 левого предела.

Пример 4. Функция имеет в точке разрыв второго рода, так как .

5. Основные свойства непрерывных функций.

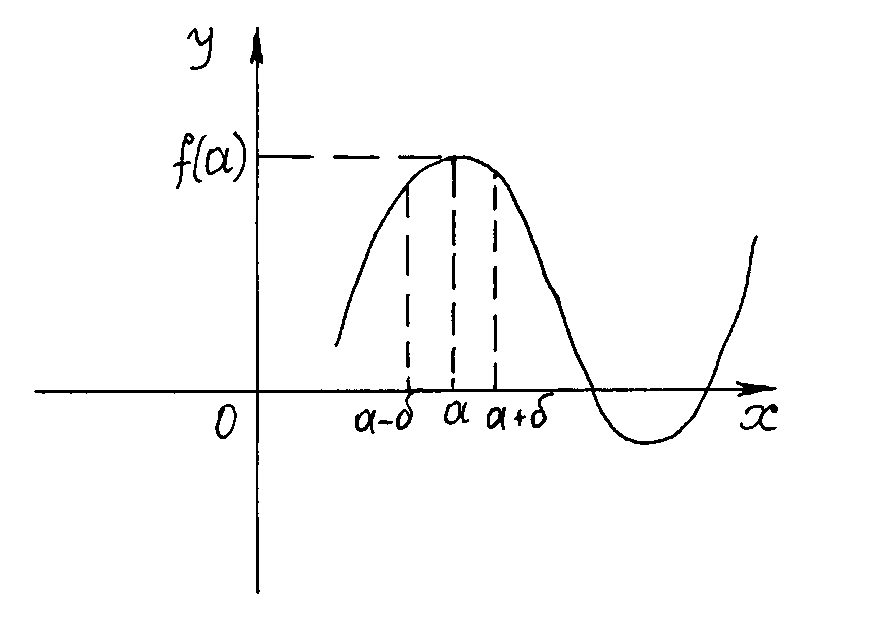
Теорема 5.2. (теорема об устойчивости знака непрерывной функции). Пусть функция непрерывна в точке и . Тогда существует такое, что всюду в пределах окрестности точки , функция имеет тот же знак, что .

Доказательство. Рассмотрим сначала случай . Так как функция непрерывна в точке , то для положительного числа существует положительное число такое, что для всех , удовлетворяющих неравенству будет выполнятся неравенство или

Из левого неравенства находим для всех , что и требовалось доказать.

Пусть теперь . Рассмотрим функцию . Тогда и согласно доказанному, существует такая – окрестность , что в каждой точке этой окрестности или . Теорема 5.2 доказана.

Аналогичная теорема справедлива и для функции, которая является непрерывной в точке только справа или только слева.

Для любого полусегмента будем называть правой -полуокрестностью точки , а полусегмент – левой -полуокрестностью точки .

Справедлива следующая теорема.

Теорема 5.2^’. Если функция определена в некоторой правой (левой) полуокрестности точки , непрерывна в точке справа (слева) и её значение отлично от нуля, то найдётся такое положительное число , что функция всюду в правой (левой) -полуокрестности точки имеет тот же знак, что и в точке .

Для доказательства этой теоремы нужно дословно повторить доказательство теоремы 5.2, при этом термин окрестность точки заменить на термин правая (левая) -полуокрестность точки .

Теорема 5.3. (О прохождении через нуль непрерывной на сегменте функции) Пусть функция непрерывна на сегменте и её значения на концах этого сегмента и являются числами разных знаков, тогда внутри сегмента найдётся такая точка , в которой .

Доказательство. Без ограничения общности можно считать, что .

Обозначим через . Очевидно, E непустое ограниченное множество, так как и В силу теоремы 2.1 §2 гл. 5 у множества существует точная верхняя грань . Заметим, что не может совпадать с концами сегмента . Действительно, если , то в силу теоремы 5.2 ^’ , существует правая -полуокрестность точки , такая, что для всех . Следовательно, существует точка , такая, что , чего быть не может. Аналогично, из свойств непрерывных функций и определения точной верхней грани, следует, что

Докажем, что . Действительно, если , то в силу теоремы 5.2 найдется -окрестность точки , в пределах которой будет иметь определенный знак, что невозможно, поскольку по определению точной верхней грани найдется хотя бы одно значение из полусегмента , для которого , а для любого значения из интервала справедливо неравенство . Теорема доказана.

Теорема 5.4. (прохождение непрерывной на сегменте функции через любое промежуточное значение) Пусть функция непрерывна на сегменте , причём . Тогда для любого значения , заключённого между числами и , на сегменте найдётся точка , такая что .

1. Если , то и в качестве можно взять точку или точку .

2. Если совпадает с или с , то в качестве можно взять или или соответственно.

3. . Без ограничения общности будем считать, что . Пусть - любое число, удовлетворяющее неравенству . Рассмотрим функцию . Очевидно, функция непрерывна на сегменте . Кроме этого и

. Тогда, согласно теореме 5.3 существует такая точка внутри сегмента, что , или . Теорема 5.4 доказана.

Теорема 5.5. (Первая теорема Вейерштрасса) Если функция непрерывна на отрезке , то она ограничена на этом сегменте.

Доказательство. Приведём доказательство только ограниченности сверху, ибо ограниченность снизу доказывается аналогично.

Доказательство проведем от противного. Предположим, что функция непрерывна на отрезке и не ограничена на этом сегменте.

Для каждого натурального рассмотрим множество . По предположению, функция не ограничена, поэтому для каждого натурального ,

Отметим следующие два свойства множества :

1. Для любого множество является ограниченным.

2. Для любого

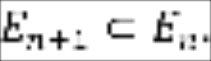
Действительно, ограниченность множеств вытекает из очевидного включения

Если , то . Следовательно , поэтому и

Итак, мы имеем последовательность непустых, ограниченных множеств . Из теоремы 2.1 §2 главы 5 следует, что для любого у множества существует точная нижняя грань .

Рассмотрим последовательность , элементы которой определяются равенством (3).

Докажем, что последовательность удовлетворяет следующим трём условиям:

1. Последовательность ограничена сверху;

2. Последовательность является неубывающей последовательностью;

3. .

Ограниченность сверху последовательности следует из того факта, что для любого Из этого включения следует, что число является верхней гранью множеств , но тогда

Докажем, что для любого справедливо неравенство . Действительно, поэтому для каждого справедливо неравенство Тогда из доказанного выше, вложения следует, что для каждого , т.е. является одной из нижних граней множества но тогда , т.к. - точная нижняя грань множества является наибольшей среди всех нижних граней множества .

Докажем теперь, справедливость условия 3. Предположим обратное, т.е. пусть при некотором

. (4)

Заметим, что точка не может совпадать с правым концом сегмента , так как, если , то и Это означает, что множество состоит из единственной точки Но тогда, в силу вложения , все множества , начиная с номера состоят из единственной точки . Тогда, в силу определения множества , для всех номеров ,верно неравенство Чего быть не может. Итак

Рассмотрим функцию . Очевидно, функция непрерывна на сегменте и при этом, в силу неравенства (4), . В силу теоремы 5.2, существует такая правая полуокрестность точки , всюду в пределах которой что невозможно, так как, по определению точной нижней грани, в полуокрестности найдется точка , для которой .

Итак, мы имеем неубывающую, ограниченную сверху последовательность . В силу теоремы 3.10 (о сходимости монотонной ограниченной последовательности) последовательность сходится к некоторой точке сегмента Тогда, в силу непрерывности функции в точке , сходится и последовательность , что невозможно, так как Теорема доказана.

Заметим, что все условия теоремы 5.5 существенны.

В качестве примера рассмотрим функцию непрерывную на интервале

Очевидно, эта функция неограниченна на Т.е. из непрерывности функции на интервале, не следует её ограниченность на этом интервале.

Из теоремы 5.5 следует, что множество значений функции является ограниченным множеством. Поэтому по теореме 2.1 §2 главы 5 у этого множества существуют точная верхняя грань и точная нижняя грань . Числа и называются соответственно точной верхней и точной нижней гранями функции на сегменте и обозначаются символами , .

Естественно возникает вопрос: являются ли для функции , непрерывной на сегменте эти точные грани достижимыми, т.е. существуют ли точки и , принадлежащие сегменту , такие, что и . На этот вопрос даёт ответ следующая теорема.

Теорема 5.6. (Вторая теорема Вейерштрасса). Если функция непрерывна на сегменте , то она достигает на этом сегменте своих точных граней, т.е. существуют точки , сегмента такие, что

Доказательство. Т.к. функция непрерывна на сегменте , то по теореме 5.5 она ограничена на этом сегменте, т.е. множество является ограниченным. Пусть

. Покажем, что существует точка такая, что . Предположим обратное, пусть для каждого , Тогда в каждой точке . Рассмотрим на сегменте функцию . По теореме 5.1 §5 главы 5 функция непрерывна на . Из теоремы 5.5 следует ограниченность функции на сегменте , т.е. существует , такое что но тогда для любого . Таким образом, число является верхней гранью функции на сегменте . Но это, противоречит тому, что число является точной верхней, т.е. наименьшей верхней гранью функции на отрезке .

Аналогично доказывается существование точки в которой функция достигает значения Теорема 5.6 доказана