Глава 7. Теоремы о дифференцируемых функциях и их приложения

§1 Локальный экстремум функции.

1. Теорема Ферма. (Необходимое условие локального экстремума).

Определение 1.1. Точка называется точкой локального максимума (минимума) функции , если существует такая окрестность точки , что для любой точке справедливо неравенство .

Если в определении 1.1 вместо неравенства требовать выполнение неравенства , то такая точка называется точкой строгого локального максимума (минимума) функции .

Определение 1.1. (Теорема Ферма о необходимом условии локального экстремума).

Пусть функция определена на интервале и пусть в точке локальный экстремум. Тогда если дифференцируема в , то .

Если функция дифференцируема в точке и имеет в этой точке локальный экстремум, то .

Доказательство. Рассмотрим случай, когда функция имеет в точке локальный максимум. Тогда существует такая окрестность точки , что , т.е.

Т.к. функция дифференцируема в точке , то существуют правая и левая производные в точке , при этом

По определению правой производной

Т.к. , то , следовательно, из неравенства (1) имеем . Тогда такому неравенству удовлетворяет , т.е. . Рассмотрим теперь . Т.к. , то , тогда из неравенства (1) следует . Следовательно

Итак, мы доказали, что и , что возможно только в случае .

Аналогично рассматривается случай локального минимума.

Теорема 1.1 доказана.

Теорема 1.1 имеет простой геометрический смысл: если дифференцируемая в точке функция имеет в этой точке локальный экстремум, тогда касательная проведённая к графику функции в точке параллельна оси .

2. Теорема Ролля.

Теорема 1.2. Если функция непрерывна на сегменте и имеет производную во всех точках интервала , кроме того , то внутри сегмента найдётся такая точка , производная в которой равна нулю.

Доказательство. Так как функция непрерывна на сегменте , то по второй теореме Вейерштрасса она достигает на сегменте своих наибольшего и наименьшего значений. Т.е. существуют такие точки , что . При этом

Возможны два случая: 1.

В первом случае . Поэтому производная функции равна нулю в любой точке , т.е. для этого случая теорема доказана.

Во втором случае, т.к. , то хотя бы одно из двух значений или не принимается на концах сегмента , т.е. существует такая точка , в которой функция принимает наибольшее или наименьшее значение на интервале . Тогда по теореме 1.1 (теорема Ферма) . Теорема 1.2 доказана.

Теорема Ролля имеет простой геометрический смысл: если для непрерывной на сегменте и дифференцируемой на интервале функции, то на графике функции существует точка , в которой касательная к графику параллельна .

3. Теорема Лагранжа.

Теорема 1.3. Если функция непрерывна на сегменте и дифференцируема в каждой точке интервала , то существует такая точка , что

Формула (4) называется формулой Лагранжа.

Доказательство. Рассмотрим функцию , определённую на сегменте . Заметим, что для функции выполнены все условия теоремы Ролля. Действительно, функция непрерывна как разность непрерывных функций и . Функция дифференцируема в каждой точке интервала как разность указанных дифференцируемых на интервале функций. И, наконец, и

, т.е. . Тогда по теореме Ролля существует точка , такая, что . Вычислим .

Из равенства (6) следует, что или

Теорема доказана.

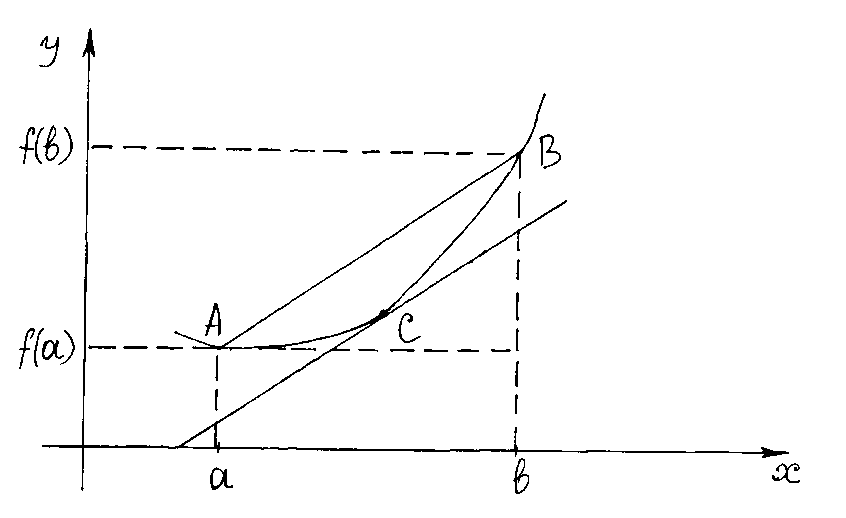
Теорема Лагранжа также имеет простой геометрический смысл. Прежде всего заметим, что величина является угловым коэффициентом секущей, проходящей через точки и кривой , а является угловым коэффициентом касательной, проведённой к графику функции в точке . В теореме Лагранжа утверждается, что между точками и найдётся точка , касательная в которой параллельна секущей .

Теорема 1.4. Если функция дифференцируема в каждой точке интервала и если в каждой точке указанного интервала , то функция является постоянной на интервале .

Доказательство. Рассмотрим произвольные две точки и интервала . Тогда , поэтому функция дифференцируема, а стало быть и непрерывна на сегменте . Тогда по теореме Лагранжа , где . Т.к. , то получим . Т.е. значения функции в произвольных точках и совпадают, т.е.

. Теорема доказана.

Теорема 1.4 имеет простой геометрический смысл: если касательная к графику функции проведённая в любой точке , где параллельна оси , то график функции представляет собой отрезок прямой, параллельной .