
- •Глава 1. Матрицы
- •§1 Понятие матрицы
- •§2. Операции над матрицами
- •§3 Элементарные преобразования матриц
- •§4. Определители
- •§5. Обратная матрица
- •§6. Ранг матрицы.
- •Глава 2. Системы линейных алгебраических уравнений.
- •§1. Постановка задачи. Терминология.
- •§2 Системы с квадратной невырожденной матрицей.
- •§3. Элементарные преобразования системы линейных алгебраических уравнений.
- •§4. Системы с верхней трапециевидной матрицей.
- •§5.Системы общего вида
- •§6. Однородные системы линейных алгебраических уравнений.
- •Глава 3. Векторная алгебра.
- •§1. Декартовы координаты на прямой.
- •§2. Декартовы прямоугольные координаты на плоскости и в пространстве.
- •§3. Понятие вектора и линейные операции над векторами.
- •§4. Проекция вектора на ось и её свойства.
- •§5. Скалярное произведение двух векторов.
- •Глава 4. Основы аналитической геометрии
- •§1. Простейшие задачи аналитической геометрии.
- •1. Расстояние между двумя точками
- •2. Деление отрезка в данном отношении.
- •Полярная система координат.
- •§2. Различные виды уравнений прямой на координатной плоскости. Взаимное расположение прямых.
- •1. Параметрические уравнения прямой.
- •2. Каноническое уравнение прямой в плоскости.
- •3. Общее уравнение прямой в плоскости.
- •4. Уравнение прямой в отрезках.
- •5. Неполные уравнения прямой.
- •6. Уравнение прямой, проходящей через заданные две точки.
- •7. Уравнение прямой с угловым коэффициентом.
- •8. Условия пересечения, коллинеарности и ортогональности двух прямых. Угол между двумя пересекающимися прямыми.
- •9. Пучок прямых, уравнение пучка прямых.
- •10. Нормированное уравнение прямой. Расстояние от точки до прямой.
- •§3. Кривые второго порядка.
- •Эллипс. Каноническое уравнение эллипса.
- •2. Гипербола.
- •3. Парабола.
- •4. Линейные преобразования декартовых прямоугольных координат.
- •Глава 5. Элементы математического анализа
- •§1. Множества. Операции над множествами.
- •§2. Вещественные числа и их основные свойства
- •1. Рациональные числа и их основные свойства.
- •2. Вещественные числа и правило их сравнения.
- •3. Множества вещественных чисел, ограниченные сверху или снизу.
- •4. Операция сложения и умножения вещественных чисел.
- •§ 3. Числовые последовательности.
- •1. Понятие последовательности. Арифметические операции над последовательностями.
- •2. Ограниченные, неограниченные, бесконечно большие и бесконечно малые последовательности.
- •3. Сходящиеся последовательности и их свойства.
- •4. Монотонные последовательности.
- •§4. Функция и её предел.
- •Односторонние пределы.
- •4. Предел функции при и при .
- •5. Арифметические операции над функциями, имеющими предел.
- •6. Бесконечно малые и бесконечно большие функции.
- •7. Замечательные пределы.
- •§5. Непрерывные функции.
- •2. Арифметические операции над непрерывными функциями.
- •3. Примеры непрерывных функций.
- •4. Классификация точек разрыва.
- •5. Основные свойства непрерывных функций.
- •6. Понятие сложной функции.
- •7. Понятие обратной функции.
- •Глава 6. Основы дифференциального исчисления.
- •§1. Производная.
- •1. Приращение аргумента и функции. Разностная форма условия непрерывности.
- •2. Определение производной.
- •3. Геометрический смысл производной.
- •4. Физический смысл производной.
- •5. Правая и левая производные.
- •6. Понятие дифференцируемости функции.
- •7. Понятие дифференциала функции.
- •§2. Дифференцирование сложной функции и обратной функции.
- •1. Дифференцируемость сложной функции.
- •2. Дифференцируемость обратной функции.
- •3. Инвариантность формы первого дифференциала.
- •§3. Дифференцирование суммы, разности, произведения и частного функции.
- •§4. Производные простейших элементарных функций.
- •12. Таблица производных простейших элементарных функций.
- •13. Таблица дифференциалов простейших элементарных функций.
- •13. Логарифмическая производная степенно-показательной функции.
- •§5. Производные и дифференциалы высших порядков.
- •1. Понятие производной -го порядка.
- •3. Формула Лейбница для -й производной произведения двух функций.
- •4. Дифференциалы высших порядков.
- •Глава 7. Теоремы о дифференцируемых функциях и их приложения
- •§1 Локальный экстремум функции.
- •2. Теорема Ролля.
- •3. Теорема Лагранжа.
- •4. Достаточное условие монотонности функции на интервале.
- •5. Формула Коши.
- •§2. Раскрытие неопределённостей (правило Лопиталя)
- •1. Первое правило Лопиталя.
- •2. Второе правило Лопиталя.
- •3. Другие виды неопределённостей и их раскрытие.
- •§3. Формула Тейлора
- •1. Формула Тейлора с остаточным членом в форме Лагранжа.
- •2. Другая запись формулы Тейлора и остаточного члена в форме Пеано.
- •3. Формула Маклорена.
- •4. Разложение некоторых элементарных функций по формуле Маклорена.
- •§4. Достаточное условие экстремума.
- •1. Первое достаточное условие экстремума.
- •2. Второе достаточное условие экстремума.
- •3. Экстремум функции, не дифференцируемой в данной точке.
- •§5. Направление выпуклости графика функции. Точки перегиба.
- •1. Направление выпуклости графика функции.
- •2. Точки перегиба графика функции.
- •§6. Асимптоты графика функции.
- •Глава 8. Неопределённый интеграл.
- •§1. Понятие первообразной функции и неопределённого интеграла.
- •1. Понятие первообразной функции.
- •2. Неопределённый интеграл.
- •3. Основные свойства неопределённого интеграла.
- •4. Таблица основных интегралов.
- •§2. Основные методы интегрирования.
- •1. Интегрирование заменой переменной.
- •2. Метод интегрирования по частям.
- •Глава 9. Определённый интеграл.
- •§1. Понятие определённого интеграла.
- •1. Интегральная сумма и её предел.
- •2. Верхние и нижние суммы.
- •§2. Свойства определённого интеграла.
- •§3. Существование первообразной у любой непрерывной функции.
- •§4. Основная формула интегрального исчисления.
- •1. Формула Ньютона-Лейбница.
- •2. Замена переменной в определённом интеграле.
- •3. Формула интегрирования по частям в определённом интеграле.
- •§5. Несобственные интегралы.
- •1. Несобственный интеграл первого рода.
- •2. Несобственный интеграл II рода.
- •§6. Геометрические и физические приложения определённого интеграла.
- •1. Площадь криволинейной трапеции.
- •2. Площадь криволинейного сектора.
- •3. Длина дуги плоской кривой.
- •5. Площадь поверхности вращения.
- •6. Физические приложения определённого интеграла.
§3. Кривые второго порядка.
Эллипс. Каноническое уравнение эллипса.
Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.
Обозначим фокусы
эллипса через ![]() и
и ![]() ,
расстояние между фокусами
,
расстояние между фокусами ![]() через
через ![]() ,
сумму расстояний от произвольной точки
эллипса до фокусов через
,
сумму расстояний от произвольной точки
эллипса до фокусов через ![]() .
Тогда по определению
.
Тогда по определению ![]() ,
т.е.
,
т.е. ![]() .
.
Введём прямоугольную
систему координат так, чтобы фокусы
эллипса лежали на оси абсцисс, а начало
координат находилось в середине отрезка
![]() .
Тогда фокусы имеют координаты
.
Тогда фокусы имеют координаты ![]() ,
,
![]() .
.
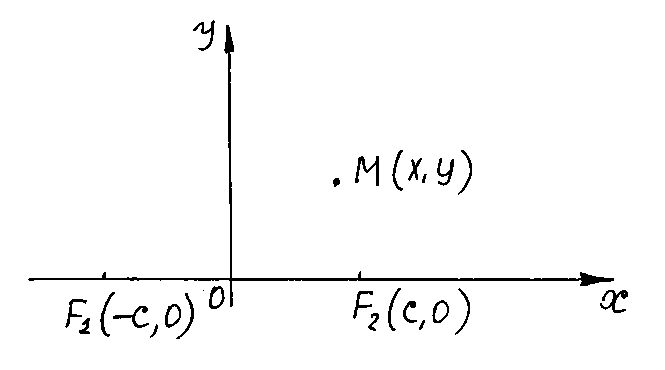
Пусть
– произвольная точка плоскости, ![]() и
и ![]() -
расстояния от точки
до фокусов
и
соответственно. Числа
и
называются фокальными радиусами точки
.
Очевидно, что точка
будет лежать на данном эллипсе тогда и
только тогда, когда
-
расстояния от точки
до фокусов
и
соответственно. Числа
и
называются фокальными радиусами точки
.
Очевидно, что точка
будет лежать на данном эллипсе тогда и
только тогда, когда ![]() .
.
Найдём расстояния и .
![]()
Подставляя эти выражения в равенство (1), получим
![]()
Перенесём второй радикал в правую часть уравнения, а затем возведём обе части в квадрат
![]()
![]()
![]()
Возведём снова в квадрат обе части уравнения (4)
![]()
![]()
Обозначим ![]() через
,
тогда из уравнения (5) получим
через
,
тогда из уравнения (5) получим
![]()
Разделив обе части
на ![]() ,
получим
,
получим
![]()
Уравнение (7) получено из уравнения (3), поэтому координаты любой точки, удовлетворяющие уравнению (3) , будут удовлетворять и уравнению (7). Однако при упрощении уравнения (3) обе его части дважды возводили в квадрат, следовательно, могли появиться такие точки, координаты которых удовлетворяют уравнению (7), но не удовлетворяют уравнению (3).
Убедимся в том, что если координаты некоторой точки удовлетворяют уравнению (7), то они удовлетворяют и уравнению (3), что будет означать равносильность уравнений (3) и (7) .
Пусть – произвольная точка плоскости, координаты которой удовлетворяют уравнению (7).
![]()
Рассмотрим фокальный
радиус точки ![]() -
- ![]()


![]()
Из уравнения (7) имеем.
![]()
Непосредственно из определения эллипса следует неравенство
![]() (10)
(10)
Из неравенств (9) и (10) следует, что
![]()
поэтому
![]()
Аналогично доказывается, что
![]()
Складывая
и
,
получим ![]() .
Т.е. получаем равенство (1). Из равенства
(1) в свою очередь следует справедливость
равенства (3). Таким образом, любая точка,
координаты которой удовлетворяют
уравнению (7), принадлежит эллипсу.
.
Т.е. получаем равенство (1). Из равенства
(1) в свою очередь следует справедливость
равенства (3). Таким образом, любая точка,
координаты которой удовлетворяют
уравнению (7), принадлежит эллипсу.
Уравнение (7) называется каноническим уравнением эллипса.
Заметим, что
уравнение (7) содержит только члены с
чётными степенями
и ![]() ,
поэтому эллипс симметричен относительно
осей
и
,
а также относительно начала координат.
Таким образом, можно знать форму эллипса,
если установить вид той его части,
которая находится в первом координатном
угле.
,
поэтому эллипс симметричен относительно
осей
и
,
а также относительно начала координат.
Таким образом, можно знать форму эллипса,
если установить вид той его части,
которая находится в первом координатном
угле.
Из уравнения (7)
имеем ![]() .
.
Так как в первом
координатном угле ![]() ,
то из равенства (11) имеем
,
то из равенства (11) имеем

Из последнего равенства вытекает:
Если
 ,
то
,
то  ,
т.е. точка
,
т.е. точка  лежит на эллипсе.
лежит на эллипсе.
При возрастании от 0 до
 уменьшается.
уменьшается.
Если
 ,
то
,
то  ,
т.е. точка
,
т.е. точка  лежит на эллипсе.
лежит на эллипсе.
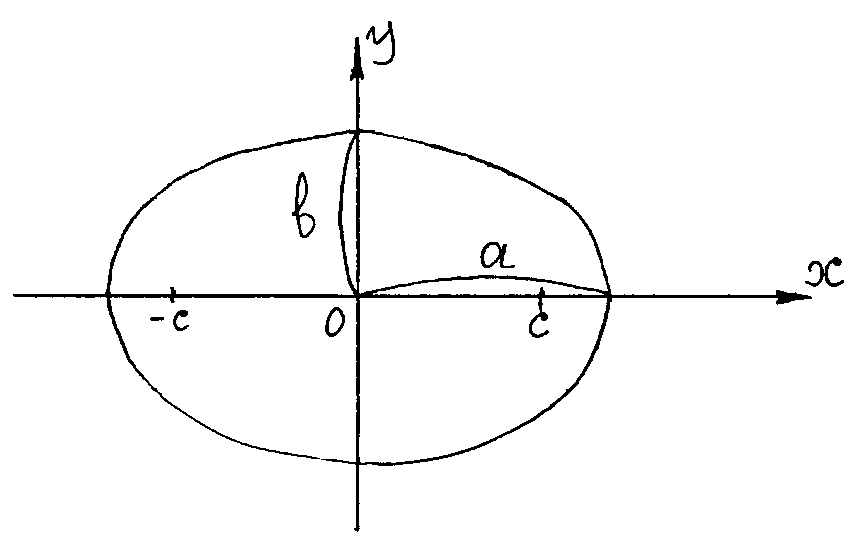
и в уравнении эллипса называются большой и малой полуосями.
Точки, в которых эллипс пересекает оси, называются его вершинами.
Заметим, что если
![]() ,
то уравнение (7) принимает вид
,
то уравнение (7) принимает вид ![]() .
Это уравнение окружности радиуса
с центром в точке
.
Это уравнение окружности радиуса
с центром в точке ![]() .
Т.е. окружность – частный случай эллипса.
.
Т.е. окружность – частный случай эллипса.
Эксцентриситетом
эллипса называется отношение ![]() ,
где
,
где ![]() - половина расстояния между фокусами,
- большая полуось эллипса.
- половина расстояния между фокусами,
- большая полуось эллипса.
Эксцентриситет
обычно обозначают буквой ![]() .
Т.к.
.
Т.к. ![]() ,
то
,
то ![]() .
.
Принимая во
внимание, что ![]() ,
найдём
,
найдём ![]() ,
откуда
,
откуда ![]() .
.
Из последнего равенство легко получается геометрическая иллюстрация эксцентриситета эллипса. При малых значениях 𝜀 числа и почти равны, т.е. эллипс близок к окружности. Если же 𝜀 близко к единице, то число весьма мало по сравнению с числом , т.е. эллипс сильно вытянут вдоль большой оси. Таким образом, эксцентриситет эллипса характеризует меру вытянутости.
Известно, что планеты и некоторые кометы движутся по эллиптическим траекториям. Оказывается, планеты движутся почти по окружностям, т.е. эксцентриситеты их орбит близки к нулю, а для орбит комет наоборот, эксцентриситет близок к единице. При этом в одном из фокусов находится солнце. Т.е. некоторые кометы то «сильно» приближаются к солнцу, то сильно удаляются от него.
