§3 Элементарные преобразования матриц

Приведение матрицы к верхней трапециевидной форме.

Элементарными преобразованиями матрицы называются преобразования следующих трёх типов:

1. Перестановка двух строк (столбцов) матрицы;

2. Умножение строки (столбца) на число отличное от нуля;

3. Прибавление к одной строке (столбцу) матрицы другой её строки (столбца), умноженной на любое число

Теорема 3.1. (об основном процессе)Произвольная ненулевая матрица конечным числом элементарных преобразований строк и перестановками столбцов может быть приведена к верхней трапециевидной форме

Доказательство Пусть . Процесс приведения ненулевой матрицы к верхней трапециевидной форме состоит в общем случае из шагов. Иногда этот процесс заканчивается раньше, давая нужный результат.

Первый шаг. а) Так как , то в матрице существует элемент . Если , то переходим к пункту «б». Если , то, поменяв в матрице местами 1-ю и -ю строки, а затем, в полученной матрице поменяв местами 1-й и -й столбцы, получим матрицу , в которой элемент в позиции (1, 1) - = .

б) Элемент назовём ведущим элементом первого шага. С его помощью аннулируем все расположенные под ним элементы 1-го столбца. Для этого из каждой строки, начиная со второй, вычтем первую строку, умноженную на , , …, соответственно.

После выполнения первого шага матрица переходит в матрицу

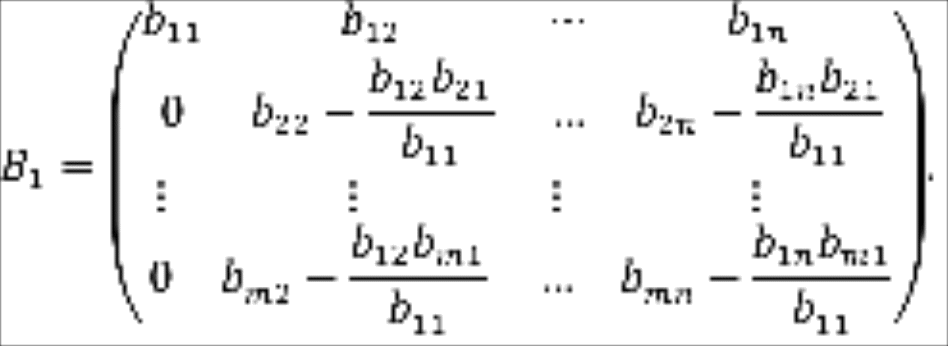
Если при этом все строки, начиная со второй, стали нулевыми, то весь процесс завершается, так как матрица уже приведена к верхней трапециевидной форме. Если же в этих строках есть хотя бы один, отличный от нуля элемент, т.е. если матрица

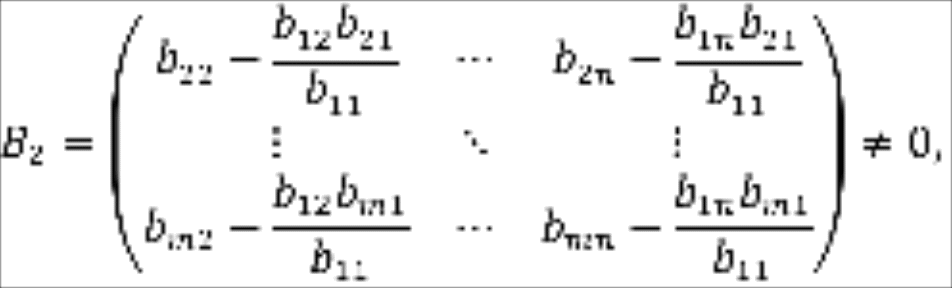
то переходим ко второму шагу.

Второй шаг. Второй шаг аналогичен первому, он состоит в применении к матрице преобразований, описанных в первом шаге. При этом можно считать, что выполняются элементарные преобразования строк всей матрицы , так как все элементы первого столбца матрицы , начиная со второго, равны нулю.

Повторяя описанные преобразования на следующих шагах, самое большое через шагов мы получим требуемый результат.

Заметим, что, если описанный процесс приведения матрицы к верхней трапециевидной форме, применить к квадратной матрице, то в результате получится верхняя треугольная матрица.

§4. Определители

Понятие определителя квадратной матрицы , для .

Определитель – это некоторое число поставленное в соответствие квадратной матрице .

Для неквадратных матриц понятие определителя не вводится.

Для обозначения определителя квадратной матрицы A будем пользоваться обозначением или .

Пусть - произвольная квадратная матрица порядка . Если , то матрица состоит из одного числа . Положим по определению, что определитель такой матрицы равен числу , т.е. . Если , то матрица имеет вид

Положим по определению, что определитель такой матрицы равен

Если , то матрица имеет вид

Положим по определению, что определитель такой матрицы равен

Для облегчения запоминания равенств (1) и (2), приведём удобные мнемонические правила, дающие схему вычисления положительных и отрицательных членов определителей второго и третьего порядков соответственно.

+ -

+ -

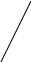
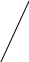
В этих схемах элементы, входящие в одно произведение, соединены отрезками

Основные свойства определителей.

Свойство 1. Определитель квадратной матрицы не изменяется при её транспонировании: .

Доказательство свойства 1 для квадратных матриц 2 и 3 порядков проводится по единой схеме. Приведём доказательство для квадратной матрицы 2-го порядка.

Пусть

Свойство 2. Если одна из строк (столбцов) матрицы целиком состоит из нулей, то её определитель равен нулю.

Свойство 2 непосредственно вытекает из определения определителя.

Свойство 3. При перестановке местами любых двух строк (столбцов) матрицы её определитель меняет знак.

Доказательство свойства 3 приведём для квадратных матриц третьего порядка. Пусть

Пусть - матрица, полученная из матрицы перестановкой мест первых двух строк, т.е.

Аналогично проходит доказательство свойства 3, при перестановке любых других строк (столбцов).

Свойство 4. При умножении строки (столбца) матрицы на число её определитель умножается на это число.

Доказательство свойства 4 приведём для случая умножения элементов первой строки, квадратной матрицы третьего порядка, на произвольное число .

Пусть

Аналогично доказывается свойство 4 для всех остальных случаев.

Свойство 5. Если каждый элемент i-й строки (столбца) матрицы представлен в виде суммы двух слагаемых, то определитель такой матрицы равен , где элементы матриц и , за исключением элементов -й строки (столбца), совпадают с соответствующими элементами матрицы . А в -х строках (столбцах) матриц и стоят упомянутые первые и вторые слагаемые соответственно.

Доказательство свойства 5 приведём для случая, когда элементы первой строки квадратной матрицы второго порядка, представлены в виде двух слагаемых.

Пусть .

Аналогично доказывается свойство 5 и для квадратных матриц третьего порядка.

Отметим некоторые следствия, непосредственно вытекающие из перечисленных 5 основных свойств определителя.

Следствие 1. Определитель матрицы, имеющей две одинаковые строки (столбца) равен нулю.

Доказательство. Пусть - квадратная матрица, имеющая две одинаковые строки (столбца). - матрица полученная в результате перестановки указанных одинаковых строк (столбцов) матрицы . Тогда, с одной стороны, , с другой стороны, в силу свойства 3, . Следовательно, . Из последнего равенства следует, что .

Следствие 2. Если какие-либо две строки (столбца) матрицы пропорциональны, то её определитель равен нулю.

Доказательство. Пусть - квадратная матрица третьего порядка, имеющая две пропорциональные строки.

Будем считать, без ограничения общности, что в матрице пропорциональны две строки. Предположим, что элементы второй строки получены умножением соответствующих элементов первой строки на некоторое число .

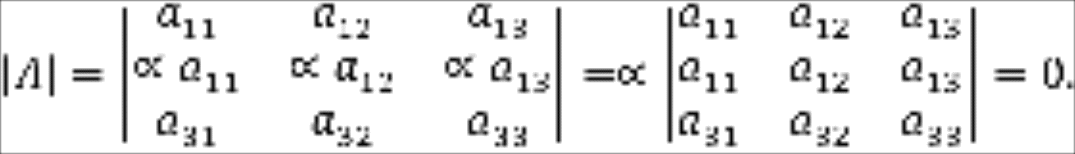
Следствие 3. Если к элементам какой-либо строки (столбца) прибавить соответствующие элементы любой другой строки (столбца), умноженные на любое число , то определитель не изменится.

Доказательство. Пусть - квадратная матрица третьего порядка

В качестве иллюстрации доказательства, рассмотрим случай, когда к элементам первой строки матрицы прибавляются элементы второй строки, умноженные на произвольное число . Тогда, в силу свойства 5 и следствия 2

=

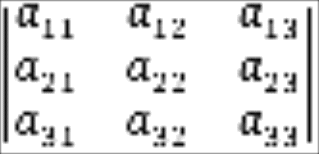
Миноры и алгебраические дополнения. Пусть - произвольная квадратная матрица, – её элемент, стоящий в позиции . Вычеркивая из матрицы i-ю строку и -ый столбец, получим некоторую матрицу , порядка . Определитель матрицы называется минором элемента . Минор элемента будем обозначать символом .

Число называется алгебраическим дополнением элемента . Для обозначения алгебраического дополнения элемента будем пользоваться символом .

Разложение определителя по строке (столбцу)

Теорема 4.1. Определитель квадратной матрицы равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения.

В качестве иллюстрации докажем, что определитель любой квадратной матрицы третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения. Пусть.

Рассмотрим сумму произведений элементов первой строки на их алгебраическое дополнение

Легко заметить, что правая часть равенства (3) равна определителю матрицы .

Понятие определителя квадратной матрицы любого порядка .

Приведённая теорема 4.1 может быть положена в основу последовательного введения по индукции определителя четвёртого, пятого и всех последующих порядков.

Предположим, что уже введено понятие определителя -го порядка. Пусть Минором каждого элемента матрицы является определитель -го порядка.

Назовём определителем квадратной матрицы число равное

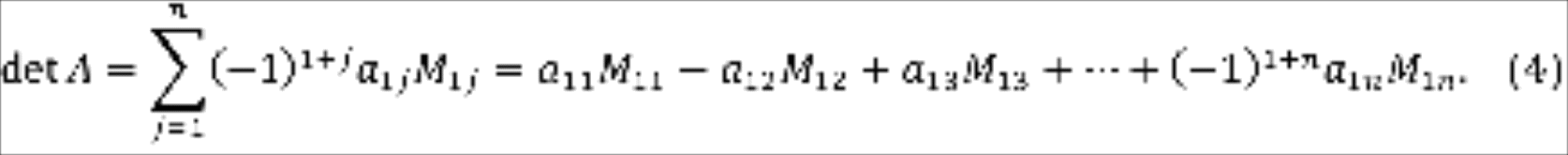
Заметим, что в правой части равенства (4) стоит сумма произведений элементов первой строки на их алгебраические дополнения.

Можно доказать, если взять сумму произведений элементов любой другой строки (столбца) матрицы на их алгебраические дополнения, то получится число, равное .

Заметим также, что при разложение (4) совпадает с разложением определителя третьего порядка по первой строке.

Такая схема введения определителя любого порядка изложена в книге В.А. Ильин, Э.Г. Позняк «Линейная алгебра» (М: Физматлит, 2001). Там же доказано, что определители любого порядка обладают теми же свойствами, что определители второго и третьего порядков.

Заметим, что теоретически, определитель любой квадратной матрицы порядка может быть вычислен с применением равенства (4). Однако на практике, при достаточно больших , применение равенства 4 весьма затруднительно, т.к. связано с большим числом вычислений. Так например, чтобы вычислить определитель 5-го порядка, надо вычислить 5 определителей четвёртого порядка или 20 определителей третьего порядка.

В дальнейшем приведём метод Гаусса, существенно облегчающий вычисление определителя.

Теорема 4.2. Определитель любой верхней треугольной (нижней треугольной) матрицы равен произведению диагональных элементов.

Доказательство. Рассмотрим случай верхней треугольной матрицы (Случай нижней треугольной матрицы рассматривается аналогично).

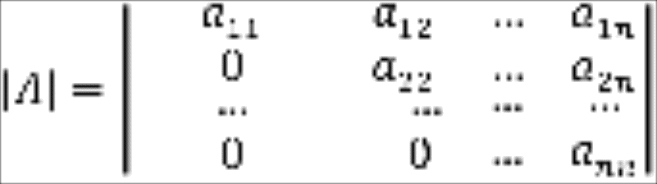
Разложив определитель по первому столбцу, получим

Раскладывая полученный определитель -го порядка по первому столбцу и продолжая этот процесс, мы получим, что

Теорема 4.2. доказана.

Следствие из теоремы 4.2. Определитель любой диагональной матрицы равен произведению диагональных элементов.

Данное следствие непосредственно вытекает из теоремы 4.2. и того факта, что любая диагональная матрица является как верхней треугольной, так и нижней треугольной.

Теорема 4.3. ^** Определитель произведения квадратных матриц и равен произведению определителей матриц-сомножителей, т.е.

Изящное доказательство этой теоремы можно найти в книге В.А. Ильин, Г.Д. Ким «Линейная алгебра и аналитическая геометрия».

Теорема 4.4. (О фальшивом разложении определителя). Сумма произведений элементов одной строки (столбца) квадратной матрицы, на алгебраические дополнения элементов другой её строки (столбца) равна нулю.

Доказательство. Пусть - произвольная квадратная матрица

Рассмотрим матрицу , которая отличается от только j-й строкой: на месте j-й строки в матрице стоит -я строка матрицы , т.е.

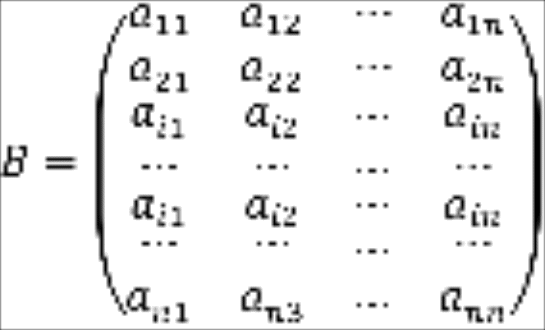
Определитель матрицы , т.к. в этой матрице две одинаковые строки. С другой стороны, по теореме 4.1. определитель матрицы равен сумме произведений элементов j-й строки на их алгебраические дополнения

Вычисление определителя. Во многих задачах линейной алгебры возникает необходимость вычисления определителя.

Среди различных методов вычисления определителя особое место занимает метод Гаусса.

Суть метода Гаусса вычисления определителя состоит в следующем:

1. Привести элементарными преобразованиями данную квадратную матрицу к треугольному виду. При этом такие преобразования либо не изменяют определителя матрицы, либо изменяют его контролируемым образом;

2. Вычислить определитель треугольной матрицы;

3. Восстановить исходный определитель.