
- •Предисловие
- •Оглавление
- •Сопротивление материалов – наука о прочности конструкций
- •Глава 1. Основные определения и допущения
- •1.1. Общие принципы расчета на прочность
- •1.2 Понятие о расчетной схеме
- •1.3 Формы тел, рассматриваемые в сопротивлении материалов
- •1.4 Классификация внешних сил
- •1.5 Опорные устройства и их реакции
- •1.6. Основные допущения о свойствах материалов и допущения, связанные с характером деформаций
- •Глава 2. Внутренние силы в поперечных сечениях бруса
- •Раздел 1. Метод сечений
- •1.1. Внутренние силовые факторы
- •Раздел 2. Центральное растяжение-сжатие. Нормальные силы
- •2.1. Нормальные усилия в стержнях стержневой системы
- •2.1.1. Нормальные усилия в стержнях статически определимой системы
- •2.1.2. Нормальные усилия в стержнях статически неопределимой стержневой системы
- •2.1.3 Температурные усилия в стержнях статически неопределимой стержневой системы
- •2.2. Центральное растяжение и сжатие ступенчатого бруса
- •2.2.1. Нормальные усилия возникающие при растяжении и сжатии статически определимого ступенчатого бруса
- •2.2.2. Нормальные усилия, возникающие при растяжении и сжатии статически неопределимого ступенчатого бруса
- •2.2.3 Эпюры нормальных сил при растяжении и сжатии ступенчатого бруса
- •Раздел 3. Кручение. Крутящие моменты
- •3.1. Крутящие моменты, возникающие при кручении статически определимого бруса
- •3.2. Крутящие моменты, возникающие при кручении статически неопределимого бруса
- •3.3 Построение эпюр крутящих моментов
- •Раздел 4. Плоский поперечный изгиб балок. Перерезывающие силы и изгибающие моменты
- •4.1 Перерезывающие силы и изгибающие моменты
- •4.2 Дифференциальные зависимости при изгибе бруса
- •4.3 Построение эпюр изгибающих моментов и перерезывающих сил
- •Глава 3. Напряжения и деформации
- •Раздел 1 Напряженное состояние в точке
- •1.1 Закон парности касательных напряжений
- •1.2. Обобщенный закон Гука
- •1.3 Главные напряжения и главные площадки
- •1.4 Определение компонент напряжений на наклонной площадке. Круговая диаграмма Мора
- •1.5. Определение главных напряжений и угла наклона главных площадок
- •1.6. Определение компонент напряжений на площадке общего положения
- •1.7. Потенциальная энергия деформации
- •Раздел 2. Центральное растяжение и сжатие
- •Историческая справка
- •2.1. Напряжения в поперечных сечениях бруса
- •2.2. Перемещения поперечных сечений бруса
- •2.3. Эпюры нормальных напряжений, деформаций и перемещений при растяжении и сжатии ступенчатого бруса
- •Раздел 3. Сдвиг и срез
- •3.1. Чистый сдвиг
- •3.1.1. Связь между упругими константами материала e, g, и при чистом сдвиге
- •3.2. Касательные напряжения при срезе
- •Раздел 4. Кручение
- •Историческая справка
- •4.1. Кручение бруса круглого и кольцевого поперечных сечений
- •4.1.1. Касательные напряжения в поперечных сечениях бруса
- •4.1.2. Угол поворота поперечного сечения бруса
- •4.1.3. Напряжения в различно ориентированных сечениях и характер разрушения при кручении бруса круглого сечения
- •4.2. Кручение бруса замкнутого тонкостенного сечения
- •4.2.1. Касательные напряжения в поперечных сечениях бруса
- •4.2.2. Угол поворота поперечного сечения бруса
- •4.3. Кручение бруса многосвязного тонкостенного профиля
- •4.4. Кручение бруса прямоугольного сечения
- •4.5. Кручение бруса тонкостенного открытого профиля
- •4.6. Кручение бруса незамкнутого криволинейного профиля переменной толщины
- •4.7. Кручение бруса незамкнутого тонкостенного поперечного сечения, состоящего из нескольких участков различной толщины
- •4.8. Эпюры касательных напряжений, относительных и абсолютных углов закручивания
- •Раздел 5. Плоский прямой изгиб бруса
- •Историческая справка
- •5.1. Нормальные напряжения при чистом изгибе бруса
- •5.2. Нормальные и касательные напряжения при поперечном изгибе бруса. Формула Журавского
- •5.3. Анализ напряженного состояния при поперечном изгибе бруса
- •5.4. Нормальные и касательные напряжения при поперечном изгибе балок тонкостенного профиля
- •5.5. Центр изгиба балки несимметричного тонкостенного профиля
- •5.6. Дифференциальное уравнение упругой линии при поперечном изгибе
- •5.7. Энергетический метод определения перемещений Максвелла‑Мора
- •5.8. Графоаналитический метод определения прогиба балки методом Верещагина
- •5.9. Расслоение эпюр
- •Раздел 6 Косой изгиб прямого бруса
- •6.1. Напряжения относительно главных центральных осей сечения
- •6.2. Напряжения относительно произвольной взаимноперпендикулярной пары центральных осей сечения
- •Раздел 7. Концентрация напряжений
- •7.1. Концентрация напряжений круглого отверстия
- •7.2. Концентрация напряжений эллиптического отверстия
- •7.3. Концентрация напряжений прямоугольного выреза со скругленными углами
- •Раздел 8 Коэффициент интенсивности напряжений
- •Глава 4. Механические свойства конструкционных материалов
- •Раздел 1. Характеристики статической прочности материалов
- •1.1. Диаграммы деформирования. Характеристики материала
- •1.2. Пластические и хрупкие материалы
- •1.3. Закон разгрузки. Явление наклепа
- •1.4. Закон Гука при одноосном растяжении и сжатии
- •1.5. Поперечная деформация. Коэффициент Пуассона
- •Раздел 2 Характеристики сопротивления усталости
- •2.1. Характеристики цикла нагружения
- •2.2. Базовая кривая усталости
- •Раздел 3. Характеристики сопротивления развитию трещины при циклическом нагружении
- •Раздел 4. Характеристики статической трещиностойкости
- •4.1. Характеристики статической трещиностойкости в условиях плоской деформации
- •4.2 Характеристики статической трещиностойкости при плоском напряженном состоянии
- •4.3. Расчетные характеристики статической трещиностойкости
- •Глава 5. Геометрические характеристики плоских сечений
- •1. Статические моменты плоских сечений
- •2. Осевые, центробежный и полярный моменты инерции плоских сечений
- •3. Изменение моментов инерции при параллельном переносе осей
- •4. Изменение моментов инерции при повороте осей координат
- •5. Главные оси и главные моменты инерции. Круг инерции Мора
- •6. Моменты инерции простейших фигур
- •7. Моменты инерции составных сечений
- •Глава 6. Изгиб продольно сжатых стержней
- •Раздел 1. Внецентренное сжатие коротких стержней
- •1.1 Внецентренное сжатие силой, приложенной на одной из главных осей инерции сечения стержня
- •1.2 Внецентренное сжатие силой, которая не находится ни на одной из главных осей инерции сечения стержня
- •Раздел 2. Упругая потеря устойчивости длинных стержней
- •2.1. Упругая потеря устойчивости прямого стержня, нагруженного осевой нагрузкой. Формула Эйлера
- •2.2. Упругая потеря устойчивости стержня, нагруженного осевой нагрузкой с эксцентриситетом
- •2.3. Упругая потеря устойчивости стержня с первоначальной кривизной
- •2.4. Упругая потеря устойчивости стержня, нагруженного осевой и поперечной нагрузками
- •2.4.1. Приближенная формула определения прогиба балки при продольно-поперечном изгибе
- •2.4.2. Дифференциальное уравнение изгибающих моментов при продольно‑поперечном изгибе балки
- •2.5. Энергетический метод определения критической нагрузки
- •2.6. Большие перемещения гибкого стержня
- •Раздел 3. Потеря устойчивости за пределом упругости
- •3.1. Критические напряжения. Пределы применимости формулы Эйлера
- •3.2. Устойчивость стержней за пределом упругости. Модуль Кармана
- •3.3. Формула Ясинского-Тетмайера для определения критических напряжений
- •Глава 7. Статически определимые стержневые системы
- •Историческая справка
- •1. Типы стержневых систем
- •2. Внутренние силовые факторы в сечениях пространственного бруса
- •3. Внутренние силовые факторы в сечениях плоской рамы
- •4. Внутренние силовые факторы в стержнях фермы
- •5. Напряжения в сечениях бруса малой кривизны
- •6. Перемещения сечений пространственного бруса
- •6.1. Потенциальная энергия бруса в общем случае нагружения
- •6.2. Энергетический метод определения перемещений сечений пространственного бруса. Интеграл Мора
- •6.3. Перемещения сечений плоской рамы
- •6.4 Перемещения узлов фермы
- •6.5 Относительные перемещения сечений стержней системы
- •Глава 8. Плоские статически неопределимые стержневые системы
- •1 Кинематический анализ плоских систем
- •2 Метод сил. Канонические уравнения
- •2.1. Внешне статически неопределимые рамы
- •2.2. Внутренне статически неопределимые рамы
- •2.3. Вычисление коэффициентов канонических уравнений
- •2.4. Рациональный выбор основной системы. Использование свойств симметрии при раскрытии статической неопределимости
- •2.5. Последовательность решения статически неопределимых задач
- •3 Перемещения сечений статически неопределимых рам
- •Глава 9. Критерии прочности
- •Раздел 1. Критерии статической прочности
- •1.1 Критерий максимального главного напряжения (Rankine)
- •1.2 Критерий максимальной главной деформации (St. Venant)
- •1.3 Критерий суммарной энергии деформации (Beltramy & Haigh)
- •1.4 Критерий максимальных касательных напряжений (Tresca)
- •1.5 Критерий энергии деформации сдвига (Hencky & VonMises)
- •1.7 Критерий интенсивности напряжений
- •1.8 Критерий Кулона-Мора
- •1.9 Условия текучести при двухосном напряженном состоянии
- •Раздел 2. Критерии сопротивления усталости
- •2.1 Определение приведенных напряжений
- •2.1.1 Приведенные напряжения для элементов с геометрическими концентраторами
- •2.1.2 Приведенное напряжение для продольных стыков крыла
- •2.1.3 Приведенное напряжение для поперечных стыков
- •2.1 Метод «дождевого потока»
- •Раздел 2. Критерии статической трещиностойкости
- •2.1 Энергетический критерий Гриффитса
- •2.2 Критерий разрушения Орована-Ирвина
- •Глава 10 Расчет на прочность
- •Раздел 1 Расчет статической прочности по допускаемым напряжениям
- •1.1 Расчеты на прочность при растяжении и сжатии стержневой системы или ступенчатого бруса
- •1.2 Расчет на прочность при срезе и смятии
- •1.3 Расчет на прочность и жесткость при кручении
- •1.4 Расчет на прочность при изгибе
- •Раздел 2 Расчет статической прочности по предельному состоянию
- •2.1 Расчет на прочность при растяжении сжатии
- •2.2 Расчет на прочность при кручении
- •2.3 Расчет на прочность при изгибе
- •Раздел 3 Расчет на устойчивость
- •3.1 Расчет на устойчивость по аналитическим зависимостям
- •3.2 Расчет на устойчивость по коэффициентам уменьшения основного допускаемого напряжения
- •Литература
5. Напряжения в сечениях бруса малой кривизны
Некоторое влияние на распределение напряжений в сечении бруса и его деформации при изгибе оказывает кривизна оси бруса. Однако, как показали исследования, это влияние становится значительным только при отношении радиуса кривизны оси ρ к высоте h соответствующего поперечного сечения бруса меньше 5. Такой брус называют брусом большой кривизны, или просто кривым брусом. В стержневых системах элементы типа бруса большой кривизны встречаются крайне редко.
В брусе малой кривизны (ρ/h < 5) влияние кривизны оси на напряжения и деформации незначительно, и поэтому расчет таких брусьев на изгиб с достаточной точностью можно производить по формулам для прямого бруса.
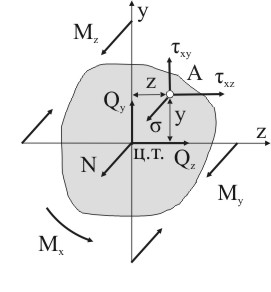
Рисунок 7.23
Если при определении внутренних силовых факторов в качестве осей y и z выбрать главные центральные оси инерции сечения (рис. 7.23), то напряжения в сечении бруса малой кривизны можно вычислить по следующим формулам.
Нормальные напряжения σ:
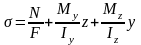 ,
где
,
где
N – нормальная сила;
My, Mz – изгибающие моменты;
Iz, Iy – главные центральные моменты инерции сечения.
Касательные напряжения для сплошного сечения τxy, τxz:
,  ,
,
 ,
где
,
где
Qy, Qz – перерезывающие силы;
Szотс , Syотс – статические моменты отсеченных частей сечения;
b(y), b(z) – ширина сечения;
Wкр – момент сопротивления кручению;
Mx – крутящий момент.
Касательные напряжения для тонкостенного сечения τ:
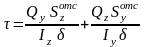 ,
где
,
где
δ – толщина сечения.
6. Перемещения сечений пространственного бруса
Определение перемещений конструкции важно по двум причинам:
- знание характеристик деформирования при нагружении самолета имеет первостепенное значение при изучении влияния упругости конструкции на характеристики самолета;
- вычисление перемещений необходимо при определении внутренних силовых факторов в составных конструкциях с избыточными элементами.
При определении перемещений сечений пространственного бруса необходимо рассматривать общий случай нагружения, когда в поперечных сечениях одновременно возникают нормальные и перерезывающие силы, а также крутящие и изгибающие моменты. В этом случае направление полного перемещения рассматриваемого сечения заранее неизвестно, поэтому вначале определяют проекцию этого перемещения на некоторое выбранное направление, и обозначается δik. Индекс i показывает, перемещение какого сечения и в каком направлении определяется, а индекс k обозначает причину, вызвавшую это перемещение. Если требуется определить полное перемещение δ, то вначале вычисляют проекции перемещения на три взаимно перпендикулярных направления (направления главных центральных осей y и z сечения и касательной к оси x бруса), а затем определяют искомое перемещение:
![]() .
.
Наиболее просто перемещения находятся при помощи энергетических соотношений на основе общего выражения потенциальной энергии нагруженного бруса.
6.1. Потенциальная энергия бруса в общем случае нагружения
Для определения потенциальной энергии выделим из бруса элементарный участок длиной dx (рис. 7.24). Брус может быть не только прямым, но иметь малую начальную кривизну. В каждом из поперечных сечений в общем случае нагружения возникает шесть силовых факторов: три момента и три силы.
По отношению к выделенному элементарному участку рассмотрим эти силовые факторы как внешние и определим работу, которая совершается ими при деформировании элемента. Эта работа переходит в потенциальную энергию, накопленную в элементарном участке бруса.
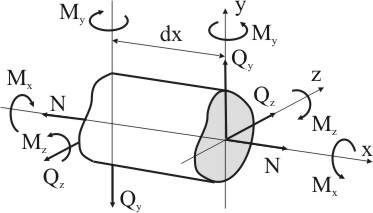
Рисунок 7.24
Потенциальную энергию определим при следующих допущениях:
а) брус подвергается упругому деформированию;
б) точка приведения сил вследствие деформации элемента получает некоторые малые перемещения, на которых совершается искомая работа;
в) каждому из шести силовых факторов соответствуют такие перемещения, на которых ни один из остальных пяти работы не совершает; потенциальная энергия элемента может рассматриваться как сумма независимых работ каждого из шести силовых факторов, т. е., иначе говоря, как сумма энергии кручения, изгиба, растяжения и сдвига:
dU = dU(Mx) + dU(My) + dU(Mz) + dU(N) + dU(Qz) + dU(Qy)
г) оси z и у являются главными центральными осями поперечного сечения бруса.
В общем случае для сложного напряженного состояния упругая потенциальная энергия в единице объема определяется выражением:
U0 = (1/(2E)) [σx2 + σy2+ σz2 - 2μ (σx σy + σx σz + σy σz )] + (1/(2G)) (τyz2 + τxy2 + τxz2)
Для того чтобы получить потенциальную энергию во всем объеме деформированного тела, выражение U0 следует умножить на элементарный объем и проинтегрировать по объему тела:
В случае одноосного растяжения в сечении возникает только один силовой фактор‑нормальная сила N, которая обусловлена действием нормальных напряжений σx. Остальные компоненты напряжений σy = σz = τyz = τxy = τxz = 0. Потенциальная энергия dU(N) в элементарном объеме F dx может быть подсчитана:
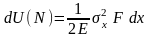
Учитывая, что
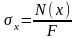 ,
то после подстановки получим:
,
то после подстановки получим:
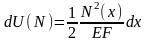
Интегрируя по длине бруса l, находим суммарную потенциальную энергию:
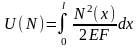 (1)
(1)
При кручении в сечении бруса возникает крутящий момент, который обусловлен действием касательных напряжений τ. При этом остальные компоненты напряжений σx = σy = σz = τyz = 0. Потенциальная энергия dU(Mx) в элементарном объеме F dx может быть подсчитана:
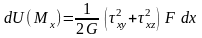
Учитывая, что
 и
и
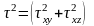 ,
то после подстановки получим:
,
то после подстановки получим:

Интегрируя по длине бруса l, находим суммарную потенциальную энергию:
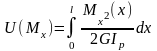 (2)
(2)
В случае поперечного изгиба в поперечном сечении бруса возникают изгибающие моменты My, Mz, которые обусловлены действием нормальных напряжений σx, и перерезывающие силы Qy, Qz, которые обусловлены действием касательных напряжений τxy, τxz. Учитывая, что σy = σz = τyz = 0, потенциальная энергия dU(My) в элементарном объеме F dx может быть подсчитана:
dU
= dU(My)
+ dU(Mz)
+ dU(Qz)
+ dU(Qy)
=
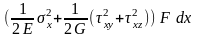 (3)
(3)
Нормальные напряжения от действия изгибающих моментов My, Mz соответственно:
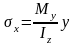 ,
, 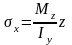 (4)
(4)
Касательные напряжения от действия перерезывающих сил Qy, Qz определим по формуле Журавского:
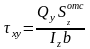 ,
,
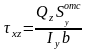 (5)
(5)
Подставим соотношения (4) и (5) в выражение (3), получим выражение потенциальной энергии в элементарном объеме при поперечном изгибе:
 ,
,
здесь ky, kz – коэффициенты, учитывающие неравномерность распределения касательных напряжений по сечению при изгибе.
Интегрируя по длине бруса l, находим суммарную потенциальную энергию:
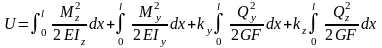 (6)
(6)
Просуммировав соотношения (1), (2) и (6), получим выражение потенциальной энергии пространственного бруса:

