6. Моменты инерции простейших фигур

Распространенными формами поперечных сечений бруса являются простейшие фигуры (прямоугольник, треугольник, круг, кольцо и т.д.) или их комбинации.

Для удобства проведения расчетов выведем формулы, по которым можно определить их моменты инерции.

Прямоугольник и параллелограмм.

Для прямоугольника и параллелограмма момент инерции относительно главной центральной оси z_c:

Для определения dF выделим элементарную полоску шириной dy на расстоянии y от оси z_с (рис. 5.7), тогда:

dF = b  dy

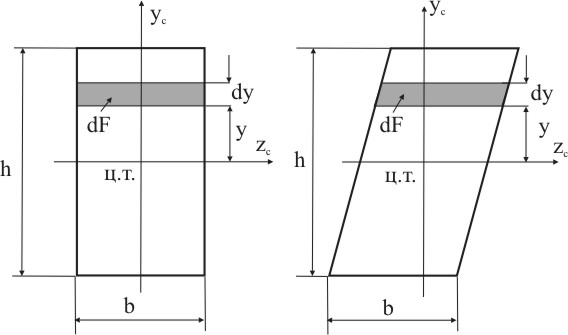
Рисунок 5.7

Подставим это выражение dF под знак интеграла I_zc:

Аналогично можно получить формулу главного центрального момента инерции I_yc для прямоугольника относительно оси y_c:

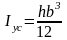
Для прямоугольника центробежный момент инерции относительно прямоугольной системы координат, оси которой параллельны главным осям сечения (рис. 5.8):

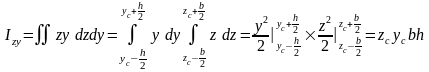
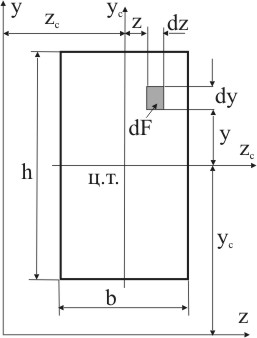
Рисунок 5.8

Треугольник.

Вычислим момент инерции сечения треугольной формы относительно оси z проходящей через основание:

Выделим элементарную полоску шириной dy на расстоянии y (рис. 5.9), тогда:

dF = b(y)  dy =

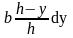
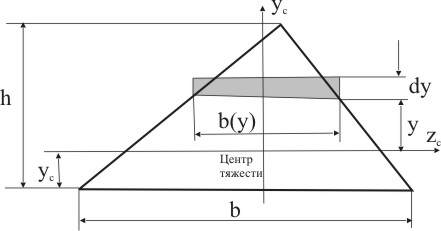
Рисунок 5.9

Подставим под знак интеграла:

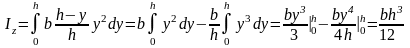
Определим момент инерции относительно центральной оси z_c. Для этого вначале определим координату центра тяжести y_c:

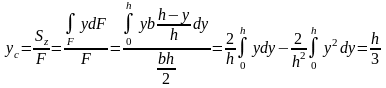
Используя формулы изменения моментов инерции при параллельном переносе осей, запишем:

I_z = I_zc + y_c² F, откуда:

I_zc = I_z – y_c² F =

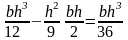
Круг и полукруг.

Осевые моменты инерции круга определим с помощью соотношения:

I_p = I_zc + I_yc

В силу симметрии круга:

I_zc = I_yc = I_p / 2

Для вычисления полярного момента инерции I_p выделим элементарное кольцо шириной dρ на расстоянии ρ от центра круга (рис. 5.10).

Площадь элементарного кольца:

dF = 2πρ dρ

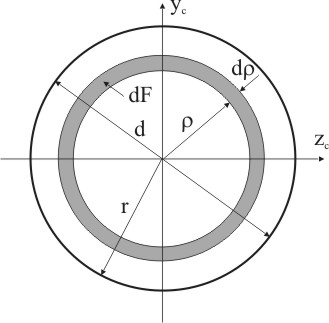
Рисунок 5.10

Полярный момент инерции:

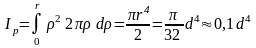
Следовательно, осевые моменты инерции круга:

I_zc = I_yc = I_p / 2 0,05d⁴

Так как ось z_c делит круг пополам, то момент инерции полукруга I_z относительно оси z проходящей через основание:

I_z = I_zc /2 0,025d⁴

Момент инерции четверти круга I_z относительно оси z проходящей через основание:

I_z 0,0125d⁴

Вычислим центробежный момент инерции четверти круга: I_zy:

(1)

Для вычисления центробежного момента инерции I_zy выделим элементарный участок dF двумя кольцевыми сечениями на расстоянии dρ друг от друга и на расстоянии ρ от центра четверти круга и двумя радиусными сечениями с раствором dθ на расстоянии θ от оси z (рис. 5.11).

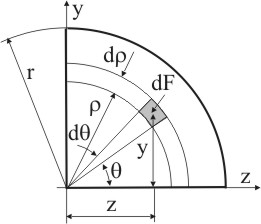
Рисунок 5.11

Площадь элементарного кольца:

dF = ρ dθ dρ

Координаты центра элементарного участка z и y:

z = ρ cosθ

y = ρ sinθ

Подставим выражения dF, z и y в (1) получим центробежный момент инерции четверти круга:

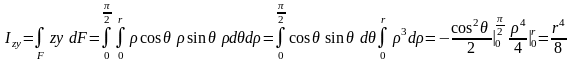
Тонкостенное кольцо и полукольцо.

Выделим элементарный сектор двумя радиусами, отстоящими друг от друга на расстоянии d (рис. 5.12).

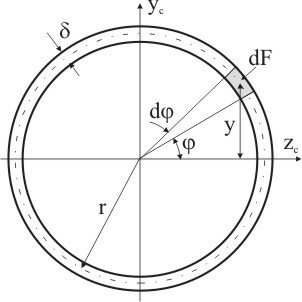
Рисунок 5.12

Площадь элементарного сектора:

dF = r d δ

Момент инерции кольца относительно оси z_c:

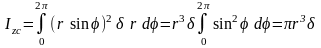
Момент инерции тонкостенного полукольца относительно оси z проходящей через основание:

I_z = I_zc / 2 = (πr³ δ)/2