Раздел 1 Напряженное состояние в точке

Для того чтобы определить напряженное состояние вокруг какой либо точки конструкции, вырежем элементарный параллелепипед с бесконечно малыми сторонами dx, dy, dz внутри которого находится исследуемая точка, и на гранях этого параллелепипеда определим нормальные и касательные напряжения (рис. 3.4а). Если устремлять стороны параллелепипеда к нулю, то есть стягивать их в точку, то в пределе получим исследуемую точку, а напряжения, действующие на гранях параллелепипеда, будут напряжениями в этой точке.

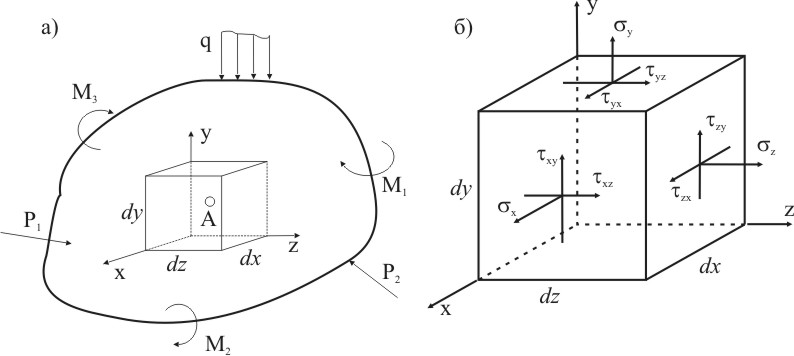
Рисунок 3.4

В общем случае на гранях элементарного параллелепипеде требуется определить шесть компонентов перемещений (3 компонента нормальных σ и 3 компонента касательных напряжений τ) (рис. 3.4б). На рисунке для наглядности изображены компоненты напряжений только на видимых гранях параллелепипеда. На невидимых гранях параллелепипеда возникают соответственно такие же напряжения, но противоположно направленные. Индекс нормальных напряжений совпадает с наименованием оси, параллельно которой направлен вектор нормальных напряжений. Касательные напряжения имеют два индекса, первый совпадает с наименованием оси, к которой перпендикулярна рассматриваемая грань, а второй совпадает с наименованием оси, параллельно которой направлен вектор напряжения. Предполагается, что перепады нормальных и касательных напряжений на длинах dx, dy, dz отсутствуют.

1.1 Закон парности касательных напряжений

Так как система сил, действующая на грани параллелепипеда, выделенного из объема (рис. 3.4б), должна находиться в равновесии, то для нее должны удовлетворять уравнениям равновесия:

 x =0  mom_x=0

 y =0  mom_y=0

 z =0  mom_z=0

Поскольку на противоположных гранях возникают противоположные по направлению силы, то три условия равновесия удовлетворяются тождественно, т.е. суммы проекций всех сил на оси x, y, z равны нулю, независимо от величины возникающих напряжений. Остается проверить, обращаются ли в нуль суммы моментов относительно осей x, y, z.

Запишем уравнения равновесия моментов относительно оси x.

mom_x = σ_ydxdz(dx/2)- σ_ydxdz(dx/2)+σ_zdxdy dy/2)-σ_zdxdydy/2)+

+τ_xydydz(dz/2)- τ_xydydz(dz/2) +τ_xzdydz(dz/2)- τ_xzdydz(dz/2) +τ_yzdydzdx-τ_zydy dx dz =0, откуда

τ_yz = τ_zy

Из уравнений равновесия относительно осей y и z аналогично можно получить:

τ_xz = τ_zx

τ_yx = τ_xy

Полученные равенства называют законом парности касательных напряжений, который можно сформулировать следующим образом.

Касательные напряжения на двух взаимно ортогональных площадках равны по величине и направлены либо к линии пересечения площадок, либо от нее.

1.2. Обобщенный закон Гука

Между компонентами напряженного состояния, с одной стороны и деформированного ‑ с другой существует определенная зависимость. В пределах малых деформаций эта зависимость является линейной и носит название обобщенного закона Гука. Запишем закон Гука для объемного напряженного состояния для изотропного тела (без учета температур). В этом случае коэффициенты пропорциональности между компонентами напряжений и деформаций не зависят от ориентации осей в точке. Кроме того деформации от каждой из компонент напряжений не влияют друг на друга. Поэтому чтобы составить аналитическое выражение обобщенного закона Гука, воспользуемся принципом независимости действия сил и рассмотрим раздельно силы, возникающие на гранях элементарного параллелепипеда. Для этого рассмотрим единичный параллелепипед, на гранях которого действуют только нормальные напряжения (рис. 3.5).

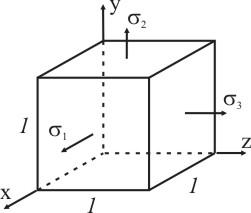
Рисунок 3.5

Экспериментально установлено, что при упругих деформациях для одноосного напряженного состояния (₁≠0, ₂=0, ₃=0) существует линейная зависимость между линейной деформацией и нормальным напряжением (закон Гука):

, где

E – модуль упругости, или модуль Юнга;

₁ – нормальное напряжение;

ε₁= линейная относительная деформация.

Одновременно с линейной деформацией ε₁ в перпендикулярных направлениях возникают деформации ε₂, ε₃:

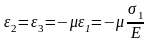, где

μ – коэффициент Пуассона.

На основании принципа независимости действия сил, можно записать, что деформация в направлении σ₁ при суммарном действии напряжений σ₁, σ₂ и σ₃:

, где

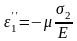
Следовательно:

(1)

Таким образом, при всестороннем растяжении деформации вызванные напряжениями σ₂ и σ₃ за счет эффекта Пуассона уменьшают деформацию вызванную σ₁. Аналогично:

(2)

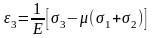(3)

Экспериментально также установлено, что при чистом сдвиге существует линейная зависимость между угловой деформацией и касательным напряжением:

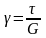, где

γ - угол сдвига,

τ – касательное напряжение,

G - модуль сдвига, или модуль упругости второго рода.

Предполагая, что для объемного напряженного состояния при сдвиге компоненты напряжений не влияют друг на друга, тогда по аналогии с простым случаем чистого сдвига можно записать:

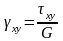
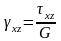(4)

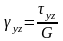, где

γ_xy, γ_xz, γ_yz - углы сдвига.

Зависимости деформаций от напряжений (1-4) носят название обобщенного закона Гука, или закона Гука для объемного напряженного состояния.

Если сложить левые и правые части зависимостей (1-3) получим значение объемной деформации е=ε₁ +ε₂ +ε₃:

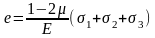
В случае равномерного всестороннего растяжения, т.е. при σ₁=σ₂=σ₃=p:

Из анализа полученной зависимости видно, что при p>0 только при μ≤0,5 объемная деформация e>0. Следовательно, значение μ для изотропного материала не может превышать 0,5.