1.5. Определение главных напряжений и угла наклона главных площадок

Задача заключается в том, чтобы по известным значениям нормальных и касательных напряжений на гранях элементарного параллелепипеда определить значения главных напряжений и угол наклона главной площадки. Рассмотрим случай двухосного напряженного состояния (рис. 3.10).

Рисунок 3.10

Для заданного напряженного состояния строим круг Мора (рис. 3.11):

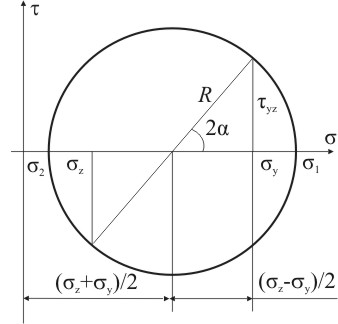
Рисунок 3.11

Радиус круга Мора можно записать:

.

Следовательно, главные напряжения:

.

Угол наклона главной площадки определяется соотношением:

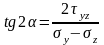
1.6. Определение компонент напряжений на площадке общего положения

Если заданы шесть компонентов напряженного состояния, а именно σ_x, σ_y, σ_z, и τ_xy, τ_xz, τ_yz в трех взаимно перпендикулярных площадках, то можно определить напряжения вообще в любой площадке, проходящей через данную точку. Из напряженного объема конструкции (рис. 3.4а) еще раз выделим в окрестности точки A элементарный объем, но уже не в виде параллелепипеда, как было сделано ранее, а в виде четырехгранника (рис. 3.12а).

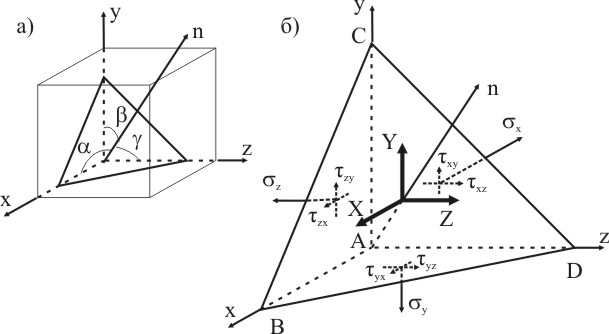
Рисунок 3.12

Три грани выделенного элемента совпадают с координатными плоскостями системы x, y, z. Четвертая грань образована секущей плоскостью общего положения. Ее ориентацию в пространстве будем определять направляющими косинусами нормали n, т. е. величинами:

l = cos α, m = cos β, k = cos γ.

Элементарный четырехгранник обладает теми же свойствами, что и рассмотренный выше параллелепипед. При уменьшении размеров он стягивается в точку A, и в пределе все его грани проходят через эту точку. Поэтому напряжения на гранях элемента рассматривают как напряжения в исследуемой точке, но в площадках различным образом ориентированных. На рисунке 3.12б пунктиром показаны составляющие напряжений на невидимых гранях. Вектор полного напряжения на площадке общего положения BCD спроектируем на оси x, y, и z. Обозначим эти проекции через X, Y и Z соответственно. Если эти три величины найдены, то по ним, очевидно, могут быть найдены нормальная и касательные составляющие на площадке общего положения.

Площадь треугольника BCD обозначим через F, треугольника ACD через F_x, ABD через F_y и, наконец, треугольника ABC через F_z. Очевидно,

F_x = F l, F_y = F m, F_z = F k (1)

где l, m и k — направляющие косинусы нормали n.

Проектируя все силы, действующие на элемент, последовательно на оси х, у и z, получим:

Σx = X F- σ_x F_x + τ_yx F_y + τ_zx F_z = 0

Σy = Y F– σ_y F_y + τ_xy F_x+ τ_zy F_z = 0

Σx = Z F– σ_z F_z + τ_xz F_x + τ_yz F_y = 0,

откуда в соответствии с соотношениями (1):

X = σ_x l - τ_yx m - τ_zx k

Y = σ_y m - τ_xy l - τ_zy k (2)

Z = σ_z k- τ_xz l - τ_yz m

Таким образом, действительно для любой площадки, определяемой направляющими косинусами l, m и n, проекции X, Y и Z выражаются через шесть исходных компонентов σ_x, σ_y, σ_z, и τ_xy, τ_xz, τ_yz. Иными словами, напряженное состояние в точке определяется шестью компонентами. При помощи формул (2) легко определяется вектор полного напряжения p на любой площадке, проходящей через рассматриваемую точку:

p² = X² + Y² + Z² (3)

Таким образом, напряженное состояние в точке представляет собой понятие, более сложное, чем те, которыми мы оперировали до сих пор. Выразим через X, Y, Z нормальное напряжение σ_n в наклонной площадке:

σ_n = X l + Y m + Z k

После подстановки выражений (2) и преобразований, получим:

σ_n = σ_x l² + σ_y m² σ_k k² - 2τ_xy l m - 2τ_xz k l - 2τ_yz m k

Касательное напряжение τ_n на наклонной площадке:

τ_n² = p² - σ_n², где (4)

Положим, что оси x, y, z главные и σ_x = σ₁, σ_y = σ₂, σ_z = σ₃, τ_xy = τ_xz = τ_yz = 0, тогда выражения (2) примут вид:

X = σ₁ l, Y = σ₂ m, Z = σ₃ k.

Полное напряжение согласно выражению (3):

p² = X² + Y² + Z² = σ₁² l² + σ₂² m² + σ₃² k²

Нормальное напряжение на наклонной площадке:

σ_n = X l + Y m + Z n = σ₁ l² + σ₂ m² +σ₃ k²

Подставляя выражения p² и σ_n в соотношение (4), получим выражение касательного напряжения τ_n на наклонной площадке:

τ_n² = (σ₁ - σ₂)² l²m² + (σ₁ - σ₃)² l²k²+(σ₂ - σ₃)² k²m²

Если нормаль n совпадает с одной из главных осей, то один из направляющих косинусов принимает значение равное единице, а два других равны нулю, и тогда τ_n = 0.

Определим напряжения на октоэдрической площадке σ_oct, τ_oct, т.е. площадке равнонаклоненной к главным площадкам. Для таких площадок l² = m² = k² = 1/3, и тогда получим:

σ_oct = 1/3 (σ₁ + σ₂ + σ₃)

τ_oct =

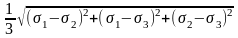
Пример 3.1

Для заданного напряженного состояния, которое показано на рисунке 3.13, определить главные напряжения и угол наклона главных площадок. Построить круг Мора.

Решение.

1. Так как на площадке yz отсутствуют касательные напряжения, она является главной, а напряжение σ_x =50 - главное напряжение.

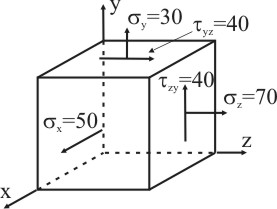
Рисунок 3.13

2. Вычислим величины главных напряжений на двух других площадках:

Выстроим главные напряжения по возрастающей, получим:

σ₁ = 94,7; σ₂ = 50; σ₃ = 5,3.

3. Определим угол поворота главных площадок.

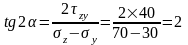, откуда

α=31,7

4. Изобразим элемент повернутым так, чтобы все его грани стали главными (рис. 3.14б).

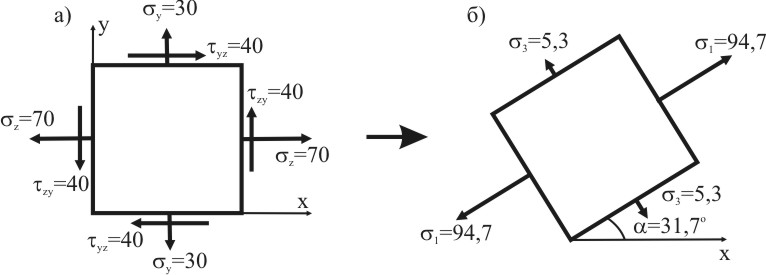
Рисунок 3.14

5. Построим диаграмму напряжений Мора (рис. 3.15).

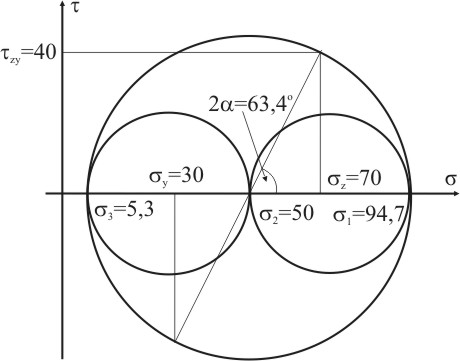
Рисунок 3.15