1.3 Главные напряжения и главные площадки

Главными нормальными напряжениями называются такие напряжения, которые действуют на площадках элементарного параллелепипеда, на которых отсутствуют касательные напряжения. Площадка, на которой отсутствуют касательные напряжения, является главной. Главные нормальные напряжения дают возможность разделить напряженное состояние на три вида:

- одноосное (рис. 3.6а);

- двухосное (рис. 3.6б);

- трехосное (рис. 3.6в).

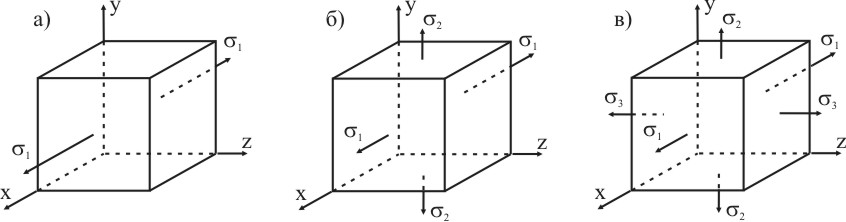
Рисунок 3.6

В дальнейшем принимаем, что:

σ₁ ≥σ₂ ≥σ₃.

Главные напряжения обладают следующими свойствами.

1-ое свойство (свойство инвариантности).

При любой ориентации осей координат в пространстве тройка главных напряжений остается неизменной, т.е. главные напряжения инвариантны относительно осей координат.

2-ое свойство (свойство стационарности).

Одно из главных напряжений является максимальным напряжением из всех нормальных напряжений в точке (σ₁=σ_max), а другое является минимальным (σ₃=σ_min).

1.4 Определение компонент напряжений на наклонной площадке. Круговая диаграмма Мора

По известным значениям главных напряжений σ₁, σ₂, σ₃ определим напряжения действующие на накладной площадке. Пусть на гранях элементарного параллелепипеда задана тройка главных напряжений σ₁  σ₂  σ₃. Необходимо определить напряженное состояние на любой площадке параллельной одному из векторов главных напряжений, в частности, вектору σ₁ (рис. 3.7а). Эта площадка может иметь со смежной гранью произвольный угол α. Выделим отсеченную часть - трехгранную призму, на которую действуют заданные главные напряжения σ₁, σ₂, σ₃, и на наклонной площадке действуют нормальные напряжения σ_α и касательные напряжения τ_α, которые необходимо определить (рис. 3.7б). На рисунке n- внешняя нормаль, приведенная к площадке S, а t -касательная, лежащая в плоскости S и перпендикулярная n.

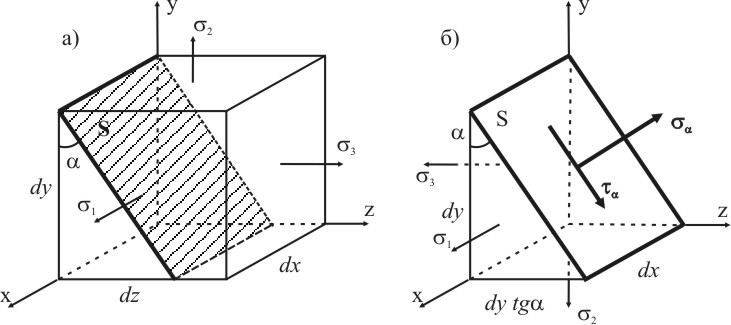
Рисунок 3.7

Проецируя усилия действующие на призму на оси n и t получим:

n = σ_α dx (dy/cosα)- σ₂ sinα dx dy tgα - σ₃ cosα dx dy =0,

t = τ_α dx (dy/cosα)+σ₂ cosα dx dy tgα - σ₃ sinα dx dy =0,

откуда:

σ_α= σ₂ sin²α+ σ₃ cos² α

τ_α = (σ₂- σ₃) sinα cosα

Преобразуем полученные соотношения к виду:

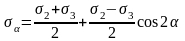
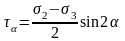
Этим выражением можно дать геометрическое толкование. Перемещая в левую часть, возводя левые и правые части выражений в квадрат и складывая, получим:

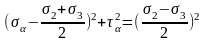
Это уравнение окружности в системе координат «σ-τ» (рис. 3.8).

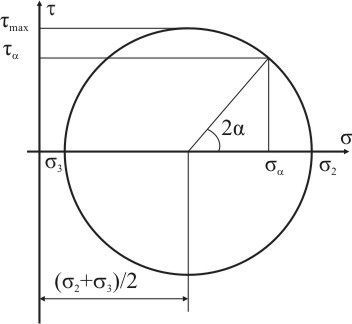
Рисунок 3.8

Центр окружности находится на оси абсцисс на расстоянии от начала координат с радиусом . Окружность называют круговой диаграммой Мора. Полученное уравнение окружности может быть истолковано, как параметрическое уравнение окружности, где роль параметра играет угол α наклона плоскости S. Каждой секущей площадке соответствует определенная точка на круге Мора. Показанная на рисунке 3.8 окружность построена для семейства площадок, параллельных вектору σ₁.

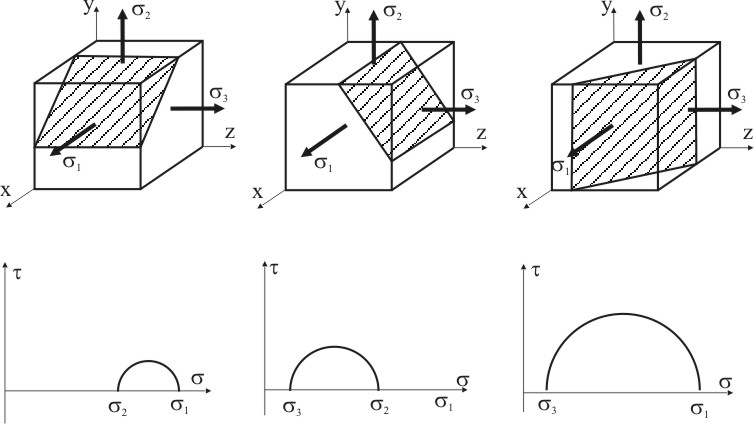
Рисунок 3.9

Аналогичным способом можно построить круги Мора для семейств площадок, параллельных векторам σ₂, σ₃. В этих случаях круги строятся соответственно на отрезках «σ₂‑σ₃» и «σ₁‑σ₂», как на диаметрах. Таким образом, может быть построено три круга Мора (рис. 3.9). Поскольку знак τ не оговаривается, ограничиваются обычно построением только верхней части круга.