Раздел 3. Потеря устойчивости за пределом упругости
3.1. Критические напряжения. Пределы применимости формулы Эйлера
Для вывода формулы Эйлера использовалось дифференциальное уравнение упругой линии стержня, которое справедливо только в случае, когда материал стержня подчиняется закону Гука. Отсюда следует, что формулой Эйлера можно пользоваться только тогда, когда критические сжимающие напряжения не превышают предела пропорциональности. Чтобы судить о пределах применимости формулы Эйлера, разделим обе части формулы на площадь поперечного сечения F. Слева мы получим критическое сжимающее напряжение:
кр
=
.
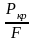Введем величину
r =
,
имеющую размерность длины, которую
называют радиусом инерции сечения.
Также введем безразмерную величину λ,
называемую гибкостью стержня:
.
Формула Эйлера перепишется следующим образом:
кр=
.
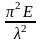Для длинных, тонких стержней велико, следовательно, критическое напряжение мало. Предельным случаем для применения формулы будет тот, когда кр равно пределу пропорциональности пц, т.е.:
=
пц.
Предельное значение гибкости, при которой напряжения становятся равными пределу пропорциональности:
.
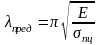Предельное значение гибкости для некоторых материалов приведены в таблице 6.2.
Таблица 6.2
№ |
Материал |
пред |
1 |
Сталь Ст.2 |
105 |
2 |
Сталь Ст.3 |
100 |
3 |
Стали Ст.4, Ст.20 |
96 |
4 |
Сталь Ст.45 |
85 |
5 |
Дуралюмин Д-16 |
53 |
При гибкости стержня, меньшей пред, формула Эйлера неприменима, и задача об устойчивости стержня требует особого рассмотрения.
3.2. Устойчивость стержней за пределом упругости. Модуль Кармана
Рассмотрим устойчивость стержня произвольного сечения за пределом упругости (рис. 6.14а).
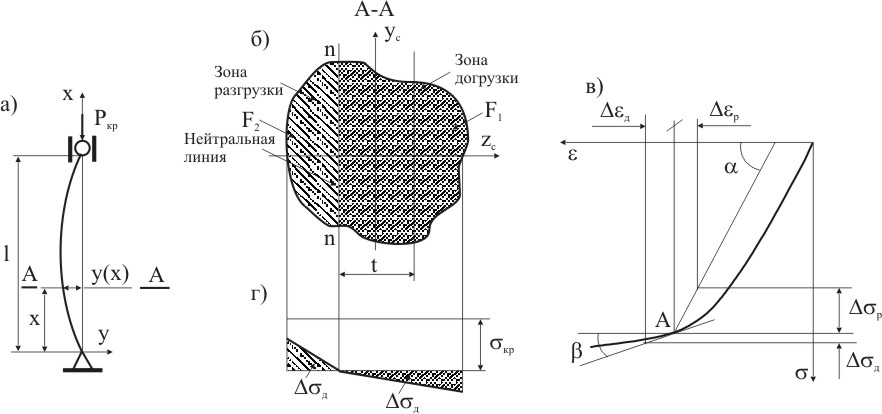
Рисунок 6.14
При достижении Pкр устанавливается новая форма равновесия стержня с искривленной осью. От действия осевой силы в стержне возникают сжимающие нормальные напряжения кр, а от изгиба нормальные напряжения, которые вызывают нагрузку одной части сечения и разгрузку другой.
Для решения задачи принимают следующие допущения:
1) прогибы
малы, поэтому применимо дифференциальное
уравнение упругой линии для симметричного
изгиба
;
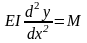2) выполняется гипотеза плоских сечений, поэтому сохраняется такой же, как и для изгиба, зависимость между деформацией и кривизной упругой линии Δε = (1/ρ) t;
3) диаграмма деформирования соответствует диаграмме деформирования при растяжении-сжатии материала стержня;
4) форма упругой линии при потере устойчивости такая же, как и форма упругой линии при симметричном изгибе.
С вогнутой стороны сжимающие напряжения увеличатся (рис. 6.14г), и связь между изменением напряжения и деформации будет изображаться кривой нагрузки, т.е. участком кривой деформирования от точки A вниз (рис. 11.13в). При малом изменении напряжений эту кривую можно заменить касательной к кривой деформирования в точке A. Тогда, величину догрузки Δσд можно оценить:
Δσд = Eк Δεд, где
Eк = tgβ - касательный модуль упругости.
В точках, расположенных с выпуклой стороны изогнутого стержня, происходит разгрузка (рис. 6.14г). Величину разгрузки Δσр оценим по участку разгрузки на диаграмме деформирования (рис. 6.14в):
Δσр = E Δεр, где
E = tgα - модуль упругости.
Так как при потере устойчивости справедлива гипотеза плоских сечений, поэтому, как и при изгибе:
Δε = (1/ρ) t, где
t - расстояние точки сечения от нейтральной оси n-n, положение которой, заранее неизвестно;
ρ - кривизна деформированной оси стержня.
Соответственно, для зон догрузки и разгрузки, получим:
Δσд = Eк (t/ ρ), Δσр = E (t/ ρ). (1)
При малом искривлении стержня нормальная сила в поперечном сечении остается неизменной, поэтому:
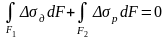
Подставим выражения (1) и после преобразований получим:
Eк S1 = E S2, (2)
где S1 и S2 – статические моменты зоны догрузки и зоны разгрузки относительно нейтральной оси. При заданном напряжении кр, а следовательно Eк, из полученного уравнения (2) путем последовательных проб определяется положение нейтральной оси.
Вычислим теперь момент относительно нейтральной оси «n‑n», создаваемый дополнительными напряжениями Δσд, Δσр:
, (3)
где I1, I2 - моменты инерции площадей F1 и F2 относительно оси «n‑n».
Зависимость (3) устанавливает связь между дополнительным изгибающим моментом и кривизной. В упругой области эта зависимость можно представить в виде:
где I – момент инерции всего сечения относительно главной центральной оси;
Величина Eпр называется приведенным модулем или модулем Кармана.
Как видно приведенный модуль зависит не только от материала, но и от формы поперечного сечения. Теперь можно рассматривать потерю устойчивости сжатого стержня совершенно так же, как потерю устойчивости в упругой области. В дифференциальном уравнении изгиба нужно заменить модуль упругости E модулем Кармана Eпр.
В результате критическая сила:
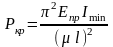(4)
критические напряжения определяются трансцендентным уравнением:
кр=
.
Так как величина Eпр зависит от касательного модуля Eк, а тот в свою очередь от кр, то величина критического напряжения зависит от вида диаграммы деформирования и формы поперечного сечения.
В случае, если материал стержня деформируется упруго, нейтральная линия совпадает с главной центральной осью сечения, I1 + I2 = I и Eпр = E. Тогда формула (4) совпадает с формулой Эйлера. Для нессиметричного сечения не безразлично, с какой стороны от нейтральной линии расположены зона догрузки и зона разгрузки. Это означает, что изгиб стойки в одну и другую стороны не равновероятен. Для того, чтобы решить, в какую сторону происходит изгиб, надо после подсчета Eпр поменять местами зоны догрузки и разгрузки и провести расчет заново. Из двух значений Eпр необходимо выбрать наименьшее.
Пример 11.5
Определить критическую нагрузку при сжатии стержня прямоугольного сечения размерами a×b. Стержень длиной l шарнирно закреплен. Для материала стержня задана идеализированная диаграмма деформирования (рис.6.15):
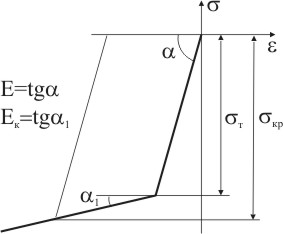
Рисунок 6.15
Решение.
1. Определим положение нейтральной оси из соотношения: Eк S1 = E S2.
Рисунок 6.16
Статические моменты относительно нейтральной оси «n‑n» (рис. 6.16).
S1 = h ξa (a/2)ξ
S2 = h a(1-ξ) (a/2)(1-ξ),
Подставим эти выражения в соотношение, получим:
(E-Eк) ξ2 -2 E ξ + E =0.
Решая полученное уравнение, получим:
.
2. Моменты инерции частей сечения относительно нейтральной оси «n‑n».
,
.
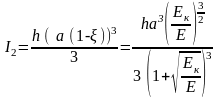Момент инерции полного сечения относительно главной центральной оси yc:
.
3. Определим приведенный модуль Кармана.
4. Определим величину критической силы. Так как стержень шарнирно закреплен μ=1.
