7.2. Нелінійне програмування в операційному менеджменті

Операційний менеджер постійно стикається із ситуаціями коли проблему взаємовідносин між змінними в економічних системах коректно описати лінійними функціями неможливо. Спроба врахувати приривчасто діючи фактори на процеси прийняття рішень спонукає звернутись до формулювання більш складних ніж лінійні оптимізаційних задач. Дослідження методів рішення цих задач отримали назву нелінійного програмування.

Загальна задача нелінійного програмування (ЗЗНП) визначається як задача пошуку максимуму (чи мінімуму) цільової функції f(х₁, х₂,...,х_n) на множині D, що визначається системою обмежень.

За звичай до нелінійного програмування віднесені задачі такого типу: максимізувати с(х₁, х₂, ...., х_n), (7.1) при умові а_i(х₁, х₂, ...., х_n) ≤ 0, 1 = 1,2,…, m, (7.2), де: як с(х₁,...,х_n), так і а₁(х₁,...., х_n) являють собою дійсні, нелінійні, але регулярні функції n дійсних змінних. За суттю (7.1) і (7.2) можна розглядати як кононічну форму задачі нелінійного програмування, оскільки відомі методи дозволяють інтерпретувати оптимізацію як ”максимізацію”, а обмеження - як нерівності. Обмеження позитивності змінної х_j також можуть бути включені у (7.2) у вигляді -х_j ≤ 0.

Зауважимо, що до (7.2) завжди можна включити нелінійні обмеження, завдяки яким у припустимі рішення моделі будуть входити лише цілочисельні значення тих чи інших змінних. Наприклад, хай х_j повинен приймати значення лише 0 або 1. Здійснення цієї умови цілочисельності можна забезпечити, наклавши обмеження - х_j≤ 0, х_j - 1≤ 0 і х_j(1-x_j) ≤ 0. Додамо, що значення нелінійного програмування і його використання в менеджменті постійно зростає, що обумовлене зростаючими знаннями керівників і спеціалістів щодо управління операціями у частині використання математичних моделей прийняття рішень, можливістю комп’ютерного рішення нелінійних задач великої розмірності.

У більшості випадків нелінійності, які необхідно відображувати у моделях, відносяться до однієї із двох категорій:

-співвідношення, що емпірично спостерігаються (такі як непропорційні зміни витрат, виходу продукції, показників якості);

- структурно отримані співвідношення до яких відносять постульовані фізичні явища, а також виведені математично або встановлені керівництвом правила поведінки. Вочевидь, відокремлення цих двох категорій неможливо, оскільки при наявності достатньої кількості даних можна ввести співвідношення, що покладені до основи явища, яке емпірично спостерігається.

Прикладом першої категорії слугуватиме випадок, коли на підприємстві у продовж декілька років приріст виробництва продукції відстає від росту витрат праці в той час, як темпи зростання кількості відходів його випереджає. Прикладом моделі другої категорії є фірма, яка повинна сплачувати рахунок за електрику у випадку коли розрахунки відбуваються за нелінійною формулою, що враховує як середньо добові витрати так і „пікову” потребу. У даному випадку фірма отримує повідомлення про нелінійний характер витрат із договору щодо ставки платні, який було обумовлено із постачальником електрики.

Варіанти встоювання „нелінійності” у моделі програмування зустрічаються і в інших випадках :

• виготовлення бензинових сумішей;

• управління виробничим процесом;

• доходність від реалізації продукції.

Щоб проілюструвати останнє приймемо, що х(р) – об’єм реалізації, який залежить від ціни р, коли доходність від реалізації дорівнює рх(р) . Хай на інтервалі, що нас цікавить, змінення р функція об’єма реалізації від ціни лінійна, тобто має вигляд х(р) = ар + b. В такому разі складові у цільової функції, що відносяться до виручки від реалізації є квадратичними відносно управляючої змінної р і має вигляд (ар² + bp).

Властивості ЗНП, що ускладнюють процес їх рішення відносно до задач ЛП:

1. Множина припустимих планів D може мати дуже складну структуру;

2. Глобальний максимум (мінімум) може досягатися як в середині множини D, так і на його межах;

3. Цільова функція f може бути такою, що не диференціюється, а таке значно утруднює застосування класичних методів математичного аналізу.

Одним із найбільш поширених підходів до рішення задач пошуку екстремуму функції при наявності зв’язуючих обмежень на її змінні (задачі умовної оптимізації) є метод Лагранжа. Ідея методу полягає у зведенні задачі пошуку умовного екстремуму цільової функції f(x₁, x_{2, ,..,} x_n ) на множині припустимих значень D, що описуються системою рівнянь до задачі безумовної оптимізації функції Ф(x,u) = f(x₁,x₂,…,x_n) + u₁g₁(x₁,x₂,…,x_n)+…+ u_mg_m(x₁,x₂,…,x_n), де: - вектор додаткових змінних, які звуться множниками Лагранжа. Функція Ф(x,u), де , відповідно є функцією Лагранжа.

Спираючись на вище визначене, метод Лагранжа містить наступні етапи:

1.Складання функції Лагранжа Ф(х, и)

2.Знаходження часних похідних і

3.Вирішення системи рівнянь

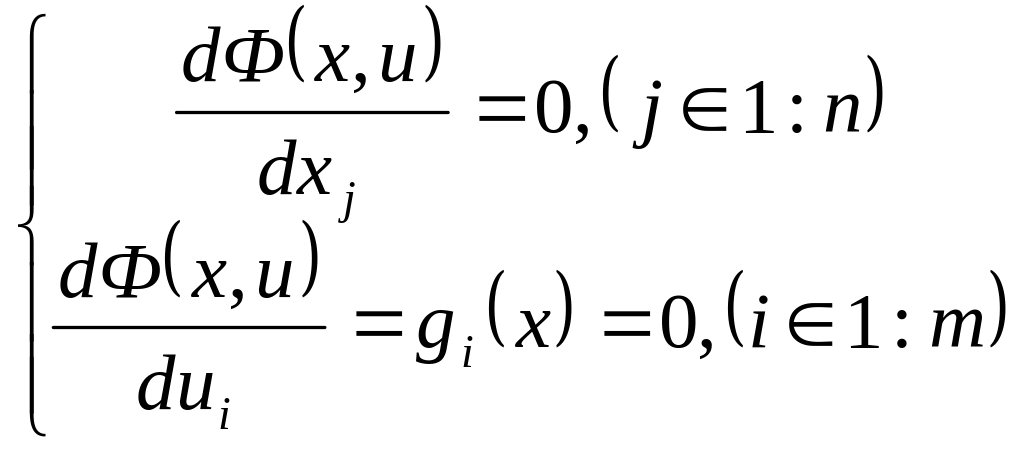
відносно змінних х і и.

При рішенні конкретних практичних задач використовуються прямі методи , що основані на ітеративних процесах обчислення і порівняння значень оптимізаційних функцій.

Приклад 7.2.1

Хай є потреба визначити максимум цільової функції двох змінних: при обмеженнях:

- збудуємо функцію Лагранжа:

- знайдемо частні похідні цієї функції за усіма аргументами і дорівняємо їх 0 (шукаємо критичні точки).

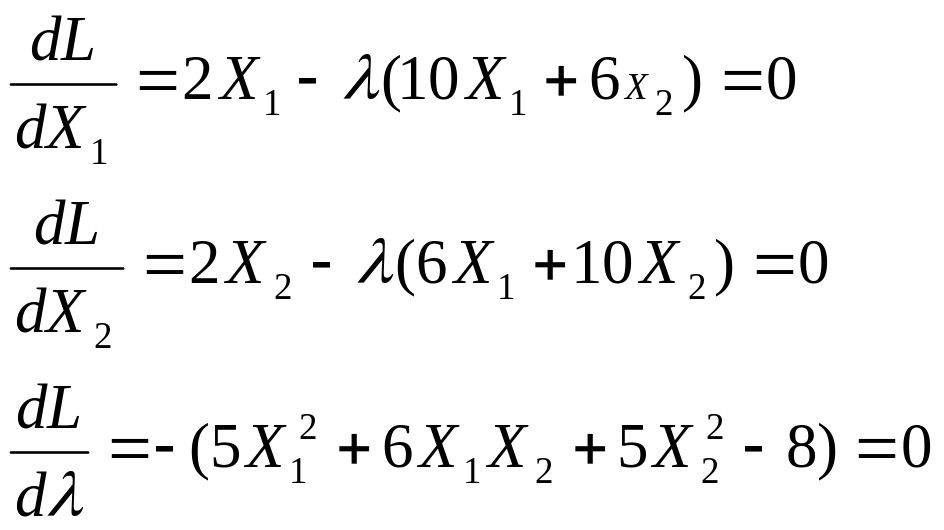
Помножимо 1-е рівняння на Х₂, а 2-е на Х₁ і відрахуємо одне із другого, отримаємо рівняння Звідси витікає, що , або У підсумку отримаємо дві умови для критичних точок: Х₁ = -Х₂. Підставимо по черзі ці рівності у треттє рівняння, отримаємо, що необхідними умовами екстремуму цільової функції є такі: або або . Підстанова цих величин у цільову функцію дає мінімальне значення цієї функції: , що досягається у точках і її максимальне значення , яке досягається в точках .

Цю задачу нелінійних програм можна розглядати як геометричну задачу відшукування найменшої і найбільшої відстані від початку координат лінії другого порядку (еліпсу) у декартовій системі координат: .

Градіентні методи рішення задач безумовної оптимізації

Ці методи займають ведуче місце серед методів рішення екстремальних задач. Нагадаємо, що стаціонарною будемо звати точку де і яка у відповідності із необхідною умовою оптимальності є подізрюючою на наявність локального екстримуму. Ідея даного методу заснована на тому, що градієнт функції вказує напрям її найбільш швидкого зростаня в межах тієї точки де він обчислен. Тому, якщо із деякої точки х⁽¹⁾ зміщується у напрямку вектору , то функція f буде зростати у деякій окрузі х⁽¹⁾. Тобто, для точки , що розміщується у окрузі де справедлива нерівність f(x⁽¹⁾) ≤ f(x⁽²⁾).

Зауважимо як тільки визначається напрямок просування відразу стає питання щодо відстані якої слід просуватись в цьому напрямі, тобто виникає проблема обрання кроку λ у рекурентній формулі: х^(q+1)=x^(q)+λ f(x^(q)), що задає послідовність точок, які спрямовані до точки максимуму.

Із варіантів методу градієнтного рішення найбільш поширеними можна вважати :

а). Метод найскорішого спускання. Назва використовується при вирішення задач на максимум. Хай f(x) = f( x₁, x₂,…, x_n) – диференціруєма функція, що задана на Rⁿ, а х^(q) = (x₁^(q),x₂^(q),….,x_n^(q)) – деяка тікуча точка. Щоб досягти найбільшого із можливих значень f у разі просування у напрямку , потрібно обрати таке значення λ, яке максимізує функцію . Для розрахунку λ використовується необхідна умова екстремуму df(λ)/dλ = 0.

в). Метод подрібнення кроку. Для знаходження кроку λ у методі най скорішого спуску потрібно вирішити рівняння , яке може бути досить складним. Тому найчастіше обмежуються „підбором” такого значення λ , що f(λ) > f(0). Для цього задається деяке початкове значення λ₁ (наприклад, λ₁=1) і перевіряють умови f(λ₁)>f(0). Якщо таке не виконується, то вважають λ₂ = 1∙λ₁/2 і т.д до тих пір доки не знайдено відповідний крок з яким переходять до наступної точки х^(q+1).

Двоїстість у нелінійному програмуванні

Звернемо увагу, що відправною точкою нелінійного програмування вважається застосування методу Лагранжа для вирішення задач із обмеженнями у формі нерівностей:

f(x)→max, D={x X|g_i(x₁,x₂,…,x_n)≤0, i 1:m}, (7.3), де: Х - деяка область у просторі Rⁿ. За аналогією п.2.1.2 визначимо для (7.3) функцію Лагранжа: ,(7.4). Двійка векторів зветься сідловою точкою функції Ф(х,и) у деякій області X×U, якщо для будь-яких і , (7.5). Таку нерівність також звуть нерівністю сідлової точки. Як приклад сідлової точки може бути наведена точка (0,0) для функції Ф(х,и) = - х²+и² визначеної на множині R × R. Дійсно, Ф(0,0) = 0, Ф(х,0) = - х², Ф(0, и) = х², а для будь-яких і виконується умова нерівності –х² ≤ 0 і 0 ≤ u².

У теорії нелінійного програмування центральне місце займає теорема Куна-Таккера, що зв’язує рішення ЗНП із наявністю сідлової точки у відповідній функції Лагранжа (з максимізацією цієї функції по х і мінімізацією по и). Сутність теореми закладена у двох положеннях (теоремах): теорема достатності умови екстремуму і теорема необхідності умови наявності екстремуму.

1. Якщо - сідлові точки функції Лагранжа в області , то є оптимальним планом задачі (7.3), при чому слушно так зване правило доповнюючої нежорсткості.

Твердження зворотне висловленому, тобто необхідна умова екстремуму у ЗНП стає вірним лише за умов виконання додаткових умов, яким повинен задовольняти задача (7.3). Важливішим з них є так звана умова регулярності Слейтера - „Функція g(x), що задає обмеження в задачі (7.3) задовольняє умові регулярності Слейтера, якщо існує така точка , що належить області припустимих планів D і що ” тобто є внутрішньою точкою відносно обмеження g_i(x).

2. Якщо (D, f) є задачею опуклого програмування із рішенням , її цільова функція f(x) і функція обмежень g(x) – диференціруємі, нелінійне обмеження у формі нерівності задовольняють умові регулярності Слейтера, то існує такий вектор , що - сідлова точка функції Лагранжа Ф(х,и). Визначимо F(x) як функцію, що ставить у відповідність кожному значенню х мінімальне значення функції Ф(х,и) по и: і за аналогією . Розглянемо задачу відшукування максимуму функції F(x): , (7.6) і задачу мінімізації G(u): , (7.7). Вочевидь, що . Звідси витікає, що максимум F(х) відшукується у припустимій області D і співпадає із максимумом цільової функції f(x) задачі (7.3): . Таким чином задача (7.6) рівноцінна (7.3). Аналогічні висновки можуть бути отримані і для (7.7). Задачі (7.6) і (7.7) створюють двоїсту пару. Тобто таке відношення є узагальненим відношенням двоїстості для задач лінійного програмування.

Таким чином, при визначених умовах пара двоїстих задач нелінійного програмування має властивості двоїстих лінійних задач. Тобто при будь-яких F(x) ≤ G(u). Ця умова часто застосовуєься при побудові оцінок у ітеративних методах рішення оптимізаційних задач. Наприклад, якщо є можливість приблизно вирішити пряму і двоїсту задачі і отримати послідовності наближень і , то за допомогою нерівностей виду можна визначити термін закінчення розрахункової процедури. Слід зауважити, що у процесі формування нелінійних двоїстих задач існує велика неоднозначність: їх вигляд можна варіювати якщо включати до множини Х частину обмежень g_i(x) ≤ 0.

Матеріали до самоперевірки знань і контролю

Контрольні питання

1. При яких умовах оптимізаційна задача може вважатись нелінійною?

2. Наведіть приклад економічної моделі, що може бути зведена до задачі нелінійного програмування.

3. Перелічите основні труднощі, що виникають в процесі рішення задачі нелінійного програмування.

4. Який сенс вкладається у поняття „умовна оптимізація”?

5. Для чого використовується метод множників Лагранжа і в чому його сенс?

6. Яка точка зветься стаціонарною?

7. Для вирішення яких задач застосовується метод найшвидшого спуску і метод подрібнення кроку?

8. Надайте визначення опуклої (вогнутої) функції.

9. В чому специфіка задач опуклого програмування?

10. Надайте визначення сідловій точці. Наведіть приклад функції, що має сідлову точку.

11. Яка умова отримала назву „правила доповнюючої нежорсткості”

12. Сформулюйте необхідні і достатні умови теореми Куна-Таккера. Яке значення вони мають для рішення задач нелінійного програмування?

13. Сформулюйте задачу яка повинна бути вирішена при визначення кроку у методі припустимих спрямувань.

14. Виходячи із яких міркувань визначається припустимий прогресивний напрям?

15. Наведіть приклад пари двоїстих задач нелінійного програмування.

16. Які властивості пари нелінійних двоїстих задач можуть бути застосовані для їх вирішення?.

Б і б л і о г р а ф і я

1. Абрамов Л.М., Капустин В.Ф. Математическое пограмирование. Л.: 1981

2. Ашманов С.А. Линейное программироание. М.: 1981.

3. Левин Г.М., Танаев В.С. Декомпозиционные методы оптимизации проектных решений. – Л.: Наука и техника, 1978. -240 с.

4. Кросс М.С., Чупрынов Б.П. Основы математики и ее приложений в экономическом образовании. Ч.2.Основы оптимального управления. М.:ДЕПО, 2001.

5. Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: "BHV – CПб", 1997. – 384 с.

5. Трояновский В.М. Математическое моделирование в менеджменте. – М., 2002. – 252 с.