7.2.1. Динамічне програмування (узагальнені процедури методів)

Метод вважається оптимізаційним, що орієнтований на вирішення задач які виникають у разі вибору найкращої послідовності прийняття управляючих рішень.

В основу метода покладено принцип оптимальності Беллмана [2,3]: «Оптимальна стратегія має таку особливість, що якими б не були початкові стани системи і наслідки раніше прийнятих відносно неї рішень, не подальші дії повинні складати оптимальну стратегію, що виходить із стану системы, яке є результатом попередніх рішень». Тут використана математична ідея рекурсії.

Є сенс розглянути основні процедури динамічного програмування на прикладі дискретних детермінованих багатокрокових процесів прийняття рішень. Дискретним будемо називати процес, де рішення (перетворення) відбувається кінцеве або безкінцеве, але лічильну кількість разів. Детермінованим є процес в якому для заданого початкового стану Р вибір рішення q єдиним чином визначає перетворення T(H,q).

Хай у початковому стані Р₁ обирається початкове рішення q₁ у результаті чого система переходить в новий стан Р₂, що можна визначити як Р₂ = Т(Р₁, q₁); (7.8) в стані Р₂ застосовується друге рішення q₂, що переводить систему у новий стан Р₃ = Т(Р₂,q₂). Процес продовжується таким чином і Р_N для деякого довільного N знаходиться із співвідношення Р_N = T(P_N-1, q_N-1).

Виникає запитання, на чому грунтується вибір q_i? Розглянемо це питання для випадку, коли N – кінцеве число. Такий процес звуть N-кроковим. Зв’яжемо із N-кроковим процесом скалярну функцію

F(P₁, P₂,…,P _N; q₁, q₂,…,q_N); (7.9). Ця функція має назву критеріальної.

Припустимо, що мета процесу прийняття рішення – обрати q_i таким чином, щоб максимізувати цю функцію за Р_і і q_i. Для конкретизації процесу розглянемо задачу максимізації функції: F = g(P₁,q₁)+g(P₂,q₂) = …+ g(P_N, q_N), (7.10) за всіма q_i, де як і раніше, Р_і = Т(Р_і-1,q_i-1), I = 2,3,..,N.

Припустимо, що максимум існує, а q_і приймає лише кінцеве число значень і що функція g(P,q) приймає кінцеві значення для усіх кінцевих H і q.

Основна ідея динамічного програмування тут полягає в тому, що замість того щоб розглядати поставлену задачу для фіксованих Р ізольовано, вона включається у комплекс процесів максимізації. Передбачаємо, що значення Р_і належить деякій області, а N приймає значення 1,2..., створимо послідовність функцій f_N(P_i) = max[g(P₁,q₁)+g(P₂,q₂)+,…,g(P_N,q_N)], (7.11).

Зауважимо, що функція f₁(P₁) відшукується відносно легко. Для цього потрібно, як витікає з відношення , лише вирішити найпростішу із поставлених вище задачу, оскільки максимізація повинна проводитись лише по одній змінній q₁. Далі треба отримати співвідношення, що пов'язує різні елементи послідовності {f_N(P₁)}. Запишимо: , (7.12.). Адитивність критерію дозволяє записати це співвідношення у такому вигляді: . (7.13)

Є сенс розглянути вираз , (7.13), де: N≥2. Вираз (7.13) – величина критерію, що отримується у (N-1)-кроковому процесі прийняття рішень, який починається із стану Р₂. Звідси маємо співвідношення: , (7.14). Використовуючи (7.14) можна суттєво спростити вираз (7.13) і надати йому вигляд: , (7.15), або оскільки Р₂ = Т(Р₁,q₁) , (7.16). Формула (7.16) зв’язує різні члени послідовності {f_N(P₁)}. Такий же результат можна отримати по-іншому за допомогою принципу оптимальності. Введемо необхідні поняття: стратегія – послідовність припустимих рішень {q₁,q₂,…,q_N} у випадку N-

крокових стратегій; оптимальна стратегія - стратегія, що доставляє максимальне значення функції. Основна властивість оптимальних стратегій виражається таким принципом оптимальності. Оптимальна стратегія має таку властивість, що яке б не було початкове становище і початкове рішення, наступні рішення повинні складати оптимальну стратегію відносно стану, що є результатом застосування першого рішення.

Використовуючи принцип оптимальності, можна отримати рекурентне співвідношення (7.16) на підставі логічних міркувань. Припустимо, що ми приймаємо деяке початкове рішення q₁, у (N-1) – кроковий.

Відповідно до принципу оптимальності частка максимального значення критерія від залишків (N-1) кроків буде f_N-1(T(P₁,q₁). Таким чином для деякого q₁ маємо f_N(P₁) = g(P₁,q₁) = f_N-1(T(P₁,q₁)). (7.17). Очевидь, q₁ повинно бути обрано так, щоб максимізувати праву частину (7.17). У результаті підсумкове рівняння має вигляд: , (7.18). Помітимо, що звичайний підхід до задачі максимізації веде до рішенню у формі [q₁,q₂,…, q_N], тобто у формі, яка отримується в результаті варіаційного процесу. Метод динамічного програмування дає це рішення послідовно: на першому кроці – вибір q₁, потім вибір q₂ і т.д.

Тобто однократне рішення складної задачі замінюється багатократним рішенням простих. Важливо, що значення критерію – сума частих значень, що отримані на окремих кроках і передумови не мають значення при визначенні майбутніх дій.

У спрощенному випадку рішення задачі динамічного програмування записується таким чином [10 ].

Припустимо наявність n функцій з невід’ємним значенням f₁(x₁), x₁ d₁,…,f_n(x_n), x_n d_n, де d_1,…., d_n- область визначення змінних. Треба знайти максимум (або мінімум) F(x₁,…,x_n) = f₁(x₁) +…+f_n(x_n) при будь-яких обмеженнях на змінні х₁,...,х_n. У простішому випадку обмеження одне х₁+ х₂+...+х_n = A. Схема дій буде такою: знайти , потім і т.д, а в кінці .

Приклад 7.2.2

Хай фірма має три торгівельні точки і об’єм капіталу в умовних одиницях. Менеджменту фірми відомі залежності прибутку по кожній точці від об’єму вкладень визначеного капіталу у цю точку (табл.7.17)

Таблиця 7.17 Ісходні дані

Вкладення	1	2	3
0	0	0	0
1	0,25	0,25	0,15
2	0,45	0,41	0,25
3	0,65	0,55	0,40
4	0,76	0,65	0,50
5	0,90	0,75	0,62
6	1,02	0,80	0,73
7	1,13	0,85	0,82
8	1,23	0,88	0,90
9	1,32	0,90	0,96

Як скористатись капіталом, щоб отримати максимальний прибуток? Зрозуміло, що можна розглядати усі можливі комбінації розподілення капіталу, наприклад, при 4-х одиницях капіталу: (4,0,0), (0,4,0), (0,0,4); (3,1,0), (3,0,1); (2,2,0), (2,0,2), (2,1,1) і т.д.

Для вирішення задачі введемо означення: f₁(x), f₂(x), f₃(x) - функції прибутку в залежності від вкладень, тобто є стовпці 2-4 табл. 7.18 - F₁₂ (A) - оптимальне розподілення, коли А одиниць капіталу вкладаються у першу і другу торгові точки разом, F₁₂₃(А) – оптимальне розподілення капіталу величини А, що вкладається в усі точки разом.

Наприклад, для визначення F₁₂(2) треба знайти f₁(0) + f₂(2)=0,41, f₁(1)+f₂(1) = 0,53, f₁(2)+ f₂(0) = 0,45 і обрати з них максимальну, тобто F₁₂(2) = 0,53. У загальному вигляді: F₁₂(A) = max [f₁(x)+ f₂(A-x)]. Розраховуємо F₁₂ (0), F₁₂(1), F₁₂(2),…,F₁₂(9), які заносимо до табл..7.18.

Вкладення (А)	f1(x)	f2(x)	F12(A)	Оптимальне розподілення
0	0	0	0	0,0
1	0,28	0,25	0,28	1,0
2	0,45	0,41	0,53	1,1
3	0,65	0,55	0,70	2,1
4	0,78	0,65	0,90	3,1
5	0,90	0,75	1,06	3,2
6	1,02	0,80	1,20	3,3
7	1,13	0,85	1,33	4,3
8	1,23	0,88	1,45	5,3
9	1,32	0,90	1,57	6,3

Таблиця 7.18. Функції прибутку від вкладень

Для А=4 можливі комбінації (4,0), (3,1), (2,2), (1,3), (0,4), які дають відповідно загальний прибуток: 0,78; 0,90; 0,86; 0,83; 0,65. Більш детально отримання цих значень показано у формальному вигляді:

F₁₂ = max {f₁(x) + f₂(F-x)};

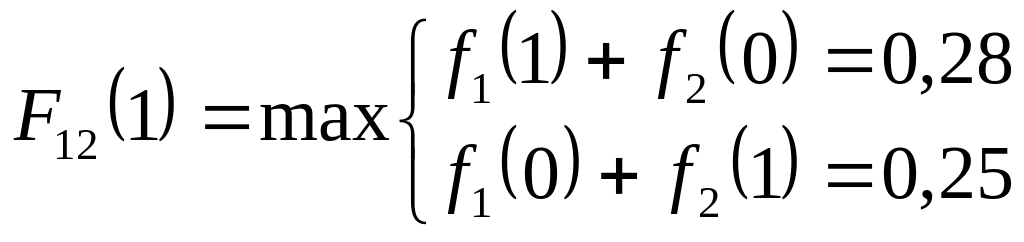
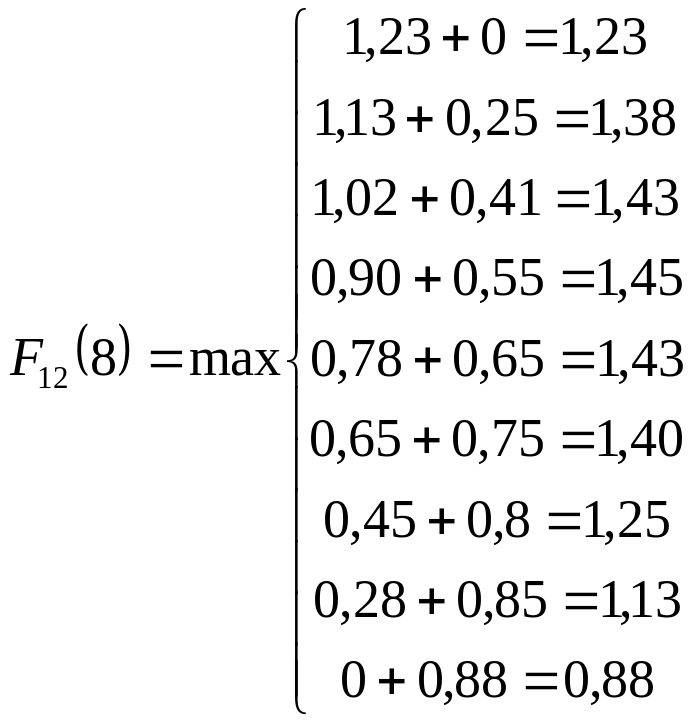
Якщо ми маємо залежність F₁₂ від величини капіталу, що вкладається у перші дві точки, можна шукати F₁₂₃(A) = max [F₁₂(x)+f₃(A-x)]. Результати наведемо у табличній формі (табл..7.19):

Таблиця 7.19. Розподілення капіталу між трьома точками

Вкладення (А)	F12(x)	f3(x)	F123(A)	Оптимальне розподілення
0	0	0	0	(0,0,0)
1	0,28	0,15	0,28	(1,0,0)
2	0,53	0,25	0,53	(1,1,0)
3	0,70	0,40	0,70	(2,1,0)
4	0,90	0,50	0,90	(3,1,0)
5	1,06	0,62	1,06	(3,2,0)
6	1,20	0,73	1,21	(3,2,1)
7	1,33	0,82	1,35	(3,3,1)
8	1,45	0,90	1,48	(4,3,1)
9	1,57	0,96	1,60	(5,3,1) або (3,3,3)

Більш детально процедури отримання даних стосовно ефективності вкладання капіталу у три торгівельні точки для дев’яти одиниць наведено в табл.. 7.20.

Таблиця 7.20 Розподілення 9 одиниць капіталу

Капітал	х1+х2	х3	F123
9	9	0	1,57
	8	1	1,45+0,15= 1,6 (5,3,1)
	7	2	1,33+0,25=1,58
	6	3	1,2+0,4=1,6 (3,3,3)
	5	4	1,06 =0,5=1,56
	4	5	0,9+0,62=1,52
	3	6	0,7+0,73=1,43
	2	7	0,53+0,82=1,35
	1	8	0,28+0,90=1,18
	0	9	0,96

Важливо те, що отримані результати були б тими ж, якщо використовувались не F₁₂ і F₁₂₃ а скажімо F₃₁ і F₃₁₂ . Зверніть увагу, що оптимальне рішення для А=9 – не єдине.

Приклад 7.2.3

Нехай маємо мережу міст (О) і доріг (→). Знайти оптимальний шлях від міста А до міста D.

Рисунок 7.7. Мережний графік маршрутів

Дифініції щодо терменів: Стан системи – конфігурації системи (факт знаходження у конкретному місті); Крок – перехід системи із одного стану до іншого ( суміжне з ним); Стратегія – комплекс дій спрямованих на досягнення мети як вибір маршруту, наприклад: А→ B₂→ C₂ → D, або A→ B₄ → C₁→ D.

Задача вирішується у два етапи.

6

Рисунок 7.8 Формалізована схема пересування

Означення на рис.7.8:

О – міста;

→ - відстань між містами.

На 1-му етапі будується рекурентне співвідношення, що пов’язується між собою різними кроками.

На 2-му береться до уваги вказане співвідношення і відбувається розрахункова процедура з метою вибору оптимального рішення.

Для спрощення обчислення вводяться змінні кроку стану:

• n - число рубіжних кроків, i – стан на кожному кроці;

• побудувавши рекурентне співвідношення визначимо;

• мінімальну відстань від міста (0,1), тобто А, до міста (n, i), а 2(n-1,j : n,1) – як відстань від міста (n-1,J) до міста (n, i). Так, 2 (1,1: 2,2) в задачі становитиме 8 км.

Відповідно із принципом оптимальності, будуємо рекурентне співвідношення:

де за визначенням

Шляхом багаторазового використання виразу можна отримати таке:

Крок 1:

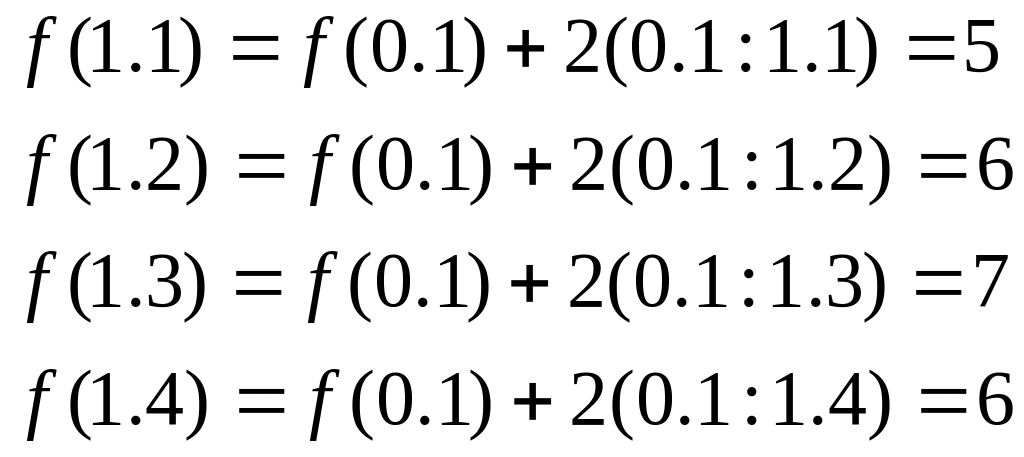
Крок 2:

Таким чином

Аналогічно

Крок 3

Таким чином: .

Мінімальна відстань від міста (0,1) до міста (3,1) = 14км., а оптимальний маршрут визначається за допомогою зворотної підстанови, а саме:

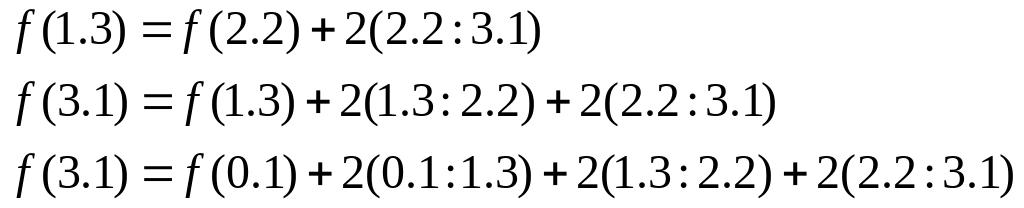
Оптимальною стратегією є маршрут: місто місто місто місто (3,1), тобто - .

Звернемо увагу та те, що ми пересувались з ісходного стану лише вперед. Така організація процесу зветься прямим рекурентним співвідношенням, або динамічним програмуванням із прямою ходою в часі. Задачу можна вирішувати і з допомогою зворотного рекурентного співвідношення. При цьому обчислювальна процедура буде більш економічною.

Динамічні задачі управління запасами

Приклад 7.2.4

Хай маємо систему постачання, що планує роботу на n періодів. Основна діяльність фірми-постачальника зводиться до забезпечення попиту кінцевих споживачів на продукт. Для цього вона робить замовлення виробнику цього продукту. Попит споживачів продукту будемо розглядати як інтегровану величину, що приймає задані значення для кожного з періодів і попит повинен завжди задовольняться (відсутні борги і відмови). Також передбачається, що замовлення виробнику задовольняється ним в повній мірі і часом між замовленням і виконанням зневажаємо (система з миттєвим виконанням замовлення). Вводимо означення:

У_k – залишок запасу після (k-1)-го періоду;

d_k – заздалегідь відомий сумарний попит у k-му періоді;

x_k – замовлення (постачання від виробника) у k-му періоді;

с_k(x_k) – витрати на виконання замовлення об’єму x_k у k – му періоді;

s_k(h_k) – витрати на збереження запасу об’ємом h у k –му періоді.

Після отримання поставки і задовольнення попиту об’єм товару, що підлягає зберіганню у період k, становить: h_k = y_k+x_k - d_k. Враховуючи сенс параметра у_k, можна записати сіввідношення: h_k = h_k-1+x_k – d_k, k 2/n.(7.19). Витрати на отриманні і збереження товару в період k описуються функцією:

F_k(x_k, h_k) = c_k(x_k)+s_k(h_k), k 1/n.

Планом задачі можна вважати вектор х = (х₁,х₂,...,х_n), компонентами якого є послідовні замовлення у продовж проміжку часу, що розглядається. Співвідношення між запасами (7.19) у сполученні з деяким початковими умовами зв’язує стан системи із обраним планом і дозволяє виразити сумарні витрати за всі n періодів функціонування керуємої системи постачання у формі адитивної цільової функції: , (7.20). Природним в межах сформованої моделі є задача пошуку послідовності оптимальних управлінь (замовлень) і пов’язаних з ними оптимальних станів (запасів) , які повертають у min (7.20). У якості первинної умови використаємо вимогу про збереження після завершення управління заданої кількості товару у_n+1, а саме (7.21). При вирішенні поставленої задачі методом динамічного програмування у якості функції стану керуємой системи A_k(h) логічно узяти мінімальний об’єм витрат, що виникають за перші k періоди при умові, що в k-й період має запас h. В такому разі можна записати основне рекурентне відношення: , , (7.22.) оскільки у_k= h-x_k + d_k > 0, і , (7.23).

Система рекурентних співвідношень (7.22) – (7.23) дозволяють знайти послідовність функцій стану А₁(h), A₂(h),…,A_n(h) і умовних оптимальних управлінь , . На n-му кроці на підставі початкової умови (7.21) можна визначити . Інші значення оптимальних керувань визначаються за формулою: , (7.24). Цікавим є випадок задачі (7.19) – (7.20) при якому передбачається, що функції витрат на поповнення запасу с_k(x_k) є вгнутими по х_k, а функції витрат на збереження s_k(h_k) є лінійними відношеннями об’єму запасу, що зберігається, тобто s_k(h_k) = s_kh_r. Означимо функцію витрат у продовж k-го періоду як

f_k(x_k, h_k) = c_k(x_k)+s_kh_k, (7.25), або теж саме, f_k(x_k, y_k+1) ₌ c_k(x_k) + s_ky_k+1, (7.26).

Враховуючи зроблені пропозиції усі функції витрат f_k(x_k, y_k+1) є вгнутими. Така властивість значно спрощує процес рішення, оскільки для пошуку мінімуму вгнутих функцій f_k(x_k, y_k+1) досить розглянути лише дві граничні точки множини, на якому відшукується мінімум.

Із врахуванням введеного означення задачу (7.19)–(7.20) можна записати у вигляді: , (7.27) при умовах х_k + y_k – y_k+1 = d_k; k 1:n, (7.28).

Розглянемо процедуру рішення (7.27) – (7.28). Оскільки відшукується мінімум суми вгнутих функцій f_k(x_k, y_k+1), то рішення буде досягнуто на одній із граничних точок множини, що визначається умовою (7.28). Загальне число змінних х_k і y_k в системі (7.28) дорівнює 2n. Однак враховуючи те, що у неї лише n рівнянь, в оптимальному плані буде не більше n не нульових компонент, при чому для кожного періоду k значення х_k і y_k не можуть дорівнювати нулю одночасно. Формально це ствердження можна навести у вигляді умови, додаючи не жорсткості: , (7.29), де: (7.30). З точки зору змістовної інтерпретації умови (7.29) – (7.30) означає, що у разі оптимального управління замовлення постачальнику на наступну партію не повинне надходити, якщо на початку періоду є не нульовий запас, або розмір замовлення повинен дорівнювати величині попиту на ціле число періодів. Звідки слідує, що запас на кінець останього періоду повинен дорівнювати нулю: . Останнє дозволяє вирішити задачу у прямому спрямуванні, застосувавши рекурентне співвідношення , (7.31), де: h = y_k+1= x_k + y_k - d_k. Враховуючи (7.29) – (7.30) і вгнутість f_k(x_k, h) робимо висновок, що мінімум (7.31) досягається у одній із граничних точок x_k = 0 або х_л = h + d_k, тому 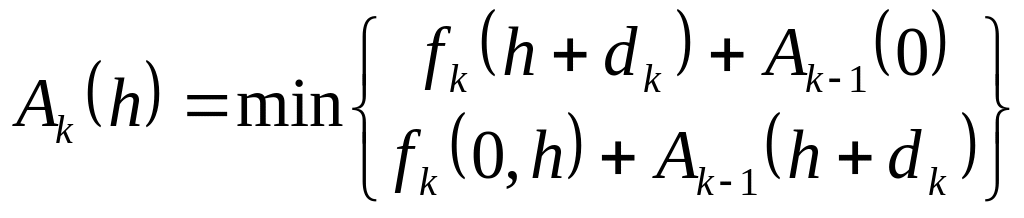, (7.32). В такому разі для попереднього періоду функція стану може мати вираз , (7.33) на підставі чого у загальному вигляді отримуємо модіфіковану форму для рекурентного співвідношення: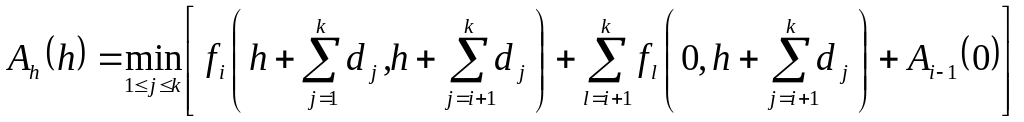 , (7.34). При подальших конкретизуючих передбаченнях щодо виду функцій f_k(x_r, y_k+1), можна отримати ще більш компактні форми для рекурентних співвідношень.

Наведені перетворення ілюструють загальні підходи, що застосовуються в динамічному програмуванні, а також ті властивості задач, які віддзеркалюють можливості для ефективного використання методу в прикладному операційному менеджменті.

Постанова і рішення задачі щодо використання робочої сили

Враховуючи важливість проблеми управління робочою силою, організація цілеспрямовано опікується проблемою ефективності використання цього фактору.

Приклад 7.2.5

Функціонує організація у продовж кінцевого числа періодів k (k 1: n). Кожний період k характеризується нормативною потребою у визначеної кількості одно профільних робітників m_k. Той же об’єм робіт може бути виконано іншою групою персоналу у кількості h_k, але це збільшує витрати. Величина додаткових витрат можна описати функціями g_k(h_k - m_k), де (h_k – m_k) – відхилення фактичної чисельності робітників h_k віл планово необхідного m_k, при цьому g_k(0)=0. Управляюче рішення на кроці k полягає у виборі величини зміни числа персоналу , що визначає кількість працюючих у продовж періоду : h_k+1 =h_k+x_k. Витрати на зміну кількості робітників (наймання, звільнення) у разі переходу від періоду k до періоду (k+1) задаються функцією u_k(x_k), де також u_k(0) = 0. У такому випадку сумарні витрати, що викликані прийнятим на кроці k рішенням характеризуються значенням функції: f_k (x_k,h_k) = g_k(h_k- m_k) + u_k(x_k), x_k ≥ - h_k.

Стратегія управління (план задачі) x= (x₁,…,x_k-1 , 0) полягає у виборі поетапної зміни кількості робітників, а його сумарна ефективність описується адитивною функцією , (7.35), де: h_k=h_k-1+x_k-1, k>1. На основі сформульованої моделі ставиться задача мінімізації цільової функції (витрат) - (7.35). Додамо, що постанова задачі не буде коректною, якщо не задати початкові умови на кількість робітників. Існує дві модифікації задачі, що визначається типом початкової умови: у першому випадку задається ісходне значення на першому етапі m₁, а в іншому – потрібна кількість у n-му періоді m_n.

Розглянемо перший випадок. Оскільки початкова кількість робітників є фіксованим, але нічого невідомо про те яким ця кількість повинна буде на кінцевому етапі, то розглядати процес прийняття рішення зручно з кінця. Оптимальне управління на останньому етапі n за умов дорівнює , тому мінімальні витрати в повній мірі визначаються кількістю робітників в останньому періоді: А_n(h)=f_n(0,h)= g_n(h – m_n), h≥0, (7.36). Для інших передуючих кроків основне рекурентне співвідношення прийме вигляд: , (7.37) , де: A_k(h) – мінімальні витрати з k-го до n-й періоди у припущенні, що кількість робітників у k-й період дорівнює h. Точки , в яких досягаються мінімуми (7.37) визначають умовне оптимальне управління на кожному кроці. Послідовно визначаючи і дійшовши до етапу 1, ми зможемо знайти безумовне оптимальне управління з тієї умови, що початок першого періоду - чисельність робітників повинна становити , а саме: Інші компоненти оптимального плану і стану , що створюють оптимальну траєкторію, послідовно знаходяться за рекурентними формулами: після чого не вважається важким обрахувати оптимальне значення цільової функції (7.35).

Розглянемо другий випадок, коли задано фінальний стан об’єкту, тобто бажану кількість робітників на останньому періоді . Вочевидь, що у даному випадку слід поступати із точністю до „навпаки” і розглядати процес прийняття рішень від початку до кінця. Найкраще умовне управління на першому кроці буде знайдене у процесі обчислення функції: , (7.38), де: h ≥ 0 є можливою кількістю робітників на початковому кроці. Відповідно, основне рекурентне співвідношення відобразить мінімальні витрати до k-го періоду через такі для попередніх періодів (з 1-го до k-1) при умові, що чисельність робітників у k-й період буде дорівнювати h: . (7.39). Побіжно будуть знайдені функції , , що визначають умовні оптимальні рішення. В останньому періоді на підставі початкової умови, . Звідси шляхом послідовного рішення рекурентних рівнянь можуть бути знайдені оптимальна кількість робітників і безумовні оптимальні управління: . У підсумку, як і в першому випадку підраховуються мінімальні значення витрат.

Узагальнюючи наведені процедурні схеми рішення можна прийти висновку: При використанні алгоритмів динамічного програмування, якщо задано початковий стан системи, що управляється, то задача вирішується у зворотному напрямку, а якщо кінцевий, то – у прямому. Якщо задані як початкові так і кінцеві стани, то задача значно ускладнюється (компромісом може бути відмова від оптимізації на першому або останньому етапах).

Числове наповнення прикладу 7.2.5

Фірмі у продовж 4-х місяців за нормативами потрібні робітники однакової кваліфікації: m₁ = 3, m₂ =4, m₃ =5, m₄ =2, при цьому, на початку першого місяця (нульовий місяць) фактично маємо h₀=2 робітника.

Адміністрація планує в кінці кожного місяця k (за виключенням останнього) коректувати чисельність робітників на величину х_k, k , х₄=0. На наймання одного робітника витрачається $9, на звільнення -$6. Передбачається, що витрати на зайвого робітника складуть $8,а у випадку недостатності робітників витрати сягатимуть $12 на кожне вакантне місце. Знайти оптимальні значення прирощення чисельності робітників на кінець кожного із перших трьох місяців при яких сумарні витрати у продовж всього періоду, що розглядається, будуть мінімальні.

На початку процедур вирішення запишемо в аналітичній формі функції витрат на процедури наймання-звільнення робітників (и), а також на утримання поза нормативного штату (g). Для цього вводимо функції:

(7.40)/ (7.41) .

Оцінка ефективності на кожному кроці має вигляд: . Оскільки у поставленої задачі надається початкова умова , її рішення починається з кінця і як слідство застосовуються рекурентні співвідношення (7.37). З технічної точки зору зручним буде на кожному кроці складати дві таблиці значень: функції витрат, що отримані починаючи із поточного кроку в залежності від поточного стану і управління Ω_k(f_k(x_k,h)+A_k+1(h+x_k), (7.42) і функції мінімальних витрат у залежності від поточного стану , (7.43). Для скорочення об'єму тубулючих значень можна скористатись властивостями опуклості функції Ω_k(x_k,h), що витікають із опуклості f i g. Із опуклості функцій Ω_k(x_k,h) отримуємо, що заповнювати таблицю її значень потрібно лише до тих пір, поки вони зменшуються, тобто можна зупинитись, як тільки чергове значення оказується більшим за попереднє. Помітимо, що такі операції є поширеними у динамічному програмуванні. Зрозуміло, що методи які нами ілюструються не розраховані на ручний процедурний режим, оскільки пов’язані із значним об’ємом рутинних обчислень, але надають цілком достатнє уявлення про сутність методу і можливості його використання. Заради скорочення наводимо лише фрагменти таблиць, що ілюструють значення які нас цікавлять.

Ітерація 1. Вважаємо k = 4. На даному етапі функція стану A₄(h) може бути знайденою безпосередньо, якщо враховувати, що і u(0) = 0:

.

Таблиця значень цієї функції і умови оптимальності управління мають вигляд:

h	0	1	2	3	4	5	6
A4(h)	24	12	0	8	16	24	32
	0	0	0	0	0	0	0

Ітерація 2. Вважаємо k = 3. Спочатку заповнимо таблицю значень функції Ω₃(х₃, h) для достатньо великої множини аргументів відповідно з формулою: Ω₃(x₃, h)=f₃(x₃, h)+A₄(h+x₃) = u(x₃)+g(h-5)+A₄(h+x₃)

h	0			1			2			3			4			5
x3	1	2	3	0	1	2	-1	0	1	-2	-1	0	-3	-2	-1	-4	-3	-2
f3(x3,h)	69	78	87	48	57	66	42	36	45	36	30	24	30	24	18	24	18	12
A4(h+x3)	12	0	8	12	0	8	12	0	8	12	0	8	12	0	8	12	0	8
Ω3(x3,h)	81	78	95	60	57	74	54	36	53	48	30	32	42	24	26	36	18	20

h	0	1	2	3	4	5
A3(h)	78	57	36	30	24	18
	2	1	0	-1	-2	-3

Обираючи мінімальні по х₃ значення Ω₃(х₃, h) сформуємо таблицю A₃(h) і відповідні значення умовних оптимальних стратегій

Ітерація 3. Будемо вважати k = 2. Також як на попередньої ітерації, заповнимо таблицю значень функцій Ω₂(х₂, h) відповідно до формули:

Ω₂(x₂, h)=f₂(x₂, h)+A₃(h+x₂) = u(x₂)+g(h-4)+A₃(h+x₂)

h	0			1			2			3			4			5
X2	1	2	3	0	1	2	-1	0	1	-1	0	1	-1	0	1	-1	0	1
f2(x2,h)	57	66	75	36	45	54	30	24	33	18	12	21	6	0	9	14	8	17
A3(h+x2)	57	36	30	57	36	30	57	36	30	36	30	24	30	24	30	24	18	32
Ω2(x2,h)	114	102	106	93	81	84	87	60	63	54	42	45	36	24	27	38	26	49

h	0	1	2	3	4	5
A2(h)	102	81	60	42	24	26
	0	0	0	0	0	0

Обираючи мінімальні по х₂ значення Ω₂(х₂,h), составимо таблицю А₁(h)і відповідні значення умовних оптимальних рівнянь

Ітерація 4. Приймаємо k=1. За аналогією попереднього. Заповнимо таблицю значень функції Ω₁(х₁, h) у відповідності із формулою:

Ω₁(x₁, h)=f₁(x₁, h)+A₂(h+x₁) = u(x₁)+g(h-3)+A₂(h+x₁)

	h				0							1					2				3				4
	х1				3		4			5		2		3		4	1		2	3	0		1	2	-1		0	1
	f1(x1,h)				63		72			81		42		51		60	21		30	39	0		9	18	14		8	17
	A2(h+x1)				42		24			26		42		24		26	42		24	26	42		24	26	42		24	26
	Ω1(x1,h)				105		96			107		84		75		86	63		54	65	42		33	44	56		32	43

h	0	1	2	3	4
A1(h)	96	75	54	33	32
	4	3	2	1	0

Обираючи мінімальні по х₁ значення Ω₁(x₁, h), складемо таблицю A₁(h) і відповідні значення умовних оптимізацій них управлінь

Ітерація 5. На останній ітерації у зв’язку з наявністю початкової умови достатньо визначити Ω₀(x₀, 2)=f₀(x₀, 2)+A₁(2+x₀)= u(x₀)+A₁(2+x₀), x₀≥-2

і знайти як точку мінімуму Ω₀(х₀, 2). Прості перетворення показують, що мінімум досягається при .

Таким чином після чого зворотною ходою послідовно розраховуються оптимальні управління і оптимальний стан (оптимальна троєкторія):

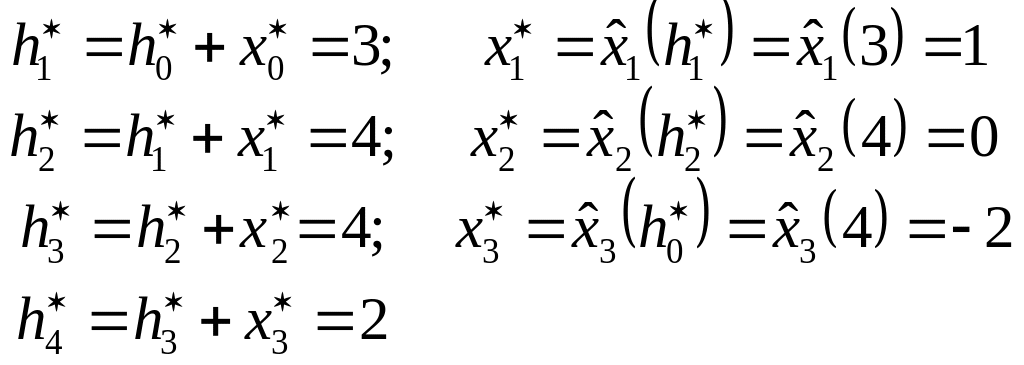Результати розрахунку свідчать, що при заданою системою тарифів у третьому місяці вигідно не запрошувати 5-го робітника, компенсувати його відсутність додатковими виплатами за свехнормовану роботу робітникам які залишаться.

Контрольні запитання

1. Для вирішення яких задач використовують метод динамічного програмування?

2. В чому полягає сутність методу динамічного програмування?

3. Яким умовам повинна задовольняти задача, щоб для її вирішення можна було б застосовувати алгоритм динамічного програмування?

4. Які труднощі пов’язані із обчислювальними алгоритмами динамічного програмування?

5. Що визначає не пряме рішення задачі в алгоритмах динамічного програмування?

6. Запишіть основне рекурентне співвідношення, що використовується при рішенні задачі про наймання робітників

7. З якими особливостями задач управління запасами пов’язано застосування апарату динамічного програмування?

8. Який вигляд має цільова функція у динамічній задачі управління запасами?

9. Запишіть основне рекурентне співвідношення, що використовується при рішенні динамічної задачі управління запасами.

Б і б л і о г р а ф і я

1. Архипова М.И., Кульба В.В., Косяченко С.А., Чанхиева Ф.Ю. Исследование систем управления. Учебн.пособие для вузов. - М.:, изд.ПРИОР, 2002. – 384 с.

2. Беллман Р. Динамическое программирование. –М.:, 1960.

3. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования.- М.:, 1965.

4. Вітлінський В.В. Моделювання економіки. Навч. посібн. - К.: КНЕУ, 2003.- 406 с.

5. Давыдов Э.Г. Исследование операций. Учебн. Пособие для студентов вузов. - М.:, 1990.

6. Канюховский П.В. Математические методы исследования операций в экономике. Учебн. пособие. - СПб: «Питер»; 2000. - 208 с.

7. Карлин С. Математические методы в теории игр, программировании и економике.- М.:, 1964

8. Карманов В.Г. Математическое программирование. - М.:, 1986.

9. Кюнце Г.П., Крелле В. Нелинейное программирование. М., 1965.

10. Монахов А.В. Математические методы анализа экономики. Учебн.рособие. – СПб:, «ПИТЕР», 2002. – 176 с.

11. Оре О. Теория графов. - М.:, 1968.

12. Трояновский В.М. Математическое моделирование в менеджменте. Учебн. пособие.- М.:, РДП, 2002. - 252 с.

13. Фиакко А., Мак-Кормик Г. Нелинейное программирование. Методы последовательной безусловной минимизации. - М.:, 1972.

14. Юдин Д.В., Гольштейн Е.Г. Линейное программирование (теория, методы и приложения).- М.:, 1969.

15. Хедли Дж. Нелинейное и динамическое программирование. - М.:, 1967