8.2.3. Водопонижение при проходке шахтного ствола

Для предотвращения прорыва воды в ствол, вскрывающий на­порный водоносный горизонт, обычно проводят предварительное во­допонижение круговой системой скважин, оборудованных погруж­ными насосами. В таком случае заданными являются расходы сква­жин, отвечающие номинальной производительности насоса (т.е. на скважинах задано граничное условие II рода), а также требуемое по условиям предотвращения прорыва понижение напора на оси ствола S_Q. Используя формулу Тейса (см. раздел 4.1) и принцип сложения течений (см. раздел 3.3), получаем:

^г0

/ о \

„ *

4 at

⁵о(0 ¹ 4 Ж Т ^Ei

(8.12)

где г₀ — радиус круговой установки скважин; п — число скважин.

По формуле (8.12) нетрудно подобрать требуемый водоотлив и число скважин— в зависимости от заданного времени водопониже- ния t. Необходимо только помнить, что выведенная формула спра-

ведлива лишь до тех пор, пока обеспечивается принятый расчетный приток к скважинам, т.е. пока уровень воды в них не упадет до отметки нижнего водоупора. Следовательно, расчет по формуле (8.12) должен сопровождаться дополнительной оценкой понижений в самих скважинах SJS_r < S ):

Ос

⁵с(0 _4лт

(8.13)

. \

пр'

/

предельное понижение уровня в скважине (отвечающее отметке водоупора);

г_с — радиус скважины;

Г{ — расстояние от выбранной расчетной скважины до скважи­ны с номером U

Бели, начиная с некоторого времени t_np, оценка по формуле (8.13) дает S_c(t) > S^, то при t> t_np скважины переходят на режим работы с постоянным уровнем (граничное условие I рода). Такой режим пристволового водопонижения, ориентированного на предот­вращение прерыва через вскрываемый стволом водоупор, обычно следует считать нецелесообразным: он свидетельствует о том, что либо расход насосов, либо число скважин выбраны неудачно.

8.3. Прогноз во^опритоков к открытым горным выработкам

8.3.1. Обцая характеристика прогнозной ситуации

Прогноз водопритоков к открытым выработкам — карьерам, траншеям, котлованам — имеет целью оценку условий их проходки (в частности, оценку влияния подземных вод на устойчивость филь­трующих откосов — см. раздел 8.1), определение необходимости и целесообразных объемов дренажных работ (см. раздел 8.2), а также обоснование мероприятий по охране подземных вод района от исто­щения и загрязнения (см. раздел 8.4).

Вскрытие карьерами или траншеями водоносных горизонтов со­провождается, как правило, существенными нарушениями естест­венного гидродинамического режима вследствие изменений условий разгрузки подземных вод. В то же время усиленное дренирование водоносных горизонтов горными выработками приводит к интенси­фикации их связи со смежными горизонтами, поверхностными водо­емами и водотоками, т.е. к изменению условий питания подземных вод. К тому же при строительстве и эксплуатации крупных карьеров нередко создаются разнообразные гидротехнические сооружения (водохранилища, каналы, а также пщроотвалы, хвостохранилища и

* Раздел написан при участии Ю.А.Норватова.

^Snp ~

V

\

n—1

+2 л,

i — 1

^ri

. *

4 at

. *

4 at

/ J

где

другие бассейны промышленных стоков), которые могут являться источниками дополнительного питания. Все это обычно приводит к резким нарушениям гидродинамического режима, к развитию неста­ционарных процессов фильтрации на площадях, измеряемых подчас сотнями, а то и тысячами квадратных километров. Характерно, что из-за больших (сотни метров) понижений напоров на контурах карь­еров часто отмечается интенсивное истощение водоносных структур — постепенное сокращение их обводненной мощности или (при на­клонном водоупоре) площади. Это обычно делает фильтрационный процесс сильно нелинейным (см. раздел 2.3). Поэтому при прогнозе водопритоков к открытым горным выработкам должны быть тща­тельно учтены не только природные, но и технологические факторы, в частности:

|Т) изменения условий питания и разгрузки водоносных гори­зонтов, связанные с проходкой горных и дренажных выработок и созданием сопутствующих гидротехнических сооружений;

[~2~| технология ведения горных и гидротехнических работ, в том числе порядок вскрытия водоносных горизонтов, изменение по­ложения контура горных работ в плане, режим строительства и экс­плуатации гидротехнических сооружений, распространение и ха­рактер техногенных отложений в пределах бассейнов промышлен­ных стоков.

Если основной объем информации о природных факторах, опре­деляющих притоки в горные выработки, может быть получен уже на стадии гидрогеологической разведки, то многие из упомянутых из­менений в условиях питания и разгрузки, обусловленных техноген­ными факторами, оцениваются на этой стадии лишь весьма прибли­женно (на основе аналогии с подобными объектами). Между тем именно этими изменениями определяются граничные условия филь­трации, и поэтому они обязательно должны изучаться дополнитель­но в период проходки открытой горной выработки - путем постановки и интерпретации режимных наблюдений на базе решения обратных задач (см. раздел 7.2) с последующей корректировкой первоначаль­ных прогнозных оценок.

Прогнозируемые величины водопритоков оцениваются с пози­ций их влияния на условия эксплуатации горнотранспортного обору­дования и на устойчивость откосов карьера (см. раздел 8.1). Если водопритоки превышают допустимые значения, то необходимы дре­нажные мероприятия, обеспечивающие проходку и устойчивость бортов горной выработки (см. раздел 8.2).

2. Схематизация условий фильтрации

Прогнозу водопритоков предшествует обоснование исходной расчетной гидродинамической схемы, охарактеризованной количе­ственно фильтрационными параметрами водоносных горизонтов, ус­ловиями на их внешних и внутренних границах, интенсивностью инфильтрационного питания и параметрами перетекания, а также параметрами горных работ. Непосредственный расчет водопритоков к горной выработке производится либо по аналитическим зависимо­стям — для сравнительно простых (типовых) расчетных схем, либо с привлечением математического моделирования — для слож­ных схем. 0 этоц связи полезно указать следующие признаки типо­вых схем, которые и предполагались нами в предшествующих главах при выводе аналитических зависимостей:

|~Г| простейшая конфигурация области фильтрации в плане (как правило, это схемы неограниченного и полуограниченного пла­стов или пласт-полоса между двумя параллельными границами);

2 однородность и изотропность водоносной толщи или, в неко­

торых частных вариантах, ее упорядоченное (слоистое) строение;

[З] отсутствие дополнительного (по сравнению с естествен- нымУпитания рассматриваемого водоносного горизонта по площади, что позволяет не учитывать площадное питание в явном виде (см. раздел 3.3);

|~4~] совершенство гидродинамических границ области фильт­рации;

[~5] простейшие типовые условия на этих границах (обычно - постоянные условия первого или второго родов);

0 горизонтальное залегание водоупоров, подстилающих без­напорные потоки (в противном случае требуются узко специальные аналитические решения — см. раздел 3.1.7);

0 линейность процессов фильтрации.

Переход от реальных гидрогеологических условий к типовой или сложной расчетной схеме (геофильтрационная схематизация) явля­ется наиболее важным этапом, от которого во многом зависит каче­ство всех последующих прогнозных оценок. Схематизацию целесо­образно проводить по отдельным аспектам расчетной схемы, что дает возможность использовать определенные критерии, контролирую­щие правомерность замены сложной схемы более простой (в частно­сти, допустимость перехода к типовым расчетным условиям). Оста­новимся на основных элементах такой схематизации.

[Т] Фильтрация к открытым горным выработкам, пройденным в удалении от границ обеспеченного питания, обычно является резко нестационарным процессом, однако в области, прилегающей к выра­ботке, реальное нестационарное движение может быть сведено к квазистационарной расчетной схеме. При оценке притока к одиноч-

Мой выработке со стабильными условиями на ее контуре эта цель достигается введением расчетного радиуса зоны квазистационарного режима, который для каждого момента определяется формулой

29. . При наличии границы обеспеченного питания, удаленной от центра горной выработки на расстояние R*, водоприток к выработке с приведенным радиусом г_с может рассчитываться по формулам ста­ционарной фильтрации по истечении времени t > (г* — г₀)²/п а* (см. формулу 4.38).

[~2~| При прогнозе водопритоков к горной выработке контур последней рассматривается как граница дренажа всех вскрываемых ею водоносных горизонтов; на этой границе задаются условия перво­го рода — напоры здесь отвечают отметке нижнего водоупора водо­носного пласта, вскрытого карьером. Если водоносный горизонт за­легает в подошве горной выработки и отделен от нее слоем слабопро­ницаемых пород, то по площади выработки следует задавать условие третьего рода (см. раздел 2.4), — исходя из предпосылок перетекания (см. раздел 2.3.2); впрочем, его можно также трансформировать в условие первого рода, пользуясь принципом эквивалентных фильт­рационных сопротивлений (см. разделы 3.4 и 3.5).

[~3~] Для аналитических оценок водопритоков чаще всего необ­ходимо привести реальные условия к схеме однородного водоносного горизонта, полностью вскрытого горной выработкой, что допустимо лишь при выполнении определенных требований, уже отраженных в предшествующих главах. Так, при вскрытии слоистых водоносных толщ, характеризующихся малым соотношением проводимостей от­дельных слоев (в пределах порядка), движение в них может рассмат­риваться как плановое (см. раздел 3.1); поэтому переход к схеме однородного пласта возможен путем суммирования проводимостей - при напорном режиме, или введением функции Гиринского — для безнапорной фильтрации в горизонтально залегающих слоях (см. раздел 3.1). При больших соотношениях проводимостей отдельных слоев используются предпосылки перетекания (см. раздел 2.3.2); для двухслойных безнапорных толщ в последнем варианте расчет водо­притоков к горной выработке можно вести исходя из проводимости нижнего (относительно проницаемого) слоя и водоотдачи, соответст­вующей емкостным характеристикам верхнего слоя (см. раздел 2.5). Наконец, профильно-анизотропные пласты сводятся к изотропным простым преобразованиям координат (см. раздел 2.5).

4 Максимальные отклонения структуры потока от одномер­ной (вразрезе) наблюдаются вблизи несовершенных горных вырабо­ток. Схематизация структуры потока в этом случае осуществляется с применением локальных профильных математических моделей (см. разделы 3.4 и 3.5) и сводится к определению дополнительного фильтрационного сопротивления, одновременно учитывающего де­формацию потока вблизи выработки и профильную неоднородность фильтрующей толщи. Для однородных пластов и некоторых типов слоистых толщ получены аналитические выражения для расчета до­полнительных фильтрационных сопротивлений [34 ], которые могут быть учтены при рассмотрении планового потока в целом или выде­ленных лент тока.

Принцип эквивалентных фильтрационных сопротивлений или аналогичный ему принцип виртуальных длин (см. раздел 3.1.6) ис­пользуется и для приведения неоднородных в плане пластов к одно­родным.

2. Прогнозы водопритоков на базе аналитических методов

Если схематизация позволяет привести реальные условия к ти­повой расчетной схеме, то, как уже отмечалось, прогнозные оценки базируются преимущественно на аналитических зависимостях, а мо­делирование играет лишь вспомогательную роль.

При очертаниях внешних границ обеспеченного питания, соот­ветствующих типовым схемам (пласт ограничен прямолинейной гра­ницей, пласт-полоса, круговой пласт), определение водопритоков в стационарном режиме проводится по формуле «большого колодца» (3.50), в которой фигурируют соответствующий приведенный радиус области фильтрации R и приведенный радиус карьера г₀ (см. поясне­ния к формуле (3.50)). Наоборот, при существенно удаленных гра­ницах, пока определяемый согласно формуле (4.38) расчетный ради­ус влияния R(t) < R* (R* — расстояние до ближайшей границы), притоки в карьер можно определять как для «большого колодца» по формуле (4.36). При этом величина г. в упомянутых формулах заме­няется на приведенный радиус выраоотки г₀.

В общем случае, при сложной структуре потока в плане, расчет водопритоков к горной выработке целесообразно вести по выделен­ным фрагментам (лентам тока). Боковыми границами фрагментов являются линии хокд, построенные между внешними контурами пласта и контурами горной выработки. Линии тока можно строить на моделях либо непосредственно, либо графически. В последнем вари­анте кажду линию тока проводят от горной выработки в сторону внешних границ обеспеченного питания ортогонально ко всем лини­ям равных напоров (гидроизогипсам).

Стационарный фильтрационный расход рассчитывают незави­симо по каждой денте — по формулам для одномерного плоскопарал­лельного потока (см. раздел 3.1) — после вычисления расчетной длины плоской ленты шириной В_к (рис. 8.9):

ще п — число отсеков между контуром выработки и внешней

границей - контуром питания;

В — ширина расчетной ленты на контуре горной выработки

(В;/ l_t)_cp—среднее отношение ширины выделенных отсеков лен­ты к их длине.

ЗАДАНИЕ. Обоснуйте формулу (8.14) исходя из идеи эквива­лентности фильтрационных сопротивлений (см. разделы 3.4 и 3.5) начальной ленты тока и

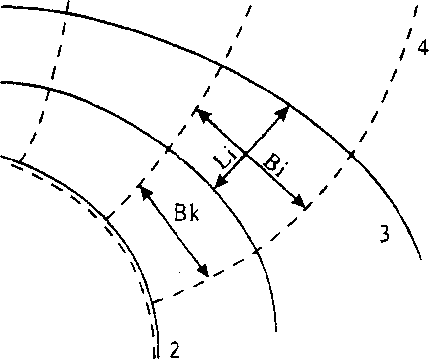
Рис. 8.9. Схема определения расчётной длины ленты тока:

1 - контур питания; 2 - контур горной выработ­ки; 3 - линия разных напоров; 4 - линия тока

расчетной плоской лен­ты.

Расчет по лентам тока можно применять и в условиях неустановив- шейся фильтрации, пользуясь принципом недеформируемости ли­ний тока (см. раздел

3. , согласно которо­му их конфигурация ма­ло меняется во времени и определяется взаимным расположением границ питания и дренажа. Рас­чет в этом случае прово­дится по следующей схе­ме:

[Т] для первых этапов неустановивше- гося режима (внешние границы пласта не влияют на характер потока) приток может быть определен по формуле «большого колодца» при расчете радиуса вли­яния по формуле (4.36);

@ при t > Ft¹/(л а¹) расчет притоков проводится по каждой из лент тока, построенных на модели, или графически с учетом условий на внешних границах пласта. Для этого, согласно изложен­ному в разделе 4.1 (см. также рис. 4.6), в пределах каждой из лент определяют положение условного контура питания на несколько рас­четных моментов времени, затем для участков ленты, ограниченных этим контуром, находят фильтрационные сопротивления (на моде­ли) или их приведенную длину (по формуле (8.14)) и, наконец, проводят расчет фильтрационного расхода на соответствующие мо-

менты времени, — исходя из схемы квазистационарного плоскопа­раллельного потока, по формуле (4.40) или (3.4).

2. Особенности прогноза в условиях сложных расчетных схем

Сложность расчетной схемы при оценке водопритоков к откры­тым выработкам может определяться взаимодействием последних, перемещением фронта горных работ, дополнительным питанием дренируемых горизонтов на локальных участках по площади, нели­нейностью процесса фильтрации. Эти сложности в общем могут быть учтены лишь путем математического моделирования фильтрацион­ного процесса, хотя в частных случаях рассмотрение упомянутых факторов можно вести также в рамках типовых схем, переход к которым осуществляется с привлечением простейших моделей.

Так, исходя из принципа сложения течений (см. раздел 3.3), учет взаимодействия нескольких горных выработок при определе­нии водопритоков к ним в условиях стационарного режима возможен путем приведения каждой выработки к схеме «большого колодца» (соответствующей типовым граничным условиям — см. раздел 8.3.3) с последующим решением системы уравнений вида (3.50), согласно замечаниям в конце раздела 3.3. Определение притоков по отдель­ным участкам контуров выработок приходится вести по выделенным лентам тока или получать цз на плановых моделях непосредственно. Учет взаимодействия выработок в условиях нестационарного режи­ма, как правило, требует применения моделирования в двумерной постановке (см. раздел 4.3): прямое использование принципа сложе­ния течений здесь осложняется из-за задания на контурах выработок граничных условий I рода (см. раздел 3.3).

Перемещение контура горных выработок в плане может суще­ственно определять закономерности нестационарного режима филь­трации. При большой скорости перемещения этот фактор может вызывать рост водопритоков на десятки, а иногда - и на сотни про­центов [9}. Движение контура горных выработок учитывают моде­лированием на сеточных моделях, где отдельные сопротивления от­ключаются в соответствии с перемещением границы дренажа. При­ближенный учет этого фактора возможен с применением моделиро­вания по отдельным лентам тока, опираясь на принцип их недефор- мируемости (см. раздел 8.3.3).

Водоемы и водотоки (естественные и техногенные), подстилае­мые даже слабопроницаемыми отложениями, могут быть источни­ком дополнительного питания водоносных горизонтов, усиленно дренируемых за счет проходки горных выработок . Для учета этого фактора, в общем случае, требуется применение двухмерных сеточ­ных моделей. Впрочем, принцип дополнительных фильтрационных сопротивлений позволяет учесть граничные условия в контурах во­доема или водотока и на простейших моделях из электропроводной бумаги. Аналогичный подход может быть принят при анализе пере­текания по площади дренируемого водоносного горизонта, не вскры­того горной выработкой.

Специального рассмотрения заслуживает прогнозные оценки водопритоков в условиях нелинейных фильтрационных процессов, весьма характерных для осушения многих карьерных полей. В пер­вую очередь, это все задачи, связанные с прогнозом постепенного истощения отдельных участков водоносных комплексов. Такие усло­вия возникают, например, при осушении безнапорных горизонтов дренажными траншеями, отделяющими рассматриваемый участок горизонта от области питания. Процесс нелинейной неустановив- шейся фильтрации описывается при этом уравнением Буссйнёска <2.32), причем линеализацию этого уравнения (см. раздел 2.3.3) можно проводить лишь с большими оговорками, так как трудно по­добрать усредненные значения проводимости или мощности, удов­летворяющие всему расчетному периоду. В этом случае наиболее надежно моделирование по схеме Либмана (см. раздел 4.3.2) или по численным неявным схемам (см. раздел 4.3.3), когда в процессе моделирования изменения проводимости (мощности) безнапорного потока учитывается путем изменения сопротивлений R,_x . между узловыми точками. Так, по схеме Либмана моделирование ведется при стабильной величине «временных» сопротивлений (для случая постоянной водоотдачи осушаемого горизонта), а пересчет сопротив­лений R_x и R производят от шага к шагу по формулам, обобщающим приведенные ранее зависимости (3.77) и (3.78):

А*;

^ ₌ {

^Х* ₍₈₁₅₎

R - ^АУ*

^П к^х^аф (8.16)

ще k_i — коэффициент фильтрации в /-ой точке;

h_i —средняя глубина потока между /-ой точкой и соседними с нею в расчетный момент времени.

Подбор сопротивлений R_x и R на каждом шаге по времени осу­ществляется до тех пор, пока потенциалы в узловых точках не будут соответствовать значениям мощности потока

Приведем более сложный пример определения водопритоков, формирующихся за счет сработки гравитационных запасов подзем­ных вод в планово-ограниченных безнапорных пластах с наклонным водоупором. Вообще говоря, решение задач такого типа должно про­водиться с применением двумерных сеточных моделей: сведение к одномерным задачам с помощью принципа недеформируемых лент тока может иметь здесь лишь ограниченное применение, поскольку в подобных условиях положение линии тока обычно сильно меняется во времени. Однако для простоты мы ограничимся рассмотрением одномерного варианта задачи о вскрытии и постепенном истощении безнапорного пласта с наклонным водоупором, когда необходимо учитывать сразу два фактора нелинейности — изменение мощно­сти пласта и перемещение его контура обводненности в плане (рис. 8.10). Моделирование процесса сработки гравитационных запасов было проведено [9 ] по схеме Либмана с изменением сопротивле­ний R_xi пропорционально глубине потока А_£- от шага к шагу во времени (см. формулу (8.15)). Учет движения границы обводнен­ности осуществлялся изменением пограничных сопротивлений - «временного» R_fr и пространственого к_хг — пропорционально из­менению длины пограничного блока Ах_г. Для этого использовались общие расчетные зависимости: (4.70) и (4.71) при (О = 1 *Адс_г и (8.15)

при Ay_i = 1, Ах; = Ах_г и Щ^р ~h^cp (h^cp— средняя мощность по­тока в пограничном блоке); по мере движения контура обвод­ненности граничные сопротивления постепенно отключались (На рис. 8.10 граничному блоку на текущий момент t отвечает точка 7). По результатам моделирования построены графики в базразмерных координатах, позволяющие проводить оценку из­менения напоров потока и перемещения его внешней граниЦ1ы (см. рис. 8.10).

Из последнего примера видно, что моделирование позволяет не только решить конкретные сложные задачи фильтрации, но и найти для них обобщенные оценки, аналогичные получаемым в рамках аналитических решений.