3. Плановая фильтрация в безнапорном пласте

Особенность этого случая заключается в том, что при снижении депрессионной кривой мощность пласта h из-

меняется, и в расчетный элемент пласта (рис. 2.8) посту­пают дополнительные объемы воды, обусловленные гра­витационной водоотдачей. Если скорость снижения де-

прессионной кривой равна ^то объем дополнительного

О Г

питания на единицу площади пласта в единицу времени равен:

(2.29)

где fx — коэффициент гравитационной водоотдачи.

Соответственно вместо дифференциального уравне­ния фильтрации (2.20) получаем

п —

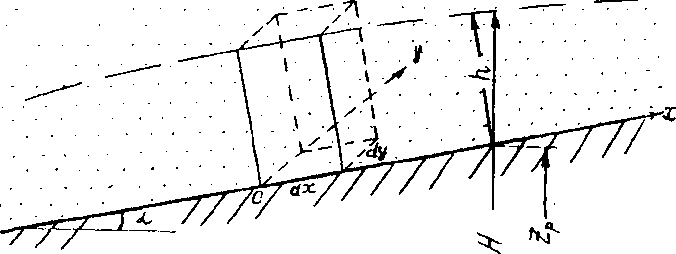
Рис. 2.8. Схема к выводу уравнения плановой фильтрации в безна­порном пласте

Кроме того, в базнапорный пласт сверху поступает вода за счет инфильтрации, удельную величину которой (в единицу времени на единицу площади) обозначим че­резе. Тогда уравнению неразрывности вида (2.5) отвечает уравнение

d и дН\ , d // и & Н\ *дН dh

J_x b^hT_x) ⁺Fv [^ky^hTу) ^{+ £=}" T, ^+fllT,’

(2.31)

где — упругая водоотдача безнапорного пласта.

Так как Я = Zp + h /cos «, или при малых углах «,

характерных для условий безнапорной фильтрации,

д Я д h * *_/

а также ввиду того, что обычно fi » ц (см.

Раздел 1.4), выражением р

можно пренебречь.

а_я 1

dt

Рассматривая далее случай горизонтального водоупо- ра, будем отсчитывать от него значения напоров; тогда Я = h, и уравнение (2.31) примет вид (уравнение Буссине- ска)

Э ■ /, , dh\ д л г. dh\ dh

dx (^kxh dx) dy { y dy) ^ dt ■ (2.32)

Искомой здесь является функция h(x, у, z, t), так что в левой части уравнения коэффициенты при производ­ных зависят от искомой функции, т.е. они заранее неиз­вестны (чего, кстати, не было в уравнениях напорной фильтрации, где мощность пласта задана и не зависит от снижения напоров). Уравнения такого типа называются нелинейными; они существенно сложнее для аналитиче­ского и модельного исследования и поэтому на практике уравнение Буссинеска часто заменяют приближенным линейным уравнением. Для этого делается допущение, что проводимость к h - Т с понижением напора меняется пренебрежимо мало и может быть заменена некоторой средней величиной Т_ср = (к h)_cp, не зависящей от h (лине­аризация по Буссинеску); такой подход вполне правоме­рен, в частности, для типичной схемы двухслойного пла­ста (см. раздел 2.5.2).

ЗАМЕЧАНИЕ. Линеаризацию по Буссинеску можно применить и к более общему случаю безнапорной филь­трации при наклонном водоупоре, тогда уравнение (2.31)

дает:

JL {_T Мл ₊J_ (т M\₊c_=mM

dx dx) ⁺dy {*<** dy) ^+e P dt' (2.33)

что при e = О — формально идентично уравнению на­порной фильтрации (2.22).

Вторая возможность заключается в представлении

и .dh ,

правой части уравнения в виде h -^7, где п_ср — неко-

^Пср "^г

торая усредненная в пространстве и во времени мощность потока; тогда, введя новую функцию и = h /2, мы придем к линейному уравнению относительно и (линеаризация по Багрову-Веригину):

d /, d и\ . а /. а и\ и а и

dx ( х dx) dy ( з- dy) Kpdt' (2.33a)

На практике обычно исполльзуется линеаризация по Буссинеску, которая, как мы покажем позднее, дает хо­рошие результаты для широкого круга задач (см. раздел 2.5).

Для однородных и изотропных в плане пластов лине­аризованное уравнение Буссинеска может быть переписа­но в виде:

V²h+^-=-~,

Т_ср a dt' (2.34)

где

^й=7г* (2.35)

L

д

При линеаризации по второму способу

у2 1 д_и

^и к а dt' (2.36)

где

k-h

^a==-fi^C£-' (2.37)

Итак, в результате линеаризации уравнение безна­порной фильтрации становится формально идентичным

уравнению (2.22а) для напорной фильтрации . В связи с этим параметр а, по аналогии с коэффициентом пьезоп­роводности а¹, получил название коэффициента уров- непроводности; он отражает скорость распространения возмущений в безнапорных пластах. Так как обычно fi »fi, то из сравнения формул (2.35) и (2.23) следует, что в безнапорных пластах возмущения распространяют­ся существенно медленнее, чем в напорных системах (при одинаковых проводимостях примерно в Vfi/ц раз).

Полная математическая эквивалентность конечных уравнений напорного и безнапорного (при горизонталь­ном водоупоре и при отсутствии инфильтрации) движе­ния позволяет нам в дальнейшем приводить выводы и

обсуждения, главным образом, на примере решений для напорного режима. Соответствующие решения для безна­порной фильтрации можно получить, как это следует из приведенных уравнений, путем формальной замены

Н -*h (2.38)

для линеаризации по Буссинеску и бой задачи динамики подземных вод наряду с уравнения­ми, описывающими изучаемый процесс, необходимо за­ранее знать значения искомой функции или ее производ­ных на границах и в начальный момент времени — крае­вые условия для исследуемого дифференциального урав­нения . Благодаря наличию заданных краевых условий соблюдается требование однозначности решения: из множества решений дифференциального уравнения вы­бирается единственное, отвечающее исследуемой крае­вой задаче. Так как в наших задачах искомой функцией является напор Я, то краевые условия записываются для функции Я или ее производных.

Краевые условия задаются для конкретной обла­сти фильтрации — участка земной коры, приуроченного к водоносному горизонту (комплексу) и оконтуренного некоторыми гидродинамическими границами, причем применительно к данной задаче этот участок рассматри­вается как единая, гидравлически связанная система. Кра­евые условия делятся на начальные и граничные.

Начальные условия отвечают исходным напорам в пределах области фильтрации, т.е. напорам на начальный момент времени протекания изучаемого процесса. На­чальные условия должны быть заданы (обычно по резуль­татам измерения напоров в наблюдательных скважинах и их интерполяции) во всех точках области фильтрации в виде известной функции координат:

Я (х, у, Z, 0 |_{r =0} SЯ (х, у, 2, 0) =/_м (х, у, 2). ₍2 39)

Понятно, что начальные условия необходимы лишь при исследовании нестационарных процессов.

Граничныеусловия задаются для всех граничных то­чек области фильтрации (х_г, у_г, z_e) на весь период, рас­сматриваемый при решении данной задачи (основу для этого дают геологоструктурные представления, данные об орогидрографии, результаты опытно-фильтрационных работ и режимных гидрогеологических наблюдений). Как уже отмечено, речь здесь идет о гидродинамических гра­ницах, т.е. о некото­рых, вообще говоря, условных поверхно­стях, где фиксируют­ся те или иные иско­мые характеристики фильтрационного по­тока: скорости, напо­ры или связи между ними. Для того, чтобы лучше уяснить это не­сколько формализо­ванное определение, обратимся к приме­рам.

ТТТТ77~ГТ7ТТТ

ТТТТГ7/ Г/ТТГ

S'

На рис. 2.9,а пока­зана угленосная муль­да, перекрытая водо­упорными покровны- -Рис. 2.9. Схемы закрытого водоносно-

хлы n-rnn,vswuaxMiA- иг» го пласта (а) и безнапорного пласта с ми отложениями, во- _{границей} обеспеченного питания (б)

доносныи пласт углей

и закрытая граница является линий тока. Отметим, что в этом примере гидродинамические границы области филь­трации совпадают с геологическими границами пласта.

На рис. 2.9,6 показан двухслойный безнапорный пласт вблизи реки. При работе инфильтрационного водозабора (речная вода просачивается через пески) его расходы

^/дН} д п

(2.40)

=0,

ограничен водоупорными аргиллитами. При расчете дре­нажных скважин, пройденных на угольный пласт, обла­стью фильтрации является весь этот пласт, гидродинами­ческими границами области фильтрации служат его не­проницаемые контакты с водоупорными породами, . Гра­ницы такого рода мы, кстати, будем называть закрыты­ми, на них фиксируется нулевое значение скорости филь­трации v_n по направлению, перпендикулярному к грани­це; следовательно, согласно закону Дарси

обычно пренебрежимо малы в сравнении с расходами реки. Поэтому можно полагать, что уровни воды в реке и, следовательно, напоры на контуре ее дна практически не зависят от рассчитываемого инженерного сооружения (водозабора) и могут задаваться заранее — исходя из наблюдаемого или расчетного гидрологического режима:

^Нг=/(^хг.Уг.²г, О- (2.41)

Границу такого вида мы будем называть границей обеспеченного питания (здесь — контур дна реки) . За­метим, что водоносный пласт распространяется и за эту границу, так что в данном примере область фильтрации не совпадает с (геологической) областью распространения водоносного пласта; так, для расчета водозабора, распо­ложенного справа от реки, нет необходимости рассматри­вать картину фильтрации слева от нее; влияние водозабо­ра распространится лишь до реки, а уровень подземных вод за рекой не будет зависеть от его работы.

Далее справа на рис. 2.9,6 никаких возможных границ не указано. Это означает, что водоносный пласт распро­страняется здесь «очень далеко», точнее, что за период работы водозабора его влияние не распространится до правой границы пласта. В этом смысле мы здесь имеет дело с полуограниченной (в плане) областью фильтра­ции (говоря формально-математическим языком, правая граница удалена в бесконечность).

Наконец, продолжая обсуждение этого примера, за­метим, что нижняя граница области фильтрации (водо­упорная почва пласта) является здесь закрытой, а верхней границей служит депрессионная поверхность, вдоль кото­рой имеет место свободная инфильтрация с интенсивно­стью е на единицу площади пласта. Следовательно, здесь задано условие

ЗАДАЧА. Показать (рассуждением от противного), что При от­сутствии инфильтрации депрессионная кривая стационарного пото­ка является линией тока.

Кроме того, на свободной поверхности избыточное гидростатическое давление равно нулю и напор равен геометрической высоте, т.е. здесь задано дополнительное условие

(2.43)

Н ~ z.

На рис. 2.10,а показана совершенная водопонижаю­щая скважина с радиусом г_с в неограниченном (в плане) напорном пласте. Однако в этом примере у области филь­трации имеется внутренняя граница — контур скважины радиуса г_с. Если скважина откачивает воду с постоянным расходом Q_c, то, согласно закону Дарси

^удН}

Зг

‘дФ

3 п

2 ж^щТ'Г_

О =ко)'1, — 2 К'Г'к'Ш

г ?. ?. г

где ш_{ и 1_г

(2.44)

соответственно площадь граничного сечения и градиент на границе;

п

нормаль к границе, совпадающая с направле­нием радиуса г.

3 п

2п-г-Т'

<3 Я^Х

Следовательно, на рассматриваемой внутренней гра­нице задана нормальная производная функции Н:

(2.45)

В этом примере границей области фильтрации являет­ся, таким образом, контур инженерного сооружения.

На рис. 2.10,6 показан контакт аллювиальных песков (1) в долине реки с известняками (2). Область фильтра­ции является полу ограниченной (внешней границей слева служит река), но имеет внутреннюю границу — контакт водоносных пород с различными фильтрационными свой­ствами (граница раздела). Из условия неразрывности потока через эту границу получаем равенство скоростей фильтрации v_nl и v_n2, нормальных ей, или, по закону Дарси

^/зн}

д П

^/вн} д п

а

_П-_ГГГГГ7-_ГГГ7^_Т^

г**

5

ушшр I ^ ri'-IU^y II

Рис. 2.10. Схемы совершенной скважины в неограниченном пласте (а) и области фильтрации, содержащей границу раздела — кон­такт водоносных пород с различными фильтрационными свойст­вами (б)

xpiE^iiEr:

(2.46а)

Кроме того,

Рис. 2.11. Преломление линий тока на границе двух зон с различной проницаемостью

(индексы 1 и 2 относятся к соответственным точкам по разные стороны от границы).

ЗАДАЧА. Доказать аналогично известному закону преломления в оптике, что на контакте двух зон линии тока стационарного потока претерпевают излом (рис. 2.11) — в соответствии с формулой

tgO1 _k^

~ *2 ’ (2.47)

где 0J и $2— углы отклонения от нормали.

ЗАДАЧА. На рис. 2.12 показан карьер 2 вблизи реки 1, для защиты которого пройден ряд дренажных скважин 4. Нормально к реке проходят два непроницаемых сброса 3. Какова область фильт­рации: а) при прогнозах притоков в карьер, полностью вскрывающий водоносный пласт; б) при прогнозах работы дренажного ряда?

Приведенных примеров, очевидно, достаточно, чтобы мы могли далее оперировать понятиями область фильт­рации и гидродинамическая граница (далее —- просто граница). Одновременно мы познакомились с некоторы­ми видами граничных условий. Для более систематиче­ского использования граничных условий, при дальней­шем изложении введем следующую их классификацию, принятую в математической физике.

[Т] Граничные условия I рода — на границе задано значение напора (см. формулу (2.41)). Такие условия, в частности, характерны для (рис. 2.13,а-г) а — рек, водо­емов и других границ обеспеченного питания; б — естест­венных контуров стока, приуроченных к нижнему водо- vnopy водоносного пласта или определяемых уровнем в

водоеме; в — горных выработок, отметка выхода воды в которые также определяется отметкой нижнего водоупо- ра или отметкой дна выработки, или уровнем воды в затопленной выработке; г — скважин, работающих с за­данным на них напором (самоизливающих, поглощаю­щих и т.д.). Частным случаем границы I рода является граница с постоянным Напором.

Рис. 2.12. Схема области фильтрации

~2] Граничные условия II рода — на границе задано значение расхода или нормальной составляющей скоро­сти, точнее — нормальной производной . Такие

о п

* \ /^г условия наиболее характерны для закрытых границ (см.

формулу (2.40)) и для скважин, работающих с заданным

расходом, равным номинальной подаче установленного в

них насоса (см. формулу (2.45)); при этом расход Q_c

может быть и переменным во времени.

[71 Граничные условия III рода — на границе задана прямо-пропорциональная связь между расходом и напо­ром, точнее — между искомой функцией и ее нормальной производной:

'он'

д п

= а-Н_г+р,

где а и/? заданные постоянные.

-_Г^_Г-_Т~₇~уГ-.._/..у_{Г 7}«_Г-_?.^_Г

а

7"~7 " / ' *7—т—v—г

заранее не известны, то

-т~

"7““Г“Т“"Г~7—-} 7~Т

Рис. 2.13. Варианты границ пласта с условиями Iрода гг U

Так как значения Н_г и

д п

Н.-Н,

условие (2.48) является нелинейным (см. раздел 2,3). Условия третьего рода наиболее характерны для контак­тов водоносного пласта с относительным водоупором, че­рез который идет перетекание (см. рис. 2.7) или переток воды из открытого водоема (рис. 2.14), когда роль отно­сительного водоупора играет тонкий слой (мощностью т_п) илистых отложений с коэффициентом фильтрации к_п. Скорость перетекания, равная, по условию неразрывно­сти, нормальной компоненте скорости фильтрации в во­доносном пласте — на его границе с относительным воло- упором, — выражается в виде

(2.49)

где Н„ — заданный напор в водоеме,

Н_г — неизвестный напор в пласте, непосредственно под слабопроницаемым слоем).

Рис. 2.14. Схема разгрузки подземных вод в водоем с граничным условием III рода

Откуда получаем условие (2.48) при

к'т„ к-т„

К ft

Заметим, что граница водоема здесь не считается кон­туром обеспеченного питания и является, таким образом, примером границы, несовершенной не только по степени вскрытия, но и по характеру вскрытия: связь поверхно­стных вод с подземными вдоль границы не непосредствен­ная, не свободная, а усложненная наличием слабопрони­цаемых (экранирующих) отложений.

ЗАДАЧА. Покажите, с учетом выражения (2.26) для модуля питания на верхней границе нижнего водоносного пласта (см. рис.

К ~К'^Н

поп 1

московский 2

ДИНАМИКА ПОДЗЕМНЫХ 4

вод 4

О, = о_с-G„ =(Д„ — Д₀)(1 -n)-z=y,-z, 44

_/=^^а«.._с._й, ш 85

шшшш 145

^(4^)⁺f,(^r'5)^+£=°- 176

¹±шл ' 280

ДШш§ 443

[Т] Граничными условиями IV рода называют сово­купность условий (2.46) и (2.46а) на поверхности разде­ла.

В заключение напомним, что наряду с подобием диф­ференциальных уравнений (см. раздел 2.2.4) подобие краевых условий является необходимым признаком для математической аналогии, лежащей в основе моделирова­

ния геофильтрационных процессов. Отметим в этой свя­зи, что принципы обеспечения такого подобия для выде­ленных типов граничных условий на электрических мо­делях в большинстве своем достаточно очевидны из при­нятой аналогии (см. раздел 1.7). Так, условие первого рода моделируется заданным потенциалом на границе, условие второго рода — током заданной силы, подавае­мым на соответствующие участки границы , условия чет­вертого рода выполняются автоматически. Несколько сложнее обстоит дело с нелинейными условиями третьего рода, которые, согласно формуле (2.48), требуют подбора заданного соотношения между потенциалом и силой тока. Наконец, при моделировании профильных безнапорных потоков также приходится сталкиваться с нелинейностью на границе: само положение верхней границы потока - депрессионной кривой — оказывается зависящим от ис­комой функции; поэтому границу модели подбирают в процессе моделирования согласно условию (2.43). На­пример, на профильной бумажной модели бумагу посте­пенно подрезают до тех пор, пока во всех точках линий обреза не окажется выполненным условие (2.43).