2. Макродисперсия в гетерогенных системах упорядоченного строения

Этот вопрос проще всего рассмотреть на примере двух слоев с резко различными значениями проницаемости (рис. 6.12). В зависимости от масштаба и времени мигра­ции для такой системы возможны две предельные расчет­ные схемы.

Для начальных моментов расчетная схема предпола­гает, что слабопроницаемый слой обладает неограничен­ной емкостью, т.е. влияние молекулярно-диффузионно­го переноса в этом слое не достигает его внешней границы.

Л?

О

I • •

.¹4 •'

н,-

■ -£>__*■

тп—г"- X

• I '. '. '

п.т

м

У

у / / / ТТТТТ’Т”Л”'у--'пг 7~~Т~Т~Т~~ М'

.В

Рис. 6. /2. Схема миграции подземных вод в двуслойном пласте: j - хороиюпроницаемый слой; 2 - слабопроницаемый слой; направления потоков: 3 - конвективного; 4 - диффузионного; ММ и NN - границы расчетного элемента, непроницаемые для воды и вещества; 5 - положение концетрационного фронта на различные моменты времени t

Критерии допустимости такого предположения нетрудно пол­учить, решая уравнение молекулярно-диффузионного переноса для концентрации с в слабопроницаемом слое:

п,

м

(6.34)

dcp (х, z, t) д²с₀(х, z, t)

dt

которое получается аналогично (6.21) при v *0 (D= Dj. Координата z отсчитывается от контакта слоев. Уравнение (6.34) идентично уравнению нестационарной фильтрации (4.1). Поэтому, если счи­тать, что вблизи точки х * 0 в водоносном слое поддерживается неизменная концентрация с = 1, то, аналогично разд. 4.1, получаем решение фундаментальной задачи для уравнения (6.34)

с₀ (х, z, t) = erfc

L2V^7n₀)rJ’ <«-зя

справедливое при малых х, т.е. вблизи исходного сечения солевого потока. Далее, по аналогии с формулой (4.18), где вместо коэффици­ента пьезопроводности а должно фигурировать отношение D_M/n_Q, получаем, что отток вещества на границе контролируется расчетной зоной влияния:

Ясно, что внешняя граница слабопроницаемого слоя не влияет на процессы переноса в фильтрующем слое, пока zjt) ^ m_o.

Отсюда получаем временной критерий справедливо­сти расчетной схемы неограниченной емкости:

(6.37)

Считая, что для глинистых разделяющих слоев D_M примерно равен (2¹3) 10'⁵ м²/сут, а п₀~ 0,4, получаем ориентировочный критерий:

(6.38)

t_H < 10⁴ ml

(время — в сутках, мощность — в метрах), т.е. схема неограниченной емкости может применяться очень широ­ко даже для сравнительно маломощных (метровых) раз­деляющих слоев .

При пренебрежении микродисперсией в фильтрую­щем слое (см. рис. 6.2) решение поставленной фундамен­тальной задачи для схемы неограниченной емкости дается формулой [37]:

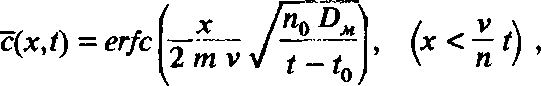
(6.39)

слое;

где v — скорость фильтрации в хорошо проницаемом

п — его активная пористость; t_Q - хп / V.

Формула (6.39) известна как решение Ловерье; при двустороннем оттоке (вверх и вниз) в ней следует опу­стить коэффициент 2.

Для вывода формулы (6.39) вернемся сначала к уравнению

19. для водоносного пласта, считая, что дисперсией в пределах последнего, т.е. членом Dm(dc/dx), можно пренебречь. Учтем,

однако, что через кровлю пласта в выделенном элементе длиной dx идет отток вещества с интенсивностью, равной (см. формулу (6.13)):

ttt

l₌₀.

dc ,

^mnTi 7Гх

Тогда, аналогично уравнению (6.21), получаем:

^дс = п I

■^и - I - — Л •

Применяя к этому уравнению преобразование Лапласа-Карсона

(4.42), получаем

О

тис, д с „ д с,

——-Tfflv3— = D_u - 1 __л,

t дх ^м dz \z— O’

где с — изображение функции с.

Уравнение (6.34) для слабопроницаемого слоя принимает в изо­бражениях вид

*•*' т 2 '

^С0 — п ^П0* ^Dm - 2 ' ^lp dz

= с _ =0 ,

I z — m ’

Решая его при граничных условиях ^с0 |_z =0 ^с ’ ^с0 |_z-> оо получаем [16]:

с₀ = с ехр

Отсюда

£51

dz z

пп , /£м%\

Ч J ч)

У равнение в изображениях для водоносного слоя принимает вид

(тп

~ I dc _Л

с + т v~г~ =0. dx

oq — Cq легко находим, разделяя переменные:

L\

vt„

п

_ -р — * Р } _

с = с₀ exp

По таблице изображений [16] получаем оригинал — решение (6.39).

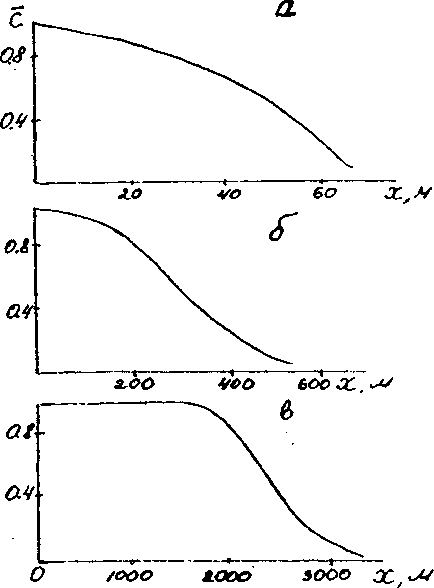
ЗАДАЧА. Проведите расчет по формуле (6.39) для следующих характер­ных значений параметров (см. рис. 6.12): т=0,1 м; m = 0,2 м; п - п_о - 0,5; D * 5 • 10 м /сут; v=0,5 м/ сут. Постройте выходные кри­вые: с(0 для точки х - 40 м и с(х) для времени t- 70 сут (убедитесь предваритель­но, что выбранное время удовлетворяет критерию (6.37)).

Характерный гра­фик изменения кон­центрации в простран­стве приведен на рис.

13. а. Из него, в част­ности, видно, что раз­меры переходной зо­ны, обусловленной от­током вещества в сла­бопроницаемый слой, Рис. 6.13. Характерные графики изме- могут быть СОПОСтави- нения концентрации по направлению мы с общей длиной пе- переноса в гетерогенных комплексах _ПР„_ЛГЯ _ ~ пягграикр (положения а, б ив отвечают увеличе- ^ ’ ; рассеяние

нию времени переноса) вещества (макродис-

персия) идет намного

При этом используется правило Lj [/{л; t — CL)} — е~^*Р'F(x,t) meLy — обозначение преобразования Лапласа-Карсона (см. раздел 4.2).

интенсивнее, чем в случае однородного пласта (см. раздел 6.3).

Вторая предельная схема исходит из предположения, что при длительном протекании процесса в рассматри­ваемой двухслойной системе (см. рис. 6.12) диффундиру­ющий раствор заполняет слабопроницаемый слой на всю его мощность. Будем называть ее предельной схе­мой макродисперсии. Скорость движения фронта рас­твора v¹ определяется при этом так же, как и скорость поршневого вытеснения:

^vn * »

* v

~п ' (6.40)

где величина п характеризует суммарную емкость систе­мы (приведенную к мощности т):

* — _1 ^то ^п ~^п "о т • (6.41)

Можно показать [34], что для описания процесса пе­реноса в основном пласте справедливо выражение, анало­гичное решению (6.27), полученному в рамках схемы микродисперсии (см. раздел 6.3). Однако диалог парамет­ра D— коэффициент макродисперсии D — пропорцио­нален здесь квадрату скорости фильтрации, личиваются и размеры переходной зоны. Следовательно, при макродисперсии роль эффектов рассеивания веще­ства проявляется гораздо сильнее, чем в условиях рас­четной схемы микродисперсии, так что ими часто нельзя пренебрегать даже в пористых породах.

Критериями применимости предельной схемы макро- дисперсии могут служить условия [21]:

X - — /— > 10 ; х<Ц.

^п т₀ (т₀ п₀ + т п) _п* (6.44)

Первое условие исходит из требования достаточно полного насыщения слабопроницаемого слоя — для то­чек, удовлетворяющих второму условию. Последнее, в свою очередь, означает, что рассмотренное решение до­статочно хорошо описывает распределение концентрации лишь на задней части фронта (с > 0,5), так как в его передней части параллельный перенос никогда не дости­гается: значительный объем слабопроницаемого слоя всегда остается здесь недонасыщенным по отношению к концентрации в основном слое.

Характерный график пространственного распределе­ния концентрации для больших отрезков времени (отве­чающих первому из критериев (6.44)) приведен на рис.

13. в. Сравнивая его с рис. 6.13,а, нетрудно убедиться, что по мере миграции в гетерогенной среде форма графи­ков концентрации качественно изменяется — в отличие от миграции в гомогенной среде (см. рис. 6.10,6).

Мы рассмотрели водоносную систему, состоящую из слоев пород с резко различающимися коэффициентами фильтрации, благодаря чему мы пренебрегли горизон­тальной конвекцией в пределах слабопроницаемого слоя. Для случая переслаивающихся пород с достаточно близ­кими проницаемостями такой подход, конечно, недопу­стим. Правда, можно вспомнить, что в теории плановой фильтрации привычно вводить для подобных систем ус­редненную проводимость пласта (см. раздел 2.5). Однако в теории массопереноса всякие усреднения характери­стик по мощности пласта следует проводить с боль­шой осторожностью, прежде всего потому, что флукту­ации поля скоростей по мощности подземного потока ведут к дополнительному «размазыванию» концентраци­онного фронта — аналогично гидродисперсии. Как и в предыдущих случаях, такую зависимость эффектов рас­сеивания вещества от колебаний гидравлической прово­димости водоносного пласта можно связать с понятием макродисперсии. Характерная длина, определяющая мак­родисперсию (по аналогии с параметром микродисперсии <5j), имеет в этом случае порядок величин мощностей

водоносных слоев.

Далее, необходимо учитывать и поперечное гидродис­персионное перемешивание между отдельными слоями, которое играет ту же роль, что молекулярная диффузия в расчетной схеме микродисперсии: оно является факто­ром, направленным на выравнивание концентраций меж­ду элементами с различной проницаемостью. Проиллю­стрируем особенности проявления макродисперснионных эффектов в слоистых системах с близкими фильтрацион­ными свойствами на примере двухслойного пласта (рис. 6.14). Массоперенос в таком пласте характеризуется дву­мя крайними режимами [21]:

1

начальным, когда поперечная дисперсия практи­чески еще не успевает проявиться и поэтому каждый слой «работает» независимо один от другого, ооеспечивая пе­ремещение вещества с резко различными скоростями (весьма близкими к значениям vjп_х и v₂! п₂);

[ 2 конечным асимптотическим, когда влияние по­перечного обмена захватывает весь пласт, обусловливая выравнивание скорости перемещения фронта по всей мощности пласта. Верхний предел применимости расчет­ной схемы послойного Переноса t_n легче всего опреде­лить, вернувшись к водоносной системе со слабопроница­емым слоем (см. рис. 6.12): потребуем, чтобы время пе­ремещения фронта переноса (с концентрацией с ^ш 0,5), определенное по формуле (6.39), не слишком сильно ot^j личалось от времени t# найденного из схемы поршневогб вытеснения (t_n/t₀ = 1+е, где £ — заданное малое число).

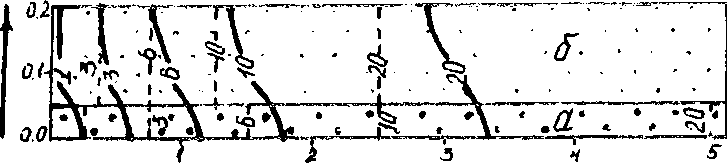
F5=|/ ГП£

ЪиряирмаЧ кмнДхигов^

Рис. б. 74. Характер массопереноса в двуслойном пласте ( по резуль­татам математического моделирования):

а и б - более и менее проницаемые слои соответственно: сплошные изолинии 7—0,5 — с с учетом полперечной дисперсии; пунктирные - при отсутствии взаи­модействия между слоями. Числа на изолиниях - расчетные моменты времени, сут.

ЗАДАЧА. Сделайте это самостоятельно; покажите справедли­вость соотношения:

т\²

(6.45)

(для возможного двустороннего оттока).

Из формулы (6.45) следует, что схема послойного переноса может применяться довольно широко. Напри­мер, для переславивающихся песчано-глинистых пород (D_M » 2,10*⁵ м²/сут; п » п₀ » 0,4) при е * 0,02 получаем t_n » 100 т²(сут), т.е. для метровых песчаных прослоев время t_n измеряется годами.

Заметим вместе с тем, что при близких проницаемо­стях слоев (см. рис. 6.14) формула (6.45) будет давать завышенные значения t_n. Нужно учитывать, что в этом варианте обмену между слоями будет способствовать так­же поперечная гидродисперсия, и тогда в формуле (6.45) коэффициент молекулярной диффузии D_M следует заме­нить коэффициентом поперечной гидродисперсии D', оп­ределяемым по формуле (6.17). Это приведет к тому, что, например, в трещиноватых крупноблочных породах, где параметр д' измеряется метрами - десятками сантиметров, время t_n может уменьшаться — в сравнении с только что приведенными оценками — на несколько порядков.

В таких условиях, как, впрочем, и для тонкого пере- славивания песчано-глинистых пород, относительно быс­тро устанавливается асимптотический режим, форма фронта переноса стабилизируется, и он перемещается со средневзвешенной скоростью

= Zi ^mi ^{+ v}2 ^W2

^v« mj /ij + m₂ n₂ ' (6.46)

ЗАДАЧА. Обоснуйте формулу (6.46), исходя из предположения, что фронт переноса (изолиния относительной концентрации с = 0,5) не меняет своей формы, как это, например, показано на рис. 6.14 для

времени t > 10 сут.

Отметим, наконец, что если в слоистых, достаточно хорошо проницаемых пластах мигрируют минерализо­ванные стоки, плотность которых отличается от пласто­вой воды, то интенсивность межслоевого взаимодействия может определяться преимущественно процессами грави­тационного характера (см. раздел 6.1.2), а поперечное дисперсионное перемешивание имеет тогда подчиненное значение. Чтобы лучше уяснить это положение, верни­тесь еще раз к задаче о плотностной конвекции в разделе

6.1.2.