3. Конвективно-дисперсионный перенос в однородных водоносных пластах

Еще раз напомним, приступая к дальнейшим исследо­ваниям задач переноса, что мы ограничимся рассмотрением жидкостей с постоянной плотностью (и вязкостью). Это позволяет значительно упростить анализ миграционных процессов: «фильтрационная часть» задачи может решаться заранее, отдельно, — независимо от задачи переноса; поэ­тому фильтрационное поле считается нами заданным.

1. Фундаментальное решение

Рассмотрим совместное проявление конвекции и дис­персии в однородном пласте, сложенном гомогенными водоносными породами — пористыми или «чисто» трещи­новатыми (рис. 6.10,а). Фильтрационный поток считаем одномерным (плоскопараллельным) и стационарным. Исходная концентрация вещества повсеместно равна с°. В момент t = 0 концентрация на левой границе Принимает постоянное значение с₀ и соленые воды начинают переме­щаться по пласту в направлении оси х. Поток соли д_с через произвольное сечение пласта обусловлен конвекцией (q'_c ~cq, где с(х, t) — текущее значение концентрации; q — удельный расход фильтрационного потока) и диспер-

д С

сией (q_c" = — D т — согласно закону Фика):

Q_c=Q_c'+Q_c"-cg-Dm^. ₍₆₁₉₎

Составим уравнение неразрывности для элемента dx:

Qc dt ~ [<7_С - ~ ^dx\ dt=Y_t(nmc) dx dt, _{(6 2Q)}

где справа записано приращение количества соли в эле­менте dx [с объемом порового пространства, равным nmdx, причем при наличии сорбции величина п заменяет­ся на п_э согласно (6.11)] за время dt, а слева —разность между количеством соли, поступившей в этот элемент и вытекшей из него за то же время dt. Подставляя сюда выражение (6.19) для q₀ приходим к дифференциальному уравнению конвективно-дисперсионного переноса отно­сительно неизвестной концентрации с(х, 0:

вс , вс ~ д²с п —; + V—- =D

dt дх дх²' (6.21)

CL

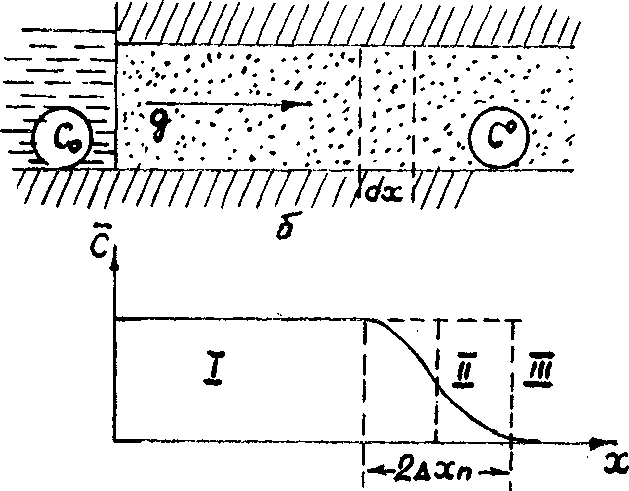
Рис. 6.10. Схема миграции в водоносном пласте (а) и характерный график пространственного изменения концентрации (б)

Начальное и граничные условия имеют вид: с (х,0) = с⁰ (х > 0);

■ c (0,t) = ^co (t > 0);

с (оо,0) = с® (6.22)

Последнее граничное условие физически эквивален­тно условию отсутствия гидродисперсионного переноса в

^оне с постоянной (исходной) концентрацией с⁰

ff(»,0=О

Введем относительную концентрацию

(6.23)

и получим окончательную математическую формулиров­ку фундаментальной задачи миграции:

^со~^с

д²с д х²

дс , дс ⁿ~bt^+VJlc

D

(6.24)

с (х,0) — 0 (х > 0);

с (0,f) = 1 (f > 0);

_с(оо,0)=0. (6.25)

к

Решение этой задачи [37], формально напоминаю­щей фундаментальную задачу фильтрации (см. раздел 4.1), находится операционным методом (см. раздел 4.2):

с - 0,5 {erfс | + {erfс | ^ , (6.26)

1

х > — п

\

где

У X

D

£ = ^х ~ (^v • А = дс -Н Cv t//i) . с.

2 'fD t f n ’ ¹ ~ 2 ЛсГЛНп'

a erfc(z) — уже использованная нами табличная функ­ция (см. раздел 4.1).

При достаточно больших rj вторым членом в правой части (6.26) можно пренебречь, внося при этом погреш- 0 3

ность е = -jj- [34]. Тогда решение принимает вид

с = 0,5 erf с £. (6.27)

Графическое представление решения (6.27) дается на рис. 6.9,6. На графике выделены три зоны: I — зона вытесняющего раствора, III — зона вытесняемого раство-

ра и II — переходная зона , в пределах которой относи­тельная концентрация меняется от значений, близких к 1, до значений, близких к 0. На рисунке пунктиром показан также график изменения концентрации при поршневом вытеснении, когда дисперсия отсутствует (D = 0). Понят­но, что точка х_п, согласно (6.1), отвечает условию

₌ vt

^х* п (6.28)

и, следовательно, в случае, описываемом решением (6.27), с( х_п) =0,5 erf с (0) =0,5, т.е. точка х_п располагается посредине переходной зоны. Физически это вполне по­нятно: на фоне продвижения фронта поршневого вытес­нения, отвечающего конвекции, развивается дисперсия, приводящая к размыванию фронта, симметричному отно­сительно его расчетного положения х_п.

Размер переходной зоны 2 А х_п можно оценить, услов­но считая ее заключенной между значениями с = £ и с = 1 - е, где е — некоторая малая величина. Например, полагая е =8%, получим с =(х + Ах_п) = 0,08, чему, согласно решению (6.27) и таблице функции erf с Z, отве­чает £ ~ 1,0. Отсюда

х + А х„ — (v/n) t

2 'ГЬ х Тп А= 2 yfDlTn , (6.29)

где половина ширины переходной зоны А х_п может быть

названа величиной «обгона». С учетом формулы (6.15), выражение (6.29) можно записать в следующем виде:

Дх„ = 2 = 2 + Л,) *. = 2 'TCDjnjx^

(6.29а)

откуда

А*„ _ 2

^ХП УРё’ (6.30)

* На первых этапах переходная зона несимметрична относительно точки средней концентрации (см. формулу (6.26)), а расчетное положение фронта х„ несколько сдвинуто относительно нее влево.

— безразмерный критериальный параметр Пекле.

Из выражения (6.30) следует, что при больших зна­чениях Ре (порядка тысяч) наличием переходной зоны - в сравнении с общим продвижением фронта х_п — можно пренебречь. Так как

_P/,-^VXn_ ^V*n ₌ *п

^{D D}M^+d 1^V <*i^v (6.31a)

TO

Ax„ 2 ^

-^^тш^т

и ориентировочно можно полагать, что дисперсией допу­стимо пренебречь при

yf3^/x_n<e, (6.32)

где е — некоторое малое число.

Например, полагая е * 1 %, приходим к условию:

д_х < 0,0001 х_п . (6.32а)

Отсюда сразу видно, что в натурных условиях при переносе на расстояния, измеряемые сотнями метров и километрами, дисперсией в однородных песках можно пренебречь , в то время как в трещиноватых породах это обычно недопустимо; нельзя пренебрегать диспер­сией и при проведении экспериментальных работ (когда расстояния переноса не превышают первых метров - де­сятков метров) — в породах любого типа.