6.1.4. Задача об определении скорости фильтрации скважинной резистивиметрией (термометрией)

В качестве простейшей задачи конвективного массопереноса, имеющей, однако, большое практическое значение, рассмотрим за­дачу об определении скорости фильтрации в естественном потоке подземных вод резистивиметрией (или термометрией) наблюдатель­ной скважины. При этом в скважину запускается индикатор — соль (или вода с температурой, отличающейся от пластовой), равномерно распределенный вдоль фильтра длиной I, и радиусом г.. За выносом индикатора, обусловленным подземнымтютоком в области фильтра (рис. 6.5), наблюдают по резистивиметру (измеряющему электро­сопротивление воды, однозначно связанное с концентрацией инди­катора ) или терморезистору (измеряющему температуру воды). Дальнейший вывод проведем для солевого индикатора [34 ]:

Баланс индикатора в скважине за время выражается условием

Q_c (^с ~ ^с°) ^dt ~ ~^Жгф ¹ф ^dc ’

о

где с и с —исходная и текущая концентрации.

Расход воды, протекающей через скважину определяется скоростью фильтрации v и поперечным сечением потока ((О = 2Гф :

Q_c = ² £ ^гф ¹ф ^v »

где £ — коэффициент искажения потока вблизи скважины (см. рис. 6.5), зависящий от состояния фильтра (скин-эффекта, см. раздел 5.4).

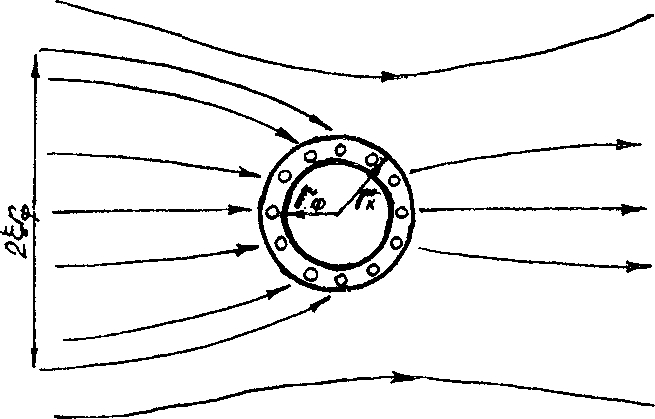
Рис. 6.5. Схема линий тока вблизи наблюдательной скважины

При отсутствии скин-эффекта £ = 2, но в целом эту величину рекомендуется определять по данным опытно-фильтрациОнных оп­робований [21, 34].

Итак, мы приходим к уравнению

dt.

I£v

Если замеренная начальная концентрация индикатора с I ^ — c_Q, то, интегрируя, получаем формулу для определения v.

„ о

_^Пгф_Л ^с0~^с

<6.12)

На графике зависимости lg [(c_Q — с°) / (с —с⁰) ] от времени t опытные точки должны, таким образом, ложиться на прямую линию, по уклону которой и находится неизвестная скорость фильтрации.

Формулу (6.12) можно использовать и по-иному, если опытная скважина находится в области влияния откачки. Тогда, зная по де­биту откачки значение скорости фильтрации v в точке расположения

скважины, можно определить коэффициент искажения потока а по нему — значение скин-эффекта наблюдательной скважины.

2. Диффузионно-дисперсионные процессы

1. Молекулярная диффузия и гидродисперсия

Явления диффузии в свободной жидкости достаточно общеизвестны.

ВОПРОС. Почему брошенный в стакан кристалл медного купо­роса постепенно вызывает окрашивание всей массы воды в стакане?

Аналогично в водонасыщенных горных породах, при наличии градиента концентрации, возникает самопроиз­вольный перенос вещества под действием молекуляр­ных сил. Общий поток вещества Q_D в направлении I

через расчетное сечение ш₁ при этом ориентирован в сто­рону уменьшения концентрации с и определяется зако­ном Фика:

п - _ п —-

^Udm ~ (6.13)

где D_M — коэффициент молекулярной диффузии в пори­стой среде, зависящий от ее структурных особенностей и физических свойств поровых растворов (его характерные значения для песчано-глинистых пород имеют порядок 10' м /сут). Для сорбируемых компонентов величина D_M, соответственно, убывает.

Скорость чисто молекулярного диффузионного пере­носа, как правило, мала, и учитывать ее следует только при малых скоростях фильтрации, в первую очередь - при оценке массопереноса через слабопроницаемые породы - разделяющие слои, экранирующие отложения хранилищ промышленных стоков, пористые блоки трещиноватых пород и т.п. Молекулярная диффузия проявляется при фильтрации воды как фактор рассеяния, действующий между жидкостями с различной концентрацией на фронте вытеснения.

В конечном счете _с

внешним проявлением диффузии во всех случаях

оказывается «размыв» с₀

границы между вытесняе­мой и вытесняющей жид­костями, образование

вблизи фронта вытесне- ^с° \

ния переходной зоны L_n,

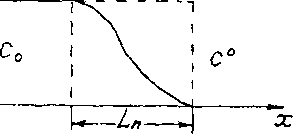
В пределах которой кон- Рис. б-6- Характерный график

центрация вещества изме- ^пР°странственого изменения ш, концентрации при наличии диф-

няется постепенно от С₀ ДО фузии или гидродисперсии с° (рис. 6.6), в отличие от

резкой границы, характерной для чисто конвективного переноса (т.е. для схемы поршневого вытеснения). По такому внешнему проявлению с молекулярной диффу­зией ассоциируется еще один механизм переноса вещест­ва — механическая дисперсия.

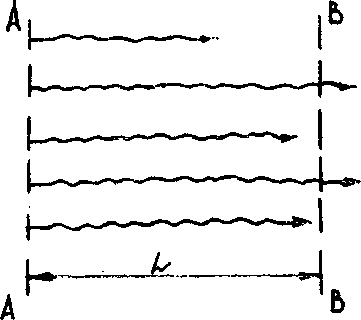
Однако природа этого явления существенно иная: ме­ханическая дисперсия обусловлена неоднородностью по­ля действительных скоростей. Если, например, все окра­шенные частицы воды (рис. 6.7) начинают одновременно двигаться в фильтрационном потоке, имеющем среднюю действительную скорость v_a, от поперечного сечения АЛ в направлении ВВ, то за время t-Llv_d одни из этих частиц пройдут путь существенно больший, чем L, а другие — меньший. В результате вместо резкого контакта окрашен­ной и неокрашенной жидкости, характерного для началь­ного момента (сечение АЛ), вблизи сечения ВВ этот кон­такт окажется размытым — вследствие рассеяния окра­шенных частиц фильтрационным потоком. Согласно экс­периментам, подобное рассеяние, называемое фильтра­ционной диффузией, или механической диспер­сией,также подчиняется закону Фика (6.13), однако при замене коэффициента молекулярной диффузии D_M на другой параметр — коэффициент механической диспер­сии D_&

Как показывают эксперименты, при достаточно боль­ших скоростях фильтрации v в однородных грунтах вели­чина D_d оказывается при­мерно пропорциональной скорости фильтрации v:

^Dd^=di^v> (6.14) где константа <5_Р называе­мая геометрическим пара­метром механической дис­персии, имеет размерность длины и коррелирует с раз­мером элементарных со-

„ _ ^ , ставляющих фильтрующей

Рис. 6.7. СХ6М&движениячастиц плплптт ТТття пиновпиных жидкости в пористой среде породы. ДЛЯ однородных

песков параметр dj имеет

порядок миллиметров, а для трещиноватых пород — по­рядок расстояний между основными водопроводящими трещинами (поэтому нередки случаи, когда <5j измеряется

метрами, а то и десятками метров [21,41]).

В результате при больших скоростях потока величина D_d может на несколько порядков превосходить характер­ные значения коэффициента молекулярной диффузии.

Аналогия в характере проявления молекулярной диф­фузии и механической дисперсии способствовала их объ­единению через суммарный коэффициент:

^{D = D}M⁺⁰d=0_M+d_lV, (6.15)

i -

который далее (для краткости) будет именоваться коэф­фициентом дисперсии.

Соответственно суммарное рассеяние вещества, вы­зываемое гидродисперсией, или просто дисперсией, опре­деляется законом Фика в виде

(6.16)

/л т\ д^с Qd- ^Da)i_dl

Феноменологическая закономерность (6.16) является, таким об­разом, некоторым усредненным детерминированным отражением процесса, имеющего на самом деле ярко выраженный вероятностный характер. Благодаря подобным усреднениям, мы отказываемся от стохастического анализа процессов массопереноса на микроуровне, связанного с необходимостью использования статистической теории фильтрации (см. раздел 1.5.4).

Важно отметить, что дисперсия может идти не только вдоль направления фильтрационного потока (как мы до сих пор предполагали), но и в перпендикулярном к нему направлении¹, Такая — поперечная — дисперсия также подчиняется закону (6.16), но с иным коэффициентом D\ имеющим, подобно (6.15), вид

^D' =^D_M+⁶i'^v' (6.17)

геометрический параметр <5/ при поперечной дисперсии

примерно на порядок меньше, чем при продольной, хотя опытного материала по этому поводу очень мало.

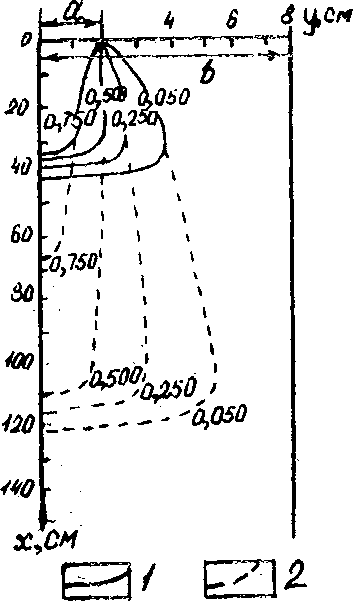
Значение поперечной дисперсии проще всего проил­люстрировать, запуская меченые частицы жидкости не по всей ширине, а лишь на ограниченном участке фильтра­ционного потока. Поперечная дисперсия приводит к рас­пространению меченых частиц за пределами зоны, огра­ниченной крайними траекториями фильтрации меченой жидкости, к появлению здесь переходных зон и *: умень­шению скоростей продвижения фронта вытеснения в продольном направлении. Все это хорошо иллюстрирует­ся рис. 6.8 [21], полученным по конкретному экспери­менту.

Слагаемые в формулах (6.15) и (6.17) отражают ин­тенсивность молекулярно-диффузионного и механиче­ского дисперсионного массопереноса: доля каждого из них в общем балансе массового потока определяется ско­ростью фильтрации v и структурой горных пород (для однородных пород — характерным размером минераль­ных зерен d₃). Так, из результатов лабораторных экспе­риментов следует, что при значениях vd₃, равных 0,0001 м²/сут и менее, доминирующей является молекулярная диффузия, а при значении vd₃, измеряемом сотыми - де­сятыми долями квадратных метров в сутки, резко преоб­ладает уже механическая дисперсия [21]. Грубо говоря, в

д с (с — с®) ционарный, то -*£j — —^л}

т.

М

( здесь т_ь —

И 1,

т.

На рис. 6.9 приведены два во­доносных пласта, разделенных слабопроницаемой толщей. В нижнем пласте, содержащем со­леную воду с текущей концентра­цией с, фильтрация практически отсутствует, а в верхнем пласте, интенсивно дренируемом рекой, поддерживается неизменная кон­центрация соли (Р. Напоры в обо­их пластах совпадают (перетека­ния нет), сорбцией соли в слабо­проницаемой толще пренебрега­ем. Требуется найти время полно­го рассоления нижнего пласта.

Выделим в рассматриваемом комплексе пород вертикальный столбик единичного поперечного сечения. Расход соли <? . выноси­мой из нижнего пласта олагодаря Рис. 6.8. Схема оценки совмест- молекулярной диффузии через ного влияния продольной и по- разделующую толщу, определим перечной дисперсии на распро- _По формуле (6.13) при (О. = 1. Ес- странение индикатора от ис- ¹

точника фиксированной длины: ^ли режим переноса соли квазиста-

породах глинистого состава обычно можно учитывать только молекулярную диффузию, в трещиноватых поро­дах — только механическую дисперсию, но в остальных случаях допустимость пренебрежения одной из составля­ющих диффузионно-дисперсионного рассеяния обычно требует более внимательного обоснования.

Со