1. Простейшие одномерные решения и пути

их использования для исследования двухмерных задач плановой фильтрации

1. Фундаментальное решение (задача о подпоре вблизи водохранилища)

Напорный водоносный пласт в прибрежной полосе водохранилища, урез воды в котором прямолинеен и про­стирается на большое расстояние в плане, представлен на рис. 4.2. Других границ пласта поблизости нет (схема полу ограниченного пласта). Считаем, что нам задано не­которое стационарное распределение исходных напоров в пласте Я/х). Пусть в момент (=0 уровень в водохрани­лище резко (условно-мгновенно) повышается на величи­ну А Я.°Требуется найти новое - нестационарное - распре­деление напоров для различных моментов времени t > 0.

Согласно зависимости (2.22а), исходное уравнение фильтрации имеет вид

*д²Н ^дН ^й дх² dt ’ (4.1)

где а — коэффициент пьезопроводности;

Я = Н(х, О;

ось х направлена нормально к урезу водохранилища.

Условие на левой границе пласта (при х = 0):

поп 1

московский 2

ДИНАМИКА ПОДЗЕМНЫХ 4

вод 4

О, = о_с-G„ =(Д„ — Д₀)(1 -n)-z=y,-z, 44

_/=^^а«.._с._й, ш 85

шшшш 145

^(4^)⁺f,(^r'5)^+£=°- 176

¹±шл ' 280

ДШш§ 443

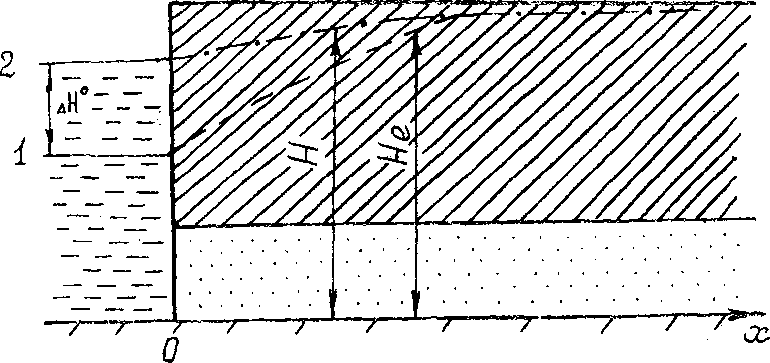
Рис. 4.2. Развитие подпора вблизи водохранилища;

1 - исходное положение пьезометрической кривой; 2 - текущее новое положение

Выражения (4.1)- (4.4) дают полную математическую постановку задачи. Однако их удобно предварительно упростить, введя новую функцию:

(4.5)

AH(x,t)=H(x,t)-H_e(x),

отвечающую изменению уровня в сечении х на момент t Тогда исходное уравнение принимает вид

* д

(4.6)

а

Ь(^АД>-эт<^АЯ>-

Л

ВОПРОС. Почему при переходе от уравнения (4.1) к (4.6) в

левой части пропал член

д\

дХ‘

? Напомним, что режим исходного

потока считается стационарным.

Краевые условия для функции АН выглядят заметно

проще:

AH(0,t) ~ АН°\ Д#(оо,*)=0; ДЯ(л;,0)=0.

АН

Введя функцию АН=——. преобразуем уравнение (4.6):

АН⁰

♦ а² (Ан) _д (Ah) ^a dx^{2 dt} (4.6a)

при краевых условиях

A77(0,f) = 1; А Доо,*) = О; А Дх,0) = 0 (4.7)

Отсюда следует, что безразмерная функция АТТзависит от двух аргументов: х q a t, имеющих размерность соответственно длины L и Lr: AH=*f(x, a t). Как следует из Я-теоремы (см. раздел 1.7), филь­трационный процесс в данном случае должен описываться функцио­нальной связью между двумя безразмерными комплексами, а это возможно лишь при условии, что А77=/(А), щеЯ — безразмерный комплекс, составленный из упомянутых аргументов. С учетом раз­мерности последних понятно, что структура величины А определя­ется общим выражением (Ах/VaT ) ^п, где Ann — константы.

Этот простейший пример демонстрирует, кстати, полезность привлечения теории подобия к анализу и решению дифференциаль­ных уравнений, приводимых к безразмерному виду: тем самым вы­являются общая структура решения и минимальное число перемен­ных, полностью характеризующих изучаемый процесс.

Для исследования поставленной краевой задачи (4.6)-(4.7) вве- дем теперь простейшую безразмерную комбинацию: А = л/(2 Vat)n попытаемся найти решение уравнения (4.6), зависящее только от А: АН=АДА). С этой целью заменим производные по t и по х произ­водными по новой переменной А:

£(ДН) =!(Д-*(ДЯ)£ (^) =

= -ж(^дд)^#7=-М(^дд)^;

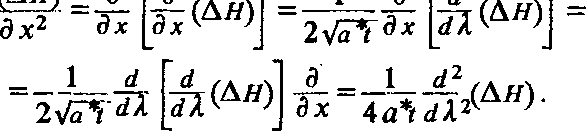
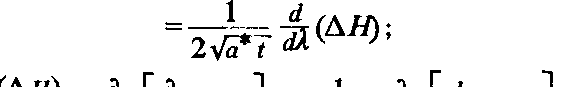
^(^Д/0=|(^ДЯ)М=|(^ДЙ)^ =

Подставляя полученные выражения в формулу (4.6), приходим к обыкновенному дифференциальному уравнению:

£|ЛЯ) ₊ 2А>Я)=0,

где Д#зависит только от одной переменной А, Введем и = =^(ДЯ); тогда

ff+2b=0-

уравнение с разделяющимися переменными:

— = -2А<*А.

и

Интегрируя, получаем

In См = —А^

где С — произвольная постоянная.

Переходя от функции и вновь к функции АН, имеем:

[Дя(А)] = .

Разделим переменные и проинтегрируем в пределах от А до <»:

СДя(А)|*=^ е~^ dz,

где под знаком определенного интеграла в правой части мы ввели новое обозначение z для переменной интегрирования (чтобы отли­чить ее от значения А нижнего предела интегрирования). Но условие А -* оо отвечает значению х -* оо, и, согласно второму из краевых условий (4.7), АН И-*00 “0. Поэтому последнее равенство упро­щается:

°о _ 2

СДя(А) = -/б *dz.

^{к }} О (4.9)

Для определения постоянной С воспользуемся значением АН при А = 0, т.е. при х *» 0. Тогда согласно первому из краевых условий (4.7) имеем

⁰⁰ —A

САЯ--fe -т d_z.

о

Определенный интеграл в этом равенстве — табличный, значе­ние его равно V$t72~ [16 J. Следовательно,

2 Дя⁰’

и решение (4.9) принимает вид

ML-A l -2 _й

г— J б uZ «

ДЯ° Я (4.10)

Функция, стоящая в правой части этого равенства и зависящая от нижнего предела интегрирования А, широко используется в раз­личных приложениях математики и физики. Для ее определения составлены подробные графики и таблицы (см. приложение 1), в которых она обозначается символом erfс\

о ⁰⁰ -У²

erfc(X)=~fe ^z dz.

wa (4.11)

Заметим, что erfc{<») = 0, a erfciO) ¹ 1.

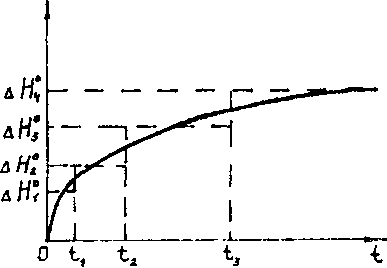
Решение (4.12) имеет фундаментальный характер. На его основе могут быть получены решения и для более сложных краевых условий. Если, например, график изме­нения уровня в водохранишище носит криволинейный

характер (рис. 4.3), то, аппроксимируя кривую Д H\t) серией мгновенных (ступенчатых) изменений напора, легко приходим к формулам для значений Д Я, отвечаю­щих каждому временному интервалу; так, для второго интервала (t₁ <t < t₂) получаем

AH = AH°erfc

<4.12)

X '

С учетом введенного обозначения решение постав­ленной задачи принимает окончательный вид:

АН = АН" erf с yU ₊д Щег/с

\ / \ ^{У 0/} /

аНЧЬ)

(4.13)

Тем самым использу­ется принцип сложения течений (см. раздел 3.3) : считается, что при t > t₁ продолжает развиваться возмущение, обусловлен- ное первым скачком уровня на границе, а с мо­мента времени t=t₁ к нему добавляется возмущение,

обусловленное вторым р_ис ^ j Аппроксимация кривой скачком. Для любого мо- изменения уровня мента t_n_j < t <t_n анало­гично имеем

(4.14)

А Н(х_у 0 ⁼ 2 A H?erfc / = 1

Из приведенных решений нетрудно найти выражения для удельного расхода потока, идущего от водохранили­ща. Например, для фундаментальной задачи

q (x,t) ~~т(АЯ) - Т-

дН л ^{д н}-

дх

д х

-о д _

^ " (4.15)

где q_e

- удельный расход естественного потока, направ­ленного в сторону водохранилища.

Используя формулу дифференцирования интеграла по переменному пределу, получаем

д , , _n d , , dl d (2 f -t , \ 1

Ti^{{erfcЯ) =} dl^(ефЩ{^{е dz}) 7477 ~

=_1 е-л² у5га*Т

Тогда

^q ^ ^t>~^q‘‘ ⁽⁴¹⁶>

ВОПРОС. Почему, согласно формуле (4.16), расход потока ока­зывается переменным не только во времени, но и в пространстве (сравните с аналогичной формулой (3.4) для стационарного движе­ния)?

На урезе водохранилища, т.е. для х — 0, при исходном горизонтальном уровне подземных вод

ТАН⁰

^q~tfхаТ ^<417)

Формула (4.17) внешне подобна формуле (3.4) для напорного стационарного потока, если ввести обозначе­ние

\6га* t =L, (4.18)

где переменная во времени величина L(t), имеющая раз­мерность длины, может рассматриваться как фиктивная (расчетная) длина нестационарного потока, при которой обеспечивается тот же расход на границе пласта, что и в стационарных условиях (при одинаковых перепадах на­поров на длине L).

В самом деле, при нестационарном движении частицам жидко­сти, находящимся на различных начальных удалениях от контура возмущения, приходится пробегать по пласту пути разной длины; поэтому, по аналогии с (3.53), величина Ф(t) * L(t)lT может рас­сматриваться как усредненное фильтрационное сопротивление воз­мущенного участка пласта, переменное во времени.

ЗАМЕЧАНИЕ. Иногда величину L(t) называют длиной области влияния инженерного сооружения (в данном случае — водохранили­ща) . Нужно, однако, отдавать себе отчет в нечеткости такого назва­ния, так как оно предполагает отсутствие возмущения на участках x^Lft). На самом же деле это не так: например, при x=I/t), т.е. при

Л ⁼~2~> изменение напора АН составляет около 20% от величины АН?

ВОПРОС. Из формулы (4.12) следует, что возмущение, обус­ловленное изменением напора на границе, фиксируется уже через коротки^ интервалы времени на сколь угодно большом расстоянии от границы . Чем объясняется этот физически нереальный результат? (для ответа вспомните замечание о силах инерции при рассмотрении закона Дарси).

Заметим, что полученное решение легко распростра­няется и на случай безнапорного пласта — посредством подстановки (2.38) или (2.38а). Например, для схемы безнапорного двухслойного пласта справедливы те же формулы (4.12) и (4.16) при замене в них а на коэффи­циент уровнепроводности, определяемый по формуле (2.35).

В целом полученное решение фундаментальной зада­чи не только имеет важное теоретическое значение, но и представляет широкий практический интерес. Оно ис­пользуется для расчета подпора грунтовых вод при запол­нении водохранилищ, для оценки притоков к дренажным траншеям или фильтрационных потерь из каналов, для определения коэффициента пьезопроводности по данным наблюдений за изменением уровней подземных вод вбли­зи рек и водоемов.

ЗАДАЧА. В паводковый период уровень воды в прибрежном пье­зометре резко повысился на 2 м. Через пять суток подъем уровня в наблюдательной скважине, удаленной от реки на 100 м, составил 30 см. Определить коэффициент уровнепроводности водоносного пла­ста.

При плавном подъеме паводкового уровня расчет коэффициента уровнепроводности ведется подбором по формуле (4.14) или с ис­пользованием характерных участков графика изменения уровня (по участку постоянной скорости подъема или по точке максимума). Последний из упомянутых способов предпочтителен, когда на подъ­ем уровня в реке накладывается усиление инфильтрационного пита­ния в пределах долины реки. Наряду с оценкой коэффициента уров- непроводности далее можно провести оценку параметра сопротивле­ния ложа реки AL(в разделе 3.4 аналогичная задача решалась нами в стационарной постановке). Для этого используются данные пьезо­метра, расположенного вблизи реки: по известному коэффициенту уровнепроводности с помощью решения (4.14) определяется теоре­тическое изменение уровня Л//^ и сопоставляется с замеренным

АН. Очевидно, разница в значениях этих величин обусловлен до­полнительным сопротивлением ложа реки. Отсюда из балансовых соображений нетрудно получить зависимость для определения AL.

ВОПРОС. Почему подобный подход к определению параметра AL оказывается мало надежным?