1. Задача о фильтрации к скважине в круговом пласте

^7^/777/7X7777,

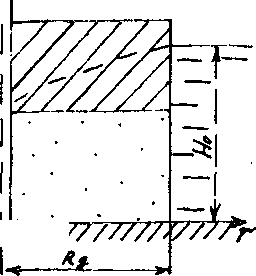
На рис. 3.8 по­казана скважина, откачивающая воду с постоян­ным расходом Q_c и расположенная в центре круглого острова, по всей площади которо­го распространен

Рис. 3.8. Схема напорной фильтрации к изолированный скважине в круговом пласте однородный на­

порный пласт.

ВОПРОС. Чем вызвана столь идеализированная постановка за­дачи? Почему, например, не сместить скважину относительно цент­ра острова?

Вода из бассейна поступает в скважину по радиальным траекториям, т.е. движение носит одномерный характер (зависит от одной координаты г).

Уравнение (2.20а), с учетом выражения (2.11) для оператора Лапласа в плоскорадиальном случае приводит к исходному дифференциальному уравнению:

dH

а / ап\ _л

7r(^rW>=⁰’

(3.27) где Н * Н(г).

Граничные условия с учетом формулы (2.45) имеют

вид

гг (п \ — IS dH I

V д) о; dr Iг-г_с 2 71'Т'Г_С ’ (3.28)

где г_с — радиус скважины.

Решение:

[Т] интегрируем уравнение (3.27) по г:

dH _п ^r4F^=C''

разделяем переменные и еще раз интегрируем:

<Я/=С, —,

1 _г

с Q-.

¹ 2 л-7”

dH — Cj In г + С₂ — общее решение уравнения; используем граничные условия:

н₀ = б-l 1» R, + с₂;

Q_c

С,

In Я,

2п-Т-г'

^С2 ^Яо 2яТ

а

подставляем Cj и С₂ в общее решение:

Qr г Н (г) = In ~ + Я₀ —

^w 2л-Т R_d ⁰ (3.29)

искомое решение задачи (пьезометрическая кривая явля­ется логарифмической линией). В частности, напор на контуре скважины

Q ^г

H,.=Tr^~ln-i£- +н_а,

' 2 л-Т Я_д (3,30)

т.е. формулу для Н(г) можно записать также в виде

Я(г) = Yjff^1пг ~ ^{1п г}о^+Нс~ 2л Т^{1п г + С} ’

(3.31)

где С зависит от условий на скважине. Последнее выраже­ние дает наиболее общую структуру решения задач пло­скорадиальной фильтрации вблизи скважин, работающих с постоянным расходом; оно удовлетворяет и уравнению

27. , и второму граничному условию в (3.28).

Если, наоборот, скважина работает в режиме заданно­го напора Н_с, то из формулы (3.30) получаем

_л _2яТ(Я₀-Я_с)_27tT S_c

^Qc In (Л/^Гс) In (^RAc) ’ (3.32)

где S_C⁼=H₀ — H_c — понижение напора в скважине.

ЗАДАЧА. Найти аналитическое выражение для оценки зависи­мости скорости фильтрации от расстояния до скважины.

Подстановкой (2.38а) получаем аналог последней формулы для безнапорного режима движения:

In (R_s /г_с) (3.33)

выражение, известное как формула Дюпюи для скважи­ны. Для этой формулы можно повторить все, что говори­лось о формуле Дюпюи и о промежутке высачивания в плоскопалаллельном случае (см. раздел 3.1.3).

ЗАМЕЧАНИЕ. Для реальных скважин дополнительный разрыв уровней на стенке скважины может быть обуслов­лен сопротивлением фильтра. Этот фактор мы пока не рассматриваем.

ВОПРОС. Почему приведенные здесь формулы нельзя исполь­зовать для расчета работы скважины в неограниченном пласте, когда вокруг скважины образуется круговая зона влияния радиуса №