5. Основной закон фильтрации и проницаемость горных пород

   1. Закон Дарси

Термином «фильтрация» охватывается движение жидкости в насыщенной ею пористой среде, обусловлен­ное наличием гидравлического градиента (перепада напо­ров).

Проведем следующий простейший эксперимент. Будем сначала пропускать воду через трубку длиной I с поперечным сечением со, заполненную песком, добиваясь при заданном перепаде напород на краях трубки А 7/постоянного расхода жидкости Q. Средняя скорость движения жидкости по порам:

_v - Q

0 0)‘П’ (1.47)

где п — эффективная пористость песка.

Рассчитаем теперь по формуле Гагена-Пуазейля (см. раздел 1.1.5) среднюю скорость течения v_d' в круглой трубке с поперечным

сечением ft)' =0)П Сопоставление v_d и v_&' покажет, что уже для трубок диаметром в несколько сантиметров v_& « v^', причем разни­ца в скоростях растет с увеличением поперечного сеченця трубы. Более того, значение v_d от размеров этого сечения не зависит. Следо­вательно, при одинаковых суммарных поперечных сечениях потока (ft)' =(л)'П) сопротивление движению воды в трубке, заполненной песком, многократно возрастает.

Обдумывая этот эксперимент, мы можем теперь вернуться к понятию пора: изложенное позволяет определить поры как такие пустоты, для которых сопротивление движению жидкости обуслов­лено главным образом силами трения жидкости об их стенки и при­стеночными эффектами. Очевидно, такое определение дает основа-

ние распространить термин «фильтрация» и на трещиноватые горные породы — если движение жидкости в них также характеризуется доминирующим значением сил трения жидкости о стенки.

Будучи частным случаем движения вязкой жидкости, фильтра­ция описывается общими уравнениями Навье-Стокса [17 J, которые являются отправным элементом анализа вязких течений в классиче­ской гидромеханике: в основе такого анализа лежит интегрирование этих уравнений при определенных краевых условиях. Однако с са­мого начала было ясно, что ввиду доминирующей роли пристеночных (пограничных) эффектов в сочетании с исключительно сложной ге­ометрией порового пространства, решение уравнений Навье-Стокса для пористой или трещиноватой среды является задачей практически неосуществимой. Этот путь, естественно, был закрыт для построения теории фильтрации и, в частности, для теоретического приближения к основному закону движения подземных вод на базе физически обоснованных упрощений. Однако приведенные выше (см. раздел 1.1) общие соображения о движении вязкой жидкости оказываются все-таки полезными для априорной характеристики такого закона.

Во-первых, основной закон движения должен отразить связь между силами сопротивления и изменениями энергии потока. Как следует из априорных энергетических представлений, приведенных в разделе 1.1, это эквивалентно установлению связей между измене­нием величины гидростатического напора и работой сил внутреннего трения на одной и той же длине А /, отсчитываемой вдоль линии тока; иначе говоря, можно ожидать наличия функциональной (линейной)

ЛЯ

связи между величинами -ду и силами внутреннего трения. Так,

подобно изложенному в разделе 1.1.4, нетрудно показать, что для пористой среды, представленной системой капилляров, справедлива формула, аналогичная (1.20)

_ Дя Ыр )ж“Д7> (1.48)

^гД^е Уж =Рж'&

р_ж — плотность жидкости;

/тр ~ ^силы трения, приходящиеся на единицу объема пористой среды.

Во-вторых, можно ожидать, что связь между средней скоростью движения жидкости в порах v_& и градиентом давления или напора

-ду будет носить линейный характер (движение ламинарное).

В-третьих, наконец, можно предположить, что для идеализиро­ванной пористой среды, представленной системой параллельных ка­пилляров радиуса г _у справедлива следующая зависимость, вытека­ющая из формулы Гагена-Пуазейля (1.18):

(1.49)

^Q 8 Я, Д/ ’

где Q — суммарный расход N капилляров.

Так как для единичного поперечного сечения Q - v_& п (см. формулу (1.47)), а N ———г-, то получаем отсюда ожидаемую

(¹•#

структуру основного закона фильтрации в следующем виде:

_ %'Рж Дя ^V»~^BH(1.50)

_Й-^Г" где ^B Y'

Проводя опыты по фильтрации воды в трубах, запол­ненных песком, А.Дарси установил (1856 г.), что резуль­таты этих опытов дают в координатах Ц +/ четко выра­женный прямолинейный график (рис. 1.21):

%^=к1> (1.51)

где а)— площадь поперечного сечения трубы;

к — коэффициент пропорциональности, постоянный для данного опыта, точнее — для данной пары грунт-жидкость.

Отношение расхода жидкости ко всему поперечному сечению фильтрующей горной породы

£

ш^=ху (1.52)

получило название скорости фильтрации. Эта расчет­ная величина более удобна на практике, чем действитель­ная средняя скорость движения воды в порах v_d, так как

она соотносится с легко замеряемым общим объемом гор­ной породы: согласно формулы (1.47), очевидна связь:

(1.53)

v = v_d-n

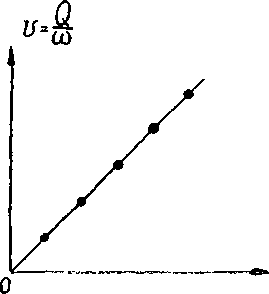
Рис. 1.21. График зависи­мости скорости фильт­рации от градиента

ЗАМЕЧАНИЕ. С учетом требова­ний, вытекающих из предпосылки сплошности среды, более корректное определение скорости фильтрации да­ется формулой

^Д^юс|'

где 0)_о — минимальная репрезентатив­ная площадка.

форме:

Вводя в закон Дарси (1.51) скорость фильтрации, перепи­шем его в дифференциальной

(1.54)

дН

' Ы

v = -к

или в проекциях на координатные оси,

дН

дх

дН

ду

дН

dz

v_x = -k

v_y = -k

(1.55)

у_г = -к

Такая форма записи позволяет утверждать, что вектор скорости фильтрации v связан со скалярным полем функции Н: вектор v в каждой точке (х у_п z ) направлен по нормали к поверхности Н -

С/у C/j Сf

const, проходящей через эту точку, причем

где grad# —вектор-градиент функции #, т.е. вектор, координаты которого равны соответственно и -^у.

Переписывая формулу (1.56) в виде

v=grad (—£•#), (1.57)

приходим к выводу, что функция (р — — к'Н является потенциалом для вектора скорости фильтрации — согласно известным положени­ям теории поля [ 16 ].

Если свойства среды, задаваемые коэффициентом к, в разных направлениях различны и определяются состав­ляющими к_х к_у k_z, то для такой анизотропной среды¹:

= _ ь iJf. IK. и ^дН

^v* ^X'dx'²y ^ky’dy'^{Vz z} dz ’ (1.58)

В дальнейшем опыты в фильтрационных трубах неод­нократно проводились с различными жидкостями и зако­ну Дарси был придан более общий вид:

^kQP*g дН ^V Рж 31 ' (1.59)

где коэффициент пропорциональности к₀ зависит толь­ко от свойств пористой среды.

Закон Дарси, подтвержденный многочисленными эксперимен­тами [6, 10, 36], является по своей сути эмпирическим законом; строгое теоретическое доказательство его справедливости, несмотря на многочисленные попытки такого рода, отсутствует . Однако тот факт, что структура формулы (1.59) идентична выражению (1.50), полученному теоретическим анализом течения в системе капилляр­ных трубок, позволяет относиться к закону Дарси с большим довери­ем.

В работе [46 ] изучалась модель течения в среде, состоящей из набора шаров одинаковыхразмеров. Решая уравнения Навье-Стокса для этой модели численным методом (на ЭВМ), авторы показали, что закон Дарси дает для нее погрешность менее 1 %.

До сих пор мы говорили о законе фильтрации в пори­стых средах, очевидно, трещины в горных породах как водопроводящие пути имеют мало общего (по своей гео­метрии) с порами. Однако из сформулированных выше представлений становится ясно, что в тех трещиноватых породах, где скорость движения жидкости по трещинам определяется (в первую очередь и в основном) силами трения жидкости о стенки и пристеночными эффектами, должен быть также справедливым закон Дарси.

Здесь полезно привести известную формулу Буссинеска, соглас­но которой при сравнительно малых числах Рейнольдса средняя ско­рость Vj течения жидкости по щели шириной Ь с параллельными гладкими стенками подчиняется линейной зависимости:

*^д~ ⁷‘ (1.60)

Если среднее расстояние между параллельными трещинами в горной породе равно 1_т, то ее пустотность (аналог пористости) п = Ь/1_т, и с учетом формулы (1.53) имеем для скорости фильтрации в системе параллельных гладких трещин формулу

Ъ²'Р_Ж'8 дН

дТ (1.60а)

Сопоставление этой формулы с выражением (1.59) подтвержда­ет их аналогию. Конечно, приведенное представление фильтрующих трещин в горной породе является существенной идеализацией; одна­ко опытный материал убедительно подтверждает, что и в реальных трещиноватых породах закон Дарси чаще всего выполняется с высо­кой степенью точности [6, 36 ].