2. Упругая емкость

Рассмотрим водоносную линзу в песках, окруженных относи­тельно водоупорными глинами. При вскрытии линзы скважиной фиксируется некоторый напор — вода в скважине устанавливается над верхней границей линзы. Откачивая из скважины воду, можно убедиться, что напорный уровень, постепенно понижаясь, будет еще довольно длительное время располагаться выше кровли линзы; пески при этом остаются полностью водонасыщенными, т.е. их гравитаци­онная емкостьы не проявляется. Кроме того, приток воды к линзе со стороны исключен. Естественно, напрашивается вопрос, откуда же берется вода, откачиваемая скважиной?

На основании примера, рассчитанного нами в разделе

1. и из сказанного в разделе 1.3 мы уже догадываемся, что напорный водоносный комплекс может отдавать воду двумя путями [36, 43]:

|Т~] за счет сжатия породы при приложении к ней дополнительных эффективных напряжений или, что в какой-то степени эквивалентно, при уменьшении нейт­

рал

ьных напряжений (см. раздел 1.3);

за счет расширения воды при уменьшении в ней гидростатического давления (см. раздел 1.1.1).

Оба эти механизма, определяющие упругую ем­кость водоносного комплекса, проявляются и в приведен­ном примере с линзой — при снижении напоров, обуслов­ленном откачкой. Рассмотрим более подробно их количе­ственную сторону. Для этого будем изучать поведение элементарного столбика (с единичной площадью попе­речного сечения) в напорном пласте мощностью т, огра­ниченном водоупорами сверху и снизу (рис. 1.18). Вес жидкости в столбике G —у₀'П'т\ исследуем его изменение

iF.

dG = dy₀'(n-m) +y₀'d‘(ti‘m)

J-JL

(1.32)

при снижении напора в пласте на величину I dH\ — — dH, причем, со­гласно изложенному в раз­деле 1.3,

ТУ

^~Г7-7-77^7-7^7!

ТУ

7~Т~Г7

Рис. 1.18. Схема к оценке упругой емкости пласта

do_u - do₀

JTJ К __ э

Го У О ’ (1.33)

где do₃ и do_H — соответственно приращения эффектив­ного и нейтрального напряжений, условно связанные с изменением напора dH через величину объемного веса жидкости у₀.

Согласно закону Гука для воды (1.1)

л ^уо _А dy_n =-j~r‘do

° ^Е0 (1.34)

При сжатии породы под дополнительными нагрузка­ми объем ее уменьшается главным образом за счет пор и трещин, так как сами минеральные зерна сжимаются очень слабо. Показателем интенсивности уменьшения объема пор по мере нагружения служит коэффици­ент сжимаемости а_с, равный изменению коэффициента пористости е, деленному на то приращение эффективного напряжения, которое привело к этому изменению:

_ de

^Ип ’ (1.35)

где е = ^ (см. раздел 1.2.1). £

Для определения коэффици­ента сжимаемости порезультатам испытаний образцов горных по­род строится график зависимости е —f (оJ, называемый компресси­онной кривой (рис. 1.19); уклон графика отвечает коэффициенту сжимаемости. Характерные зна- ⁰ ~ ~*б>

чения параметра а_с (в МПа'¹) для

песков « 10'³ -КО'²; ДЛЯ ГЛИН « Рис. 1.19. Компрессион- 0,01-Ю,1. В трещиноватых поро- ?*™^{мпрессион}-

дах сжимаемость трещинного

3 4 1

пространства отвечает значениям *» 10' -*-10' МПа' , но сжимаемость пористых блоков можетбыть большей на один-два порядка.

Выражение для изменения коэффициента пористости можно представить в виде

de — d'

п \		тп	d-(m'n)
1 —п \		т-( 1 —п)	~ т-( 1 - п) ’ (1.36)

где т (1 — п) — объем минерального скелета в выделен­ном столбике, считающийся неизменным (минеральные зерна практически несжи­маемы) .

Объединяя выражения (1.32) - (1.36), получаем

dG -у₀'ГП'П

•do.

(1.37)

'i <0

^Е,^{+ е}

\ ^в

Запишем теперь выражение для относительного изме­нения объема воды V в рассматриваемом объеме породы V_n, имея в виду, что V₀ = nV_n и do_H = у₀ dH:

ii

dV„ tidV.

Е. ^£

/

1 +£

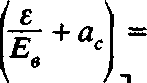
где

о __ dG_

У п _G п

*

V =

'do_H — rj 'dH,

(1.38)

*

П

(1.39)

Уо

g + (1 п)'й_с

Величина rj, называемая коэффициентом упругоем- кости горной породы [36], представляет сооой, таким образом, изменение объема жидкости в единице объема породы при единичном изменении напора. При снижении напора (dH < 0) количество жидкости в пласте уменьша­ется, т.е. каждая единица объема породы отдает объем воды, равный rj I dH I; соответственно с единицы площа-

ди пласта освобождается объем воды dV# равный 77**m \dH\, или

£Z?= *

dH Р (1.40)

где величина

—г] -т (1.41)

аналогична по смыслу коэффициенту гравитационной во­доотдачи (см. формулу 1.31)) и называется коэффициен­том упругой водоотдачи пласта.

Обратим внимание, что, как и параметр_/а, величина/г* безраз-

♦

мерна, в то время как коэффициент у^ругоемкости rj имеет размер­ность, обратную длине (например, м~ ).

В выражение (1.39) для коэффициента упругоемко- сти входят два слагаемых, первой из которых отражает роль упругих деформаций воды, а второе — сжимаемость горной породы. С учетом приведенных ранее характер­ных значений а_с и Е_в нетрудно показать, что первое сла­гаемое имеет смысл принимать во внимание лишь в чисто трещиноватых породах; во всех остальных случаях доми­нирующим источником упругих запасов воды в пласте служит уменьшение объема порового пространства, обусловленное ростом эффективных напряжений при снижении напоров.

В целом абсолютные значения коэффициентов упру-

гоемкости 77* невелики (вм¹): (0,5*5) • 10'⁴ —для песков; 10'⁴* 10"³ — для супесей и суглинков; 10 -НО" — для чисто трещиноватых пород (увеличиваясь примерно на порядок для типичных трещиновато-пористых пород - песчаников, известняков). Следовательно, при реальных мощностях водоносных горизонтов (метры, десятки мет­ров) значения коэффициента упругой водоотдачи на один-два порядка меньше коэффициентов гравитацион­ной емкости для тех же пород. Поэтому в безнапорных горизонтах, в которых при снижении уровней проявляют­ся и гравитационные, и упругие запасы, последними

обычно пренебрегают, т.е. считают fi «ju.

Однако в суглинистых и глинистых грунтах, а также в

некоторых трещиновато-пористых породах значения/г и /г различаются не столь сильно. Попутно заметим, что, как ясно из только что приведенных величин коэффици­ентов упругоемкости, упругая водоотдача «водоупорных» пластов глинистого состава может оказаться заметно большей, чем у смежных водоносных пластов.

■* 1 —> ^1 ~

Рис. 1.20. Схематическая колонка нижней пачки осадочных пород Южно- Белозерского месторож­дения:

1 - породы кристаллического фундамента; 2 - органогенные известняки мощностью 30 м; 3 - бучакские пески мощностью 15 м; 4 - киевские глины мощ­ностью 30 м

н

Последнее замечание касается не только глинистых водоупоров. Для при­мера рассмотрим разрез Южно-Белозер- ского железорудного месторождения (рис. 1.20). Здесь основные водоносные породы — бучакские п^ски — имеют проницаемость в 10 +10 раз большую, чем у подстилающих их пород — органо­генных известняков; поэтому известня­ки в прогнозах водопритоков принима­лись за относительный водоупор. В даль­нейшем оказалось, что водопонижаю­щие скважины, оборудованные на пес­ки, откачивали большей частью воду, поступавшую в пески из меловых пород.

ЗАДАЧА. Объясните описанный эф­фект количественно, принимая следую­щие исходные данные: коэффициент сжимаемости песков примерно раввд 0,005 МПа , известняков—0,03 МПа ; мощность песков 15 м, известняков 30 м. Снижение напоров в песках и в рудной толще (залегающей под известняками) составило Около 200 м.

При росте напоров в водонос­ном пласте (например, при нагне­тании воды) имеют место проти­воположные эффекты — упругое расширение порового простран­ства (декомпрессия горной поро­ды) и гидростатическое сжатие

поровой жидкости. В результате водоносный пласт при­нимает некоторое дополнительное количествоводы; соот­ветствующая емкость пласта — на единицу его площади — характеризуется коэффициентом недостатка (упру­гого) насыщения. Величина его для многих пород, одна­ко, заметно меньше, чем коэффициент упругой водоотда­чи. Обусловлено это тем, что сжимаемость ряда пород (особенно песчано-глинистых) при приложении допол­нительной нагрузки (р_э = у₀ I dH I) существенно больше

обратных деформаций упругого расширения при снятии нагрузки той же абсолютной величины. На опытном гра­фике сжимаемости (см. рис. 1.19) это обстоятельство от­ражается меньшим уклоном кривой декомпрессии в срав­нении с уклоном компрессионной кривой (компрессион­ный гистерезис). Однако при многократном нагружении- разгружении, характерном для различных циклических колебаний напоров подземных вод, подобные гистерезис- ные явления в емкостных свойствах не играют практиче­ской роли.

Рассмотрим проявление упругого режима при колебаниях ат­мосферного давления, вызывающих, как известно, изменения уров­ней в колодцах и открытых пьезометрах.

ЗАДАЧА. Прежде чем читать последующий материал попытай­тесь объяснить, почему перед грозой уровень воды в глубоких колод­цах заметно повышается?

При рассмотрении этого эффекта следует учесть, что в данном случае имеет место изменение полного напряжения О_п, вызванное

колебаниями атмосферного давления Р; так как dO_n — dP_a, то равен­ство (1.28) приводит к формуле

^d°_H ~ ^dPа ⁼ ~ ^йоэ• (1.42)

Кроме того, суммарное изменение давления столба воды в сква­жине (при изменении уровня на величину dh) и атмосферного дав­ления уравновешивается изменением гидростатического давления водоносного пласта, т.е.

y₀-dh + dP_a-dO_H. ₍₁.43)

Введем понятие барометрической эффективности BE как отно­шение изменения уровня воды в пьезометре dh к соответствующему изменению атмосферного давления в метрах водяного столба [42 ]:

_BE=_Jh ₌ dO_H-dP_a dO, ₌ _ 1

dP/Yo ^dPa dO_H+dO, 1 + do/dO_;

a .44)

Но из закона Гука для объема воды V_Q в единичном столбике

пласта (V_Q = пт) имеем

do = -Е -^ = -Е -й1члй

Н У_{0 п}-_т

или, с учетом выражений (1.35) и (1.36),

поп 1

московский 2

ДИНАМИКА ПОДЗЕМНЫХ 4

вод 4

О, = о_с-G„ =(Д„ — Д₀)(1 -n)-z=y,-z, 44

_/=^^а«.._с._й, ш 85

шшшш 145

^(4^)⁺f,(^r'5)^+£=°- 176

¹±шл ' 280

ДШш§ 443

т.е. увеличение атмосферного давления вызывает падение уровня в колодце или пьезометре тем большее, чем меньше сжимаемость по­род. Например, для грунтовых потоков в песках при £* 0,8 и о«0,05 МПа¹ I BE I < 0,01, в то время как для глубокозалегающих (200+300 м) напорных песчаных пластов при * 0,002 МПа" и Е * 0,5 I ВЕ\ >0,1. Следовательно, перед грозой, при падении атмосферного давления на 2 кПа, уровень воды в скважине, пройденной на напор­ный пласт, поднимается на несколько сантиметров.

В заключение остается заметить, что, как и в случае гравитационной емкости, коэффициент упругой водоот­дачи считается не зависящим от времени протекания про­цесса: в исходных зависимостях (1.34) и (1.35) деформа­ции предполагались идущими синхронно с изменением напоров в пласте. В разделе 5.3 мы убедимся, что в неко­торых комплексах пород это допущение справедливо лишь для достаточно длительных процессов.

Итак, в этом разделое мы ввели важные гидрогеоло­гические параметры, характеризующие емкостные свойства водоносной системы — коэффициенты гравита­ционной и упругой водоотдачи. Данными параметрами определяются запасы воды в геологических структурах и поэтому их оценке уделяется особое внимание при гидро­геологических изысканиях. Об этой стороне дела мы по­говорим в гл. 5, пока же — в последующих разделах мы будем предполагать параметры емкости заданными ха­рактеристиками изучаемых гидродинамических процес­сов.