2.1.2 Приведенное напряжение для продольных стыков крыла

Регулярными зонами крыла, долговечность которых определяет долговечность конструкции крыла, являются продольные стыки, к которым можно отнести:

- стыки панелей;

- стыки панелей с поясами лонжеронов;

- стыки стенок с поясами лонжеронов.

На рисунке 9.8 приведен эскиз продольного стыка панелей при помощи стыкового профиля.

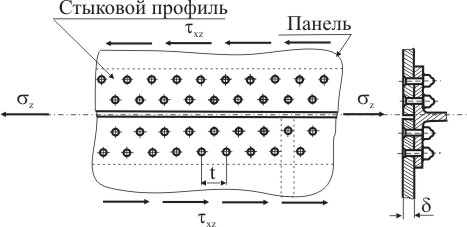
Рисунок 9.8

Выделим прямоугольный элемент из панели в окрестрости отверстия для крепежного элемента. По граням выделенного элемента будут действовать нормальные напряжения σ_z, касательные напряжения τ_xz, и усилие P_б, действующее на контур отверстия от крепежного элемента. Используя принцип суперпозиции представим нагруженное состояние в окрестности отверстия в виде двух, одно из которых преставляет нагружение отверстия нормальными напряжениями σ_z, а второе нагружение касательными напряжениями τ_xz и уравновешивающим усилием P_б, действующим на контур отверстия (рис. 9.9).

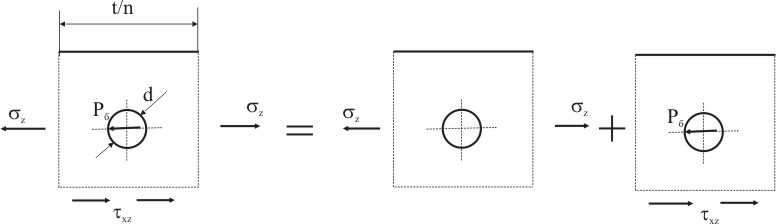
Рисунок 9.9

В результате концентрации на контуре отверстия возникает повышенное напряжение σ_к э, которое можно определить как сумму наибольших напряжений на контуре для двух состояний:

, где (5)

- коэффициенты концентрации от нормальных напряжений и напряжений смятия;

σ_z – нормальные напряжения;

σ_см – напряжения смятия.

Напряжение смятия определяется усилием на крепежный элемент P_б толщиной панели в зоне крепежного отверстия δ и диаметром крепежного отверстия d:

При равномерном распределении усилий по крепежным элементам усилие на болт P_б определяется шагом крепежных отверстий t, числом крепежных элементов на одном шаге n, толщиной панели δ и величиной касательных напряжений τ_xz:

С достаточной степенью точности для реальных соединений и условий нагружения .

Тогда соотношение (5) после подстановок можно преобразовать к виду:

(6)

В случае одноосного нагружения образца с отверстием напряжением σ_прив на контуре отверстия в точке возможного зарождения усталостной трещины возникает σ_к о:

(7)

Приравняем правые части соотношений (6) и (7), и после преобразований получим, что приведенное напряжение равно:

2.1.3 Приведенное напряжение для поперечных стыков

К наиболее часто встречающимся поперечным стыкам верхних и нижних панелей крыла можно отнести:

- поперечные стыки панелей центроплана с панелями консольной части крыла;

- поперечные стыки панелей консольной части крыла с панелями отъемной части крыла.

В конструкции гермофюзеляжа к поперечным стыкам можно отнести:

- продольные (относительно оси фюзеляжа) стыки обшивки фюзеляжа, выполняемые обычно внахлест;

- поперечные (относительно оси фюзеляжа) соединения, выполняемые обычно встык по накладке.

На рисунке 9.10 приведен эскиз поперечного стыка панелей при помощи стыковой накладки с шагом крепежных элементов t и числом крепежных элементов на одном шаге n.

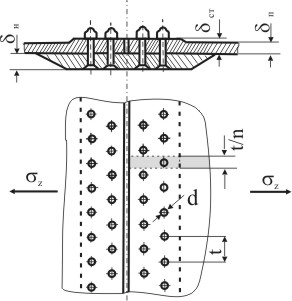
Рисунок 9.10

Выделим прямоугольный элемент из панели в окрестности отверстия для крепежного элемента шириной t/n (рис.9.11а). По граням выделенного элемента будут действовать усилие P_п на подходе к отверстию и усилие P_ст после отверстия. Кроме того на контур отверстия будет действовать усилием P_б.

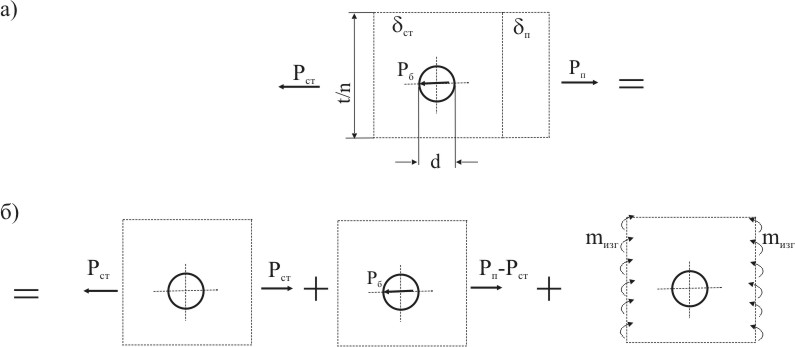
Рисунок 9.11

Используя принцип суперпозиции, представим нагруженное состояние в окрестности отверстия в виде трех, одно из которых преставляет осевое растяжение усилием P_ст, второе осевым усилием P_п -P_ст и уравновешивающим усилием P_б, действующим на контур отверстия, а третье нагружение распределенными изгибающими моментами m_изг, вызванными несоосной передачей усилия с панели на стыковую накладку (рис. 9.11б).

Определим усилие, передаваемое панелью на одном шаге P_п:

При равномерном распределении усилий по крепежным элементам усилие на болт P_б определяется соотношением:

Определим усилие, проходящее за крепежным элементом P_ст:

Для определения изгибающих моментов m_изг рассмотрим расчетную схему стыка, приведенную на рисунке 9.12. Определим изгибающий момент в сечении по первому ряду крепежных элементов в предположении, что между накладкой и панелью отсутсвует проскальзывание.

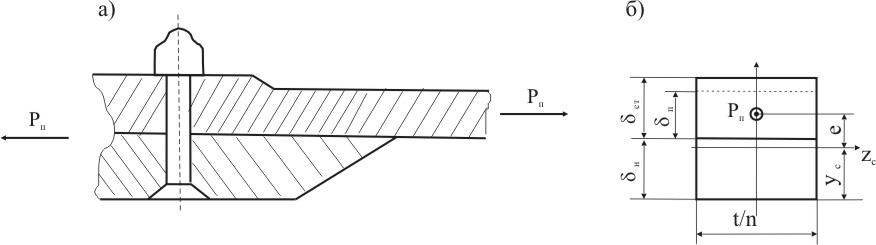
Рисунок 9.12

Так как, рассматриваемое сечение (рис. 9.12б) находится в условиях внецентренного растяжения, то изгибающий момент будет равен:

m_z=P×e, где

e- расстояние между равнодействующей P и главной центральной осью сечения z_c;

P- усилие в панели на единице ширины.

Учитывая, что и что равнодействующая P приложена в середине толщины панели в случае равномерного распределения напряжений по её толщине, тогда из рисунка 9.12б:

Определим усилие в панели на единице ширины:

P=_z×_п

После подстановок, распределенный изгибающий момент будет равен:

В результате концентрации на контуре отверстия возникает повышенное напряжение σ_к э, которое можно определить как сумму наибольших напряжений на контуре для трех состояний:

, где (8)

- коэффициенты концентрации от нормальных напряжений, напряжений смятия и изгибных напряжений;

σ_z – нормальные напряжения;

σ_см – напряжения смятия;

σ_изг – напряжения локального изгиба;

n- число крепежных элементов на одном шаге.

Напряжение смятия определяется усилием на крепежный элемент P_б толщиной панели в зоне крепежного отверстия δ и диаметром крепежного отверстия d:

При равномерном распределении усилий по крепежным элементам усилие на болт P_б определяется шагом крепежных отверстий t, числом крепежных элементов на одном шаге n, толщиной панели δ и величиной нормальных напряжений, которое действует за первым крепежным элементом :

С достаточной степенью точности для реальных соединений и условий нагружения . Экспериментальными исследованиями установлено, что . Примем, что , тогда соотношение (8) после подстановок можно преобразовать к виду:

(6)

В случае одноосного нагружения образца с отверстием напряжением σ_прив на контуре отверстия в точке возможного зарождения усталостной трещины возникает σ_к о:

(7)

Приравняем правые части соотношений (6) и (7), и после преобразований получим, что приведенное напряжение равно: