Историческая справка
Методы определения перемещений в стержневых системах основаны на принципе возможных перемещений, который был, вероятно, впервые, распространен на деформируемые тела С. Пуассоном в 1833 г. В этом случае он формулируется следующим образом: из всех возможных состояний равновесию системы, подверженной воздействию внешних сил, соответствует то, при котором полная энергия системы принимает стационарное значение. Использование этого вариационного принципа позволяет вывести теорему Ж. Лагранжа, согласно которой для линейных систем частная производная от потенциальной энергии деформации по обобщенному перемещению равна соответствующей ему обобщенной силе. Вероятно, эту теорему было бы правильнее называть первой теоремой Коттерилла‑Кастильяно по именам Д. Коттерилла и А. Кастильяно. Д. Коттерилл еще до Кастильяно в 1865 г. опубликовал четыре работы, в которых установил сформулированную выше теорему, а также теорему о том, что для линейных систем частная производная от потенциальной энергии деформации по обобщенной силе равна соответствующему этой силе обобщенному перемещению. В курсах сопротивления материалов эта теорема обычно называется теоремой Кастильяно, который доказал ее в дипломной работе, посвященной расчету ферм в Туринском политехническом институте в 1873 г. и опубликовал полученный результат на итальянском языке в 1875 г., а на французском‑в 1879 г.
Полученные результаты были использованы Кастильяно для определения лишних неизвестных в статически неопределимых фермах, а в дальнейшем обобщены им на упругое тело произвольной формы. Заметим, что еще до Кастильяно в 1857 г. Л. Менабреа, занимаясь расчетами статически неопределимых ферм, предложил определять лишние неизвестные, исходя из минимума потенциальной энергии деформации. Это положение получило название начала наименьшей работы. Статья Л. Менабреа на итальянском языке была опубликована в 1857 г., а на французском‑в 1858 г. Однако обоснование этого начала Менабреа не дал. Очевидно, что оно следует из второй теоремы Коттерилла—Кастильяно.
Из второй теоремы Коттерилла—Кастильяно обычно выводится очень удобная формула для определения перемещений в стержневых системах‑интеграл перемещений, который в курсах сопротивления материалов обычно называется интегралом Мора. Этот метод определения перемещений опубликован О. Мором в ряде статей в 1874 г. Для частного случая определения перемещений в фермах этот способ был предложен раньше в 1864 г. Д. Максвеллом. Поэтому интеграл перемещений следовало бы, вероятно, назвать интегралом Максвелла—Мора. Интеграл Максвелла—Мора для прямого стержня постоянного по перечного сечения может быть вычислен при помощи простого правила, предложенного А.К. Верещагиным в бытность им студентом Московского института инженеров транспорта в 1924 г.
1. Типы стержневых систем
Стержневыми системами принято называть конструкции, элементы которых имеют форму плоского или пространственного бруса.
Стержневая система называется плоской, если оси всех составляющих ее брусьев расположены в одной плоскости и в этой же плоскости расположены все внешние нагрузки и одна из двух главных центральных осей инерции всех поперечных сечений системы. Такая система будет деформироваться только в своей плоскости. Системы, в которых указанные условия не соблюдены, называются пространственными. Геометрически плоская система с нагрузкой, перпендикулярной этой плоскости, называется плоскопространственной.
Конструкции из прямых стержней, испытывающих, главным образом, растяжение или сжатие, называются фермами. В фермах нагрузки прикладываются к ее узлам, а соединение стержней в узлах ферм считается идеально шарнирным. Стержни фермы выполняются в виде тонких длинных брусьев с малой изгибной и крутильной жесткостью.
Стержневые системы, элементы которых работают главным образом на изгиб и кручение, называются рамами. Для рам характерно жесткое соединение составляющих их брусьев в узлах. Жестким считается соединение, при котором в процессе деформации брусьев углы между их осями в вершинах узлов не изменяются (рис. 7.1).
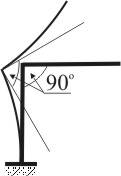
Рисунок 7.1
Отдельные части рамы могут быть соединены шарнирно. Соотношение продольных и поперечных размеров составляющих раму брусьев подбирается так, чтобы их изгибные EI и крутильные GJ жесткости были достаточно большими. Системы, содержащие одновременно элементы рамного и ферменного типа, а иногда и пружины, называются смешанными.