3.3. Формула Ясинского-Тетмайера для определения критических напряжений

Применение подхода Кармана на практике требует знание диаграммы деформирования “σ‑ε” для материала стержня сжатия, что осложняет ее применение. Поэтому для определения критических напряжений, превышающих предел пропорциональности, предпочитают пользоваться либо непосредственно экспериментальными данными, либо эмпирическими формулами. Наибольшее распространение получила линейная зависимость предположения Ясинским-Тетмайером:

σ_кр = a - bλ.

Зная σ_кр можно определить критическую нагрузку: P_кр = σ_кр F, где F - площадь сечения.

Формула справедлива для стержней средней гибкости, для которых гибкость находится в пределах λ₀ ≤ λ≤ λ_пред. Для коротких стержней малой гибкости, у которых λ < λ₀ величина критических напряжений равна предельному напряжению сжатия (пределу текучести σ_{т сж} для пластичных материалов, либо пределу прочности σ_{в сж} для хрупких материалов).

Для стержней большой гибкости λ> λ_пред расчет ведется по формуле Эйлера, поэтому зависимость σ_кр от λ гиперболическая: _кр= .

Изобразим графически зависимость критического напряжения _кр от гибкости λ (рис. 6.17).

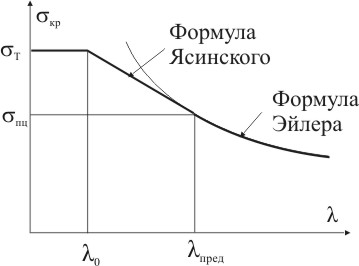
Рисунок 6.17

Для стержней малой гибкости зависимость «σ_кр –λ» выражена горизонтальной прямой, для стержней средней гибкости - наклонной прямой, а для стержней большой гибкости – гиперболой Эйлера. Четкой границы между стержнями малой и средней гибкости провести невозможно. В расчетах принимают λ₀ ≈ (0,2-0,4)λ_пред. Выбрав λ₀ можно найти коэффициенты a и b в формуле Ясинского σ_кр = a + bλ, составляя уравнение прямой проходящей через две точки с координатами (λ₀, _{т сж}) и (λ_пред, _пц):

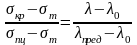
Значения a и b для некоторых материалов приведены в таблице 6.3.

Таблица 6.3

№	Материал	a, Н/мм2	b, Н/мм2	0	пред
1	Сталь Ст.2	264	0,7	60	105
2	Сталь Ст.3	310	1,14	60	100
3	Стали Ст.4, Ст.20	328	1,15	60	96
4	Сталь Ст.45	449	1,67	52	85
5	Дуралюмин Д-16	406	1,83	30	53

Глава 7. Статически определимые стержневые системы

В различного рода конструкциях (подмоторных рамах подвески двигателей, шасси, пространственных конструкциях крепления корпусов, отсеков) часто используют статически определимые стержневые системы. Основным свойством статически определимой стержневой системы является то, что она содержит минимально достаточное количество, как опорных элементов, так и достаточное число стержней, чтобы быть геометрически неизменяемой при действии нагрузки. Это означает, что при удалении хоть одного опорного элемента, или стержня из системы, система превращается в механизм и не может воспринимать действие нагрузки.

Стержневые системы являются статически определимыми, если усилия во всех сечениях их элементов и опорные реакции могут быть найдены из одних лишь уравнений равновесия.