2. Осевые, центробежный и полярный моменты инерции плоских сечений

В прямоугольной системе координат рассматривают осевые и центробежные моменты инерции. Осевым моментом инерции плоского сечения относительно относительно координатной оси называют интеграл по всей площади сечения от произведения площади элементарной площадки dF на квадрат расстояния до рассматриваемой оси z или y:

,

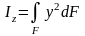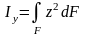
Центробежным моментом инерции плоского сечения называют интеграл по всей площади сечения от произведения площади элементарной площадки dF на расстояния до двух взаимно перпендикулярных осей z и у:

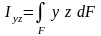
В полярной системе координат, определяют полярный момент инерции, который выражается интегралом вида:

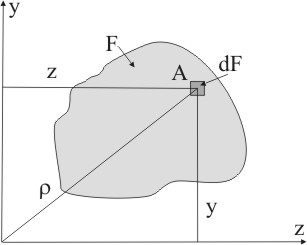
Рисунок 5.3

Рассматривая рисунок 5.3 можно заметить:

ρ² = z² + y²

Подставим это выражение в I_p:

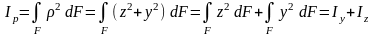
Таким образом, сумма осевых моментов инерции плоского сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения осей.

3. Изменение моментов инерции при параллельном переносе осей

Определим, как изменяется моменты инерции сечения, относительно оси параллельной центральной. Зададимся моментами инерции сечения относительно центральных осей z_c и у_c, проходящими через центр тяжести сечения I_zc, I_yc, I_yczc.

Проведем оси z и y параллельно центральным z_c и y_c на расстоянии y_c и z_c (рис. 5.4) и запишем выражение осевого момента инерции относительно оси z :

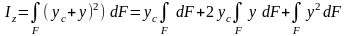
По определению, ,

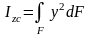Т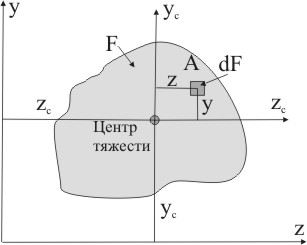 ак как ось z_c - центральная, то S_zc = 0.

Рисунок 5.4

Окончательно получим:

I_z= I_zc + y_c² F, аналогично:

I_y= I_yc + z_c² F, I_zy= I_zcyc + z_c  y_c F

4. Изменение моментов инерции при повороте осей координат

П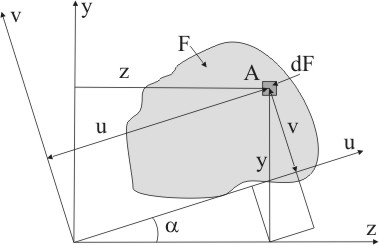 редположим, что для поперечного сечения произвольной формы известны моменты инерции относительно осей z, y прямоугольной системы координат (не обязательно центральной) I_z, I_y, I_zy. Определим моменты инерции I_u, I_v, I_uv относительно осей u и v прямоугольной системы координат повернутой относительно исходной на угол α (рис. 5.5).

Рисунок 5.5

Из рисунка можно заметить, что координаты u и v связаны с координатами z и y соотношениями:

u = z  cos α+ y  sin α

v = y  cos α - z  sin α

Моменты инерции относительно осей u и v:

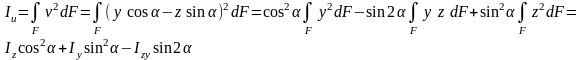
Аналогично, получим:

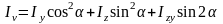
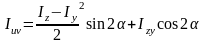
Учитывая, что:

,

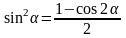
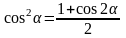полученные зависимости I_u, I_v, I_uv можно преобразовать к виду:

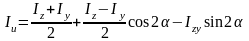
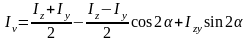
5. Главные оси и главные моменты инерции. Круг инерции Мора

Сложим, правые и левые части первых двух соотношений I_u и I_v, получим:

I_u + I_v = I_z + I_y

Это соотношение носит название инварианта момента инерции. Из него следует, что сумма осевых моментов инерции относительно любых двух взаимно ортогональных осей величина постоянная. Поэтому существует такое α, при котором один осевой момент достигает максимального значения, а другой осевой момент инерции относительно оси перпендикулярной первой оси принимает минимальное значение. Для определения этого значения α продифференцируем выражение I_u по α и приравняем производную нулю:

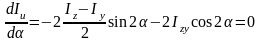, откуда:

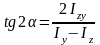
Приравняв нулю выражение I_uv,

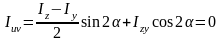получим:

Таким образом, существует один и тот же угол поворота осей координат α, относительно которых осевые центробежные моменты инерции I_u и I_v достигают экстремальных значений, а центробежный момент I_uv равен нулю.

Оси, относительно которых центробежный момент инерции равен нулю называют главными осями. Главные оси с началом координат, совпадающим с центром тяжести сечения, называют главными центральными осями.

Осевые моменты инерции относительно главных осей называют главными моментами инерции.

Для определения главных моментов инерции, подставим в I_u и I_v выражения:

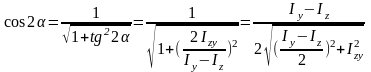
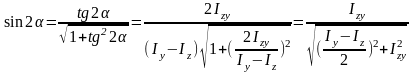
Окончательно, главные моменты инерции, которые принято обозначать I₁ и I₂:

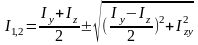
Полученные выражения I₁ и I₂ удобно представить в графическом виде кругом инерции Мора (рис.5.6).

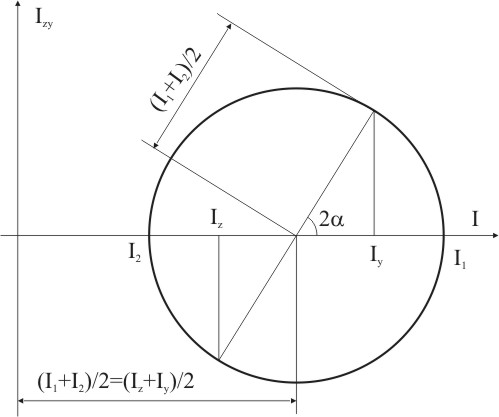
Рисунок 5.6

Отметим очень важное свойство. Если сечение имеет ось симметрии, то эта ось является главной осью. Это вызвано тем, что относительно оси симметрии центробежный момент инерции равен нулю, так как центробежный момент инерции части сечения, расположенный по одну сторону от оси инерции, равен моменту части расположенной по другую сторону, но противоположен по знаку.